Линейная независимость

Каждую строку матрицы А обозначим е_i= (a_i1a_i2…,a_in) (например, е₁= (a₁₁a₁₂…,a_1n), е₂= (a₂₁a₂₂…,a_2n) и т.д.). Каждая из них представляет собой матрицу-строку, которую можно умножить на число или сложить с другой строкой по общим правилам действий с матрицами.

Линейной комбинациейстрок e_l, e₂,...e_kназывают сумму произведений этих строк на произвольные действительные числа: e =_le_l+₂e₂+...+_ke_k, где_l,₂,...,_k- произвольные числа (коэффициенты линейной комбинации).

Строки матрицы e_l, e₂,...e_mназываютсялинейно зависимыми, если существуют такие числа_l,₂,...,_m, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:_le_l+₂e₂+...+_me_m= 0, где 0 = (0 0...0).

Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Действительно, пусть для определенности последний коэффициент _m0. Тогда, разделив обе части равенства на_m, получим выражение для последней строки, как линейной комбинации остальных строк: e_m= (_l/_m)e_l+ (₂/_m)e₂+...+ (_m-1/_m)e_m-1.

Если линейная комбинация строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю, т.е. _le_l+₂e₂+...+_me_m= 0_k= 0k, то строки называютлинейно независимыми.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые можно линейно выразить все остальные ее строки или столбцы.

Докажем эту теорему. Пусть матрица А размера m х n имеет ранг r (r(А)min{m;n}). Следовательно, существует отличный от нуля минор r-го порядка. Всякий такой минор будем называтьбазисным. Пусть для определенности это минор

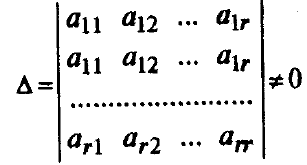
Строки этого минора также будем называть базисными.

Докажем, что тогда строки матрицы e_l, e₂,...e_rлинейно независимы. Предположим противное, т.е. одна из этих строк, напримерr-я, является линейной комбинацией остальных: e_r=_le_l+₂e₂+...+_r-1e_r-1= 0. Тогда, если вычесть из элементов r-й строки элементы 1-й строки, умноженные на_l, элементы 2-й строки, умноженные на₂, и т.д., наконец, элементы (r-1)-й строки, умноженные на_r-1, тоr-я строка станет нулевой. При этом по свойствам определителя вышеприведенный определитель не должен измениться, и при этом должен быть равен нулю. Получено противоречие, линейная независимость строк доказана.

Теперь докажем, что любые (r+1) строк матрицы линейно зависимы, т.е. любую строку можно выразить через базисные.

Дополним рассмотренный ранее минор еще одной строкой (i-й) и еще одним столбцом (j-м). В результате получим минор (r+1)-го порядка, который по определению ранга равен нулю:

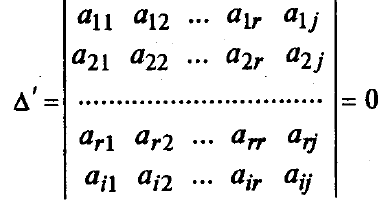
Разложим его по элементам j-го столбца. Здесь последнее алгебраическое дополнение А_ijсовпадает с базисным минором0А_ij0. Поэтому можно разделить обе части последнего равенства на А_ij. Это позволит выразить из него элемент:.

Если зафиксировать номер строки (i), то получим, что для любого j элементы i-й строки линейно выражаются через элементы базисных строк: , т.е. любая строка матрицы является линейной комбинацией базисных.

Теорема доказана.