Обратная матрица

Матрицу А^-1называютобратнойпо отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А^-1* А = А * А^-1= Е.

Из определения следует, что обратная матрица является квадратной матрицей того же порядка, что и матрица А.

Можно отметить, что понятие обратной матрицы аналогично понятию обратного числа (это число, которое при умножении на данное число дает единицу: а*а^-1= а*(1/а) = 1).

Все числа, кроме нуля, имеют обратные числа.

Чтобы решить вопрос о том, имеет ли квадратная матрица обратную, необходимо найти ее определитель. Если определитель матрицы равен нулю, то такая матрица называется вырожденной, илиособенной.

Необходимое и достаточное условие существования обратной матрицы: обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.

Докажем необходимость. Пусть матрица А имеет обратную матрицу А^-1, т.е. А^-1* А = Е. Тогда |А^-1* А| = |А^-1| * |А| = |Е| = 1. Следовательно, |А|0.

Докажем достаточность. Чтобы его доказать, необходимо просто описать способ вычисления обратной матрицы, который мы всегда сможем применить для невырожденной матрицы.

Итак, пусть |А| 0. Транспонируем матрицу А. Для каждого элемента А^Т найдем алгебраическое дополнение и составим из них матрицу, которую называютприсоединенной (взаимной, союзной):.

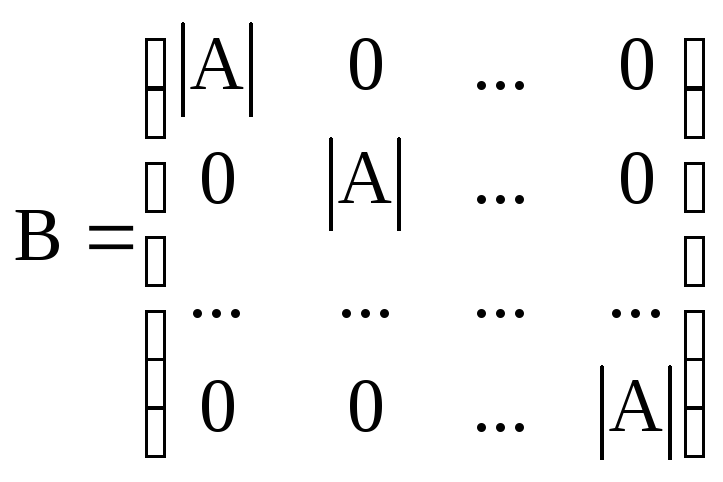
Найдем произведение присоединенной матрицы и исходной . Получим. Таким образом матрица В – диагональная. На ее главной диагонали стоят определители исходной матрицы, а все остальные элементы – нули:

Аналогично можно показать, что .

Если разделить все элементы матрицы на |А|, то будет получена единичная матрица Е.

Таким образом , т.е..

Докажем единственность обратной матрицы. Предположим, что существует другая обратная матрица для А, отличная от А^-1. Обозначим ее X. Тогда А * Х = Е. Умножим слева обе части равенства на А^-1.

А^-1* А * Х = А^-1* Е

Е * Х = А^-1

Х = А^-1

Единственность доказана.

Итак, алгоритм вычисления обратной матрицы состоит из следующих шагов:

1. Найти определитель матрицы |А| . Если |А| = 0, то матрица А - вырожденная, и обратную матрицу найти нельзя. Если |А| 0, то переходят к следующему шагу.

2. Построить транспонированную матрицу А^Т.

3. Найти алгебраические дополнения элементов транспонированной матрицы и построить присоединенную матрицу .

4. Вычислить обратную матрицу, разделив присоединенную матрицу на |А|.

5. Можно проверить правильность вычисления обратной матрицы в соответствии с определением: А^-1* А = А * А^-1= Е.

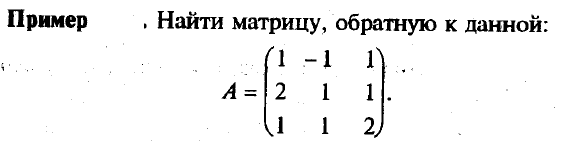
1. Найдем определитель этой матрицы по правилу треугольников:

 0.

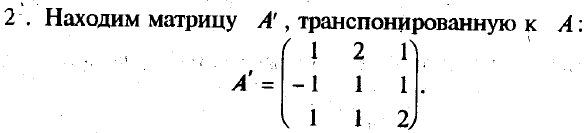
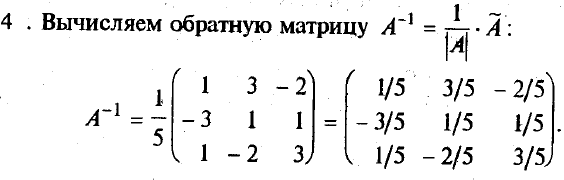
Проверку опустим.

Можно доказать следующие свойства обращения матриц:

1) |А^-1| = 1/|А|

2) (А^-1)^-1= А

3) (А^m)^-1= (А^-1)^m

4) (АB)^-1=B^-1* А^-1

5) (А^-1)^T= (А^T)^-1

Ранг матрицы

Минором k-го порядкаматрицы А размера m х n называют определитель квадратной матрицыk-го порядка, которая получена из матрицы А вычеркиванием каких-либо строк и столбцов.

Из определения следует, что порядок минора не превосходит меньшего из ее размеров, т.е. kmin{m;n}. Например, из матрицы А_5х3можно получить квадратные подматрицы первого, второго и третьего порядков (соответственно, рассчитать миноры этих порядков).

Рангомматрицы называют наивысший порядок отличных от нуля миноров этой матрицы (обозначают rang А, илиr(А)).

Из определения следует, что

1) ранг матрицы не превосходит меньшего из ее размеров, т.е. r(А)min{m;n};

2) r(А) = 0 тогда и только тогда, когда матрица нулевая (все элементы матрицы равны нулю), т.е.r(А) = 0А = 0;

3) для квадратной матрицы n-го порядка r(А) = n тогда и только тогда, когда эта матрица А невырожденная, т.е.r(А) = n|А|0.

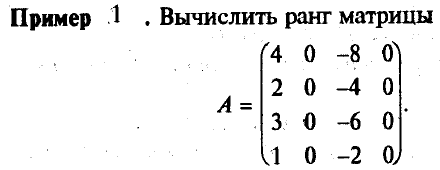
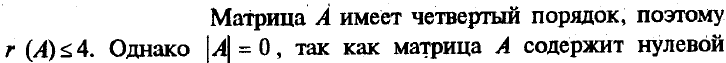
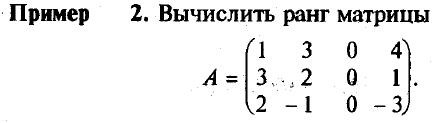
На самом деле, для этого достаточно вычислить только один такой минор (тот, который получен вычеркиванием третьего столбца (потому что в остальных будет присутствовать нулевой третий столбец, и поэтому они равны нулю).

По правилу треугольника 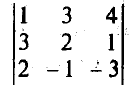= 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Поскольку все миноры третьего порядка нулевые, r(А)2. Так как существует ненулевой минор второго порядка, например,

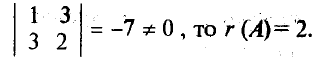
Очевидно, что использованные нами приемы (рассмотрение всевозможных миноров) не подходят для определения ранга в более сложных случаях ввиду большой трудоемкости. Обычно для нахождения ранга матрицы используют некоторые преобразования, которые называют элементарными:

1). Отбрасывание нулевых строк (столбцов).

2). Умножение всех элементов строки или столбца матрицы на число, отличное от нуля.

3). Изменение порядка строк (столбцов) матрицы.

4). Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5). Транспонирование.

Если матрица А получена из матрицы Bэлементарными преобразованиями, то эти матрицы называютэквивалентнымии обозначают АВ.

Теорема. Элементарные преобразования матрицы не изменяют ее ранг.

Доказательство теоремы следует из свойств определителя матрицы. В самом деле, при этих преобразованиях определители квадратных матриц либо сохраняются, либо умножаются на число, не равное нулю. В результате наивысший порядок отличных от нуля миноров исходной матрицы остается прежним, т.е. ее ранг не меняются.

С помощью элементарных преобразований матрицу приводят к так называемому ступенчатому виду (преобразуют в ступенчатую матрицу), т.е. добиваются, чтобы в эквивалентной матрице под главной диагональю стояли только нулевые элементы, а на главной диагонали – ненулевые:

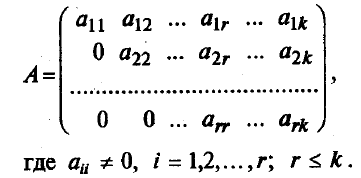
Ранг ступенчатой матрицы равен r, так как вычеркиванием из нее столбцов, начиная с (r + 1)-го и дальше можно получить треугольную матрицу r-го порядка, определитель которой будет отличен от нуля, так как будет представлять собой произведение ненулевых элементов (следовательно, имеется минор r-го порядка, не равный нулю):

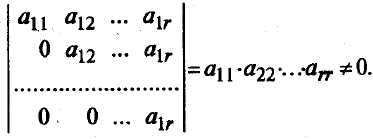
Пример. Найти ранг матрицы

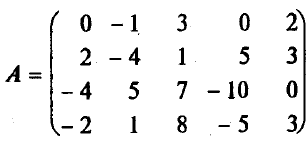
1). Если а₁₁= 0 (как в нашем случае), то перестановкой строк или столбцов добьемся того, чтобы а₁₁0. Здесь поменяем местами 1-ю и 2-ю строки матрицы:

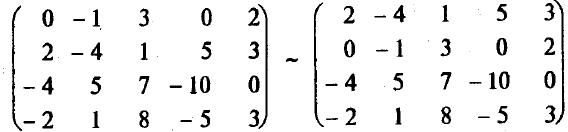
2). Теперь а₁₁0. Элементарными преобразованиями добьемся того, чтобы все остальные элементы в первом столбце равнялись нулю. Во второй строкеa₂₁= 0. В третьей строкеa₃₁= -4. Чтобы вместо (-4) стоял 0, прибавим к третьей строке первую строку, умноженную на 2 (т.е. на (-а₃₁/а₁₁) = -(-4)/2 = = 2). Аналогично к четвертой строке прибавим первую строку (умноженную на единицу, т.е. на (-а₄₁/а₁₁) = -(-2)/2 = 1).

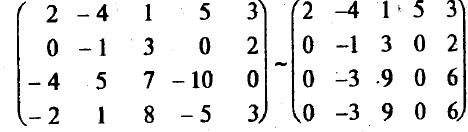
3). В полученной матрице а₂₂0 (если бы было а₂₂= 0, то можно было бы снова переставить строки). Добьемся, чтобы ниже диагонали во втором столбце тоже стояли нули. Для этого к 3-й и 4-й строкам прибавим вторую строку, умноженную на -3 ((-а₃₂/а₂₂) = (-а₄₂/а₂₂) = -(-3)/(-1) = -3):

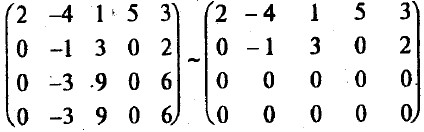
4). В полученной матрице две последние строки – нулевые, и их можно отбросить:

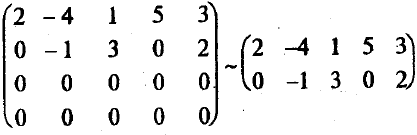
Получена ступенчатая матрица, состоящая из двух строк. Следовательно, r(A) = 2.