Геометрический и экономический смысл определенного интеграла

Из определения следует, что для неотрицательной функции f(x) определенный интегралравен площади криволинейной трапеции, ограниченной кривой у =f(x), прямыми х = а, х =bи осью абсциссy= 0 (рисунок 4.1).

Если функция – f(x) неположительна, то определенный интегралравен площади соответствующей криволинейной трапеции, взятой со знаком минус (рисунок 4.7).

Рисунок 4.7 – Геометрический смысл определенного интеграла для неположительной функции

Для произвольной непрерывной функции f(x) определенный интегралравен сумме площадей криволинейных трапеций, лежащих под графиком функцииf(x) и выше оси абсцисс, за вычетом суммы площадей криволинейных трапеций, лежащих над графиком функцииf(x) и ниже оси абсцисс (рисунок 4.8).

Рисунок 4.8 – Геометрический смысл определенного интеграла для произвольной непрерывной функции f(x) (знаком «плюс» помечена площадь, которую прибавляют, а «минусом» - та, которую вычитают).

При вычислении на практике площадей криволинейных фигур часто используется следующая формула: , гдеS– площадь фигуры, заключенной между кривыми y = f₁(x) и y = f₂(x) на отрезке [а,b], а f₁(x) и f₂(x) - непрерывные функции, заданные на этом отрезке, такие, что f₁(x) ≥ f₂(x) (см. рисунки 4.9, 4.10).

При изучении экономического смысла производной было выяснено, что производная выступает как скорость изменения некоторого экономического объекта или процесса во времени или относительного другого исследуемого фактора. Чтобы установить экономический смысл определенного интеграла, необходимо саму эту скорость рассмотреть в виде функции от времени или другого фактора. Тогда, так как определенный интеграл представляет собой изменение первообразной, мы получим, что в экономике он оценивает изменение этого объекта (процесса) за определенный период времени (или при определенном изменении другого фактора).

Например, если функция q=q(t) описывает производительность труда в зависимости от времени, то определенный интеграл от этой функциипредставляет собой объем выпущенной продукцииQза промежуток времени отt₀доt₁.

Методы вычисления определенных интеграловоснованы на рассмотренных ранее методах интегрирования (доказательств проводить не будем).

При нахождении неопределенного интеграла мы пользовались методом замены переменной, основанным на формуле: f(x)dx= =f((t))`(t)dt, где x =(t) - функция, дифференцируемая на рассматриваемом промежутке. Для определенного интеграла формула замены переменной примет вид, гдеи для всех.

Пример 1. Найти

Пусть t= 2 –x². Тогдаdt= -2xdxиxdx= - ½dt.

При х = 0 t= 2 – 0²= 2. При х = 1t= 2 – 1²= 1. Тогда

Пример 2. Найти

Пример 3. Найти

Формула интегрирования по частям для определенного интеграла примет вид:, где.

Пример 1. Найти

Пусть u=ln(1 +x),dv=dx. Тогда

Пример 2. Найти

Вычисление площадей плоских фигур с помощью определенного интеграла

Пример 1.Найти площадь фигуры, ограниченной линиями у = х²– 2 иy=x.

График функции y= х²– 2 представляет собой параболу с точкой минимума приx= 0,y= -2; ось абсцисс пересекается в точках. График функции у = х – прямая, биссектриса неотрицательной координатной четверти.

Найдем координаты точек пересечения параболы у = х²– 2 и прямой у = х, решив систему этих уравнений:

х²– 2 = х

х²– х - 2 = 0

Д = 1 + 8 = 9

х = 2; y= 2 или х = -1;y= -1

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.9.

Рисунок 4.9 – Фигура, ограниченная линиями у = х²– 2 иy=x

На отрезке [-1, 2] х ≥ х²– 2 .

Воспользуемся формулой , полагая f₁(х) = х; f₂(х) = х²– 2;a= -1;b= 2.

Пример 2.Найти площадь фигуры, ограниченной линиями у = 4 - х²иy= х²– 2x.

График функции y = 4 - х²представляет собой параболу с точкой максимума приx= 0,y= 4; ось абсцисс пересекается в точках 2 и -2. График функции у = х²– 2x– парабола с точкой минимума при 2x- 2 = 0, х = 1;y= -1; ось абсцисс пересекается в точках 0 и 2.

Найдем координаты точек пересечения кривых:

4 - х²= х²– 2х

2х²– 2х - 4 = 0

х²– х - 2 = 0

Д = 1 + 8 = 9

х = 2; y= 0 или х = -1;y= 3

Таким образом, фигуру, площадь которой необходимо найти, можно предствить на рисунке 4.10.

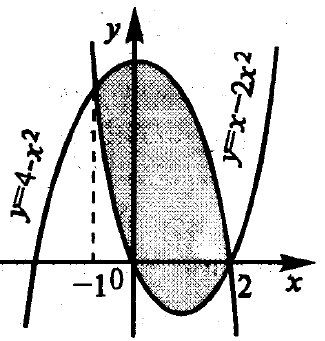
Рисунок 4.10 - Фигура, ограниченная линиями у = 4 - х²иy= х²– 2x

На отрезке [-1, 2] 4 - х²≥ х²– 2x.

Воспользуемся формулой , полагая f₁(х) = 4 - - х²; f₂(х) = х²– 2х;a= -1;b= 2.

Пример 3.Найти площадь фигуры, ограниченной линиями у = 1/х;y= х²иy= 4 в неотрицательной координатной четверти.

График функции у = 1/х представляет собой гиперболу, при положительных х она выпукла вниз; оси координат являются асимптотами. График функции у = х²в неотрицательной координатной четверти – ветвь параболы с точкой минимума в начале координат. Эти графики пересекаются при 1/х = х²; х³= 1; х = 1; у = 1.

Прямую y= 4 график функции у = 1/х пересекает при х =1/4, а график функции у = х²при х = 2 (или -2).

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.11.

Рисунок 4.11 - Фигура, ограниченная линиями у = 1/х; y= х²иy= 4 в неотрицательной координатной четверти

Искомая площадь фигуры ABCравна разности между площадью прямоугольника АВНЕ, которая равна 4*(2 – ¼) = 7, и суммой площадей двух криволинейных трапеций АСFЕ и СВНF. Вычислим площадь АСFЕ:

Вычислим площадь СВНF:

.

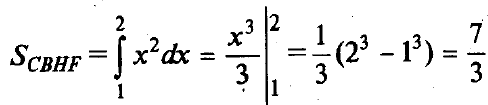Итак, искомая площадь равна 7 – (ln4 + 7/3) = 14/3 –ln43,28 (ед.²).