Список («таблица») основных интегралов

Перечислим интегралы от элементарных функций, которые иногда называют табличными:

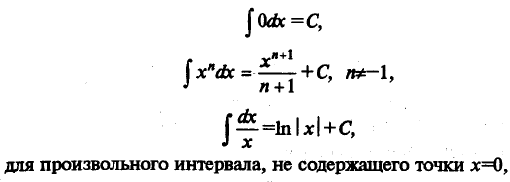
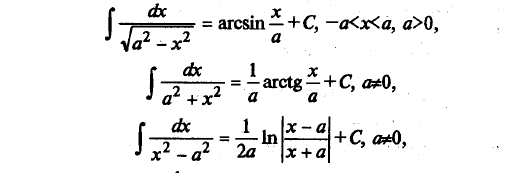
Любую из приведенных выше формул можно доказать, взяв производную от правой части (в результате будет получены подынтегральная функция).

Методы интегрирования

Рассмотрим некоторые основные методы интегрирования. К ним относятся:

1. Метод разложения (непосредственного интегрирования).

Этот метод основан на непосредственном применении табличных интегралов, а также на применении свойств 4 и 5 неопределенного интеграла (т.е. на выносе за скобку постоянного сомножителя и/или представления подынтегральной функции в виде суммы функций – разложения подынтегральной функции на слагаемые).

Пример 1.Например, для нахождения(dx/x⁴) можно непосредственно воспользоваться табличным интегралом дляxⁿdx. В самом деле,(dx/x⁴) =x^-4dx=x^-3/(-3) +C= -1/3x³+C.

Рассмотрим еще несколько примеров.

Пример 2. Для нахождениявоспользуемся тем же интегралом:

Пример 3. Для нахождениянадо взять

Пример 4. Чтобы найти, представим подынтегральную функцию в видеи используем табличный интеграл для показательной функции:

Рассмотрим использование выноса за скобку постоянного сомножителя.

Пример 5. Найдем, например. Учитывая, что , получим

Пример 6. Найдем. Поскольку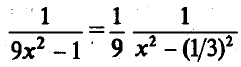, воспользуемся табличным интеграломПолучим

В следующих двух примерах также можно использовать вынос за скобки и табличные интегралы:

Пример 7.

(используем и);

Пример 8.

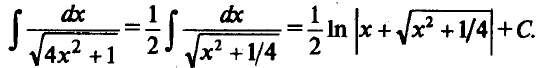
(используем и).

Рассмотрим более сложные примеры, в которых используется интеграл суммы.

Пример 9. Например, найдем. Для применения метода разложения в числителе используем формулу куба суммы^, а затем полученный многочлен почленно разделим на знаменатель.

=((8x^3/2+ 12x+ 6x^1/2+ 1)/(x^3/2))dx=(8 + 12x^-1/2+ 6/x+x^-3/2)dx= 8dx+ 12x^-1/2dx+ + 6dx/x+x^-3/2dx=

Следует отметить, что в конце решения записана одна общая постоянная С (а не отдельные при интегрировании каждого слагаемого). В дальнейшем также предлагается опускать в процессе решения постоянные от интегрирования отдельных слагаемых до тех пор, пока выражение содержит хотя бы один неопределенный интеграл (будем записывать одну постоянную в конце решения).

Пример 10. Найдем. Для решения этой задачи разложим на множители числитель (после этого удастся сократить знаменатель).

Пример 11. Найдем. Здесь можно использовать тригонометрические тождества.

Иногда, чтобы разложить выражение на слагаемые, приходится применять более сложные приемы.

Пример 12. Найдем. В подынтегральной функции выделим целую часть дроби. Тогда

.

Пример 13. Найдем

2. Метод замены переменной (метод подстановки)

Метод основан на следующей формуле: f(x)dx=f((t))`(t)dt, где x =(t) - функция, дифференцируемая на рассматриваемом промежутке.

Доказательство. Найдем производные по переменной tот левой и правой частей формулы.

Отметим, что в левой части находится сложная функция, промежуточным аргументом которой является x = (t). Поэтому, чтобы дифференцировать ее поt, сначала дифференцируем интеграл по x, а затем возмем производную от промежуточного аргумента поt.

( f(x)dx)`<sub>t</sub> = ( f(x)dx)`_x*x`<sub>t</sub> = f(x) `(t)

Производная от правой части:

(f((t))`(t)dt)`_t=f((t))`(t) =f(x)`(t)

Так как эти производные равны, по следствию из теоремы Лагранжа левая и правая части доказываемой формулы отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить. Доказано.

Удачная замена переменной позволяет упростить исходный интеграл, а в простейших случаях свести его к табличному. В применении этого метода различают методы линейной и нелинейной подстановки.

а) Метод линейной подстановкирассмотрим на примере.

Пример 1.. Пустьt= 1 – 2x, тогда

x= ½ - ½t

dx=d( ½ - ½t) = - ½dt

Следует отметить, что новую переменную можно не выписывать явно. В таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала, - т.е. о неявной замене переменной.

Пример 2.Например, найдемcos(3x + 2)dx. По свойствам дифференциала dx = (1/3)d(3x) = (1/3)d(3x + 2), тогдаcos(3x + 2)dx =(1/3)cos(3x + 2)d(3x + + 2) = (1/3)cos(3x + 2)d(3x + 2) = (1/3)sin(3x + 2) +C.

В обоих рассмотренных примерах для нахождения интегралов была использована линейная подстановка t=kx+b(k0).

В общем случае справедлива следующая теорема.

Теорема о линейной подстановке. ПустьF(х) - некоторая первообразная для функцииf(х). Тогдаf(kx+b)dx= (1/k)F(kx+b) +C, где k и b - некоторые постоянные,k0.

Доказательство.

По определению интеграла f(kx+b)d(kx+b) =F(kx+b) +C. Hod(kx+b)= (kx+b)`dx=kdx. Вынесем постоянный множительkза знак интеграла:kf(kx+b)dx=F(kx+b) +C. Теперь можно разделить левую и правую части равенства наkи получить доказываемое утверждение с точностью до обозначения постоянного слагаемого.

Данная теорема утверждает, что если в определение интеграла f(x)dx= F(x) + C вместо аргумента х подставить выражение (kx+b), то это приведет к появлению дополнительного множителя 1/kперед первообразной.

С использованием доказанной теоремы решим следующие примеры.

Пример 3.

Найдем . Здесьkx+b= 3 –x, т.е.k= -1,b= 3. Тогда

Пример 4.

Найдем. Здесьkx+b= 4x+ 3, т.е.k= 4,b= 3. Тогда

Пример 5.

Найдем . Здесьkx+b= -2x+ 7, т.е.k= -2,b= 7. Тогда

.

Пример 6. Найдем. Здесьkx+b= 2x+ 0, т.е.k= 2,b= 0.

.

Сравним полученный результат с примером 8, который был решен методом разложения. Решая эту же задачу другим методом, мы получили ответ . Сравним полученные результаты:. Таким образом, эти выражения отличаются друг от друга на постоянное слагаемое, т.е. полученные ответы не противоречат друг другу.

Пример 7. Найдем. Выделим в знаменателе полный квадрат.

В некоторых случаях замена переменной не сводит интеграл непосредственно к табличному, но может упростить решение, сделав возможным применение на последующем шаге метода разложения.

Пример 8. Например, найдем. Заменимt=x+ 2, тогдаdt=d(x+ 2) =dx. Тогда

,

где С = С₁– 6 (при подстановке вместоtвыражения (x+ 2) вместо первых двух слагаемых получим ½x²-2x– 6).

Пример 9. Найдем. Пустьt= 2x+ 1, тогдаdt= 2dx;dx= ½dt;x= (t– 1)/2.

Подставим вместо tвыражение (2x+ 1), раскроем скобки и приведем подобные.

Отметим, что в процессе преобразований мы перешли к другому постоянному слагаемому, т.к. группу постоянных слагаемых в процессе преобразований можно было опустить.

б) Метод нелинейной подстановкирассмотрим на примере.

Пример 1. . Пустьt= -x². Далее можно было бы выразить х черезt, затем найти выражение для dxи реализовать замену переменной в искомом интеграле. Но в данном случае проще поступить по-другому. Найдемdt=d(-x²) = -2xdx. Отметим, что выражениеxdxявляется сомножителем подынтегрального выражения искомого интеграла. Выразим его из полученного равенстваxdx= - ½dt. Тогда

=  (- ½)e^tdt = (- ½) e^tdt = (- ½)e^t + C = (- ½)+ C

Рассмотрим еще несколько примеров.

Пример 2. Найдем. Пустьt= 1 -x². Тогда

;

Пример 3. Найдем. Пустьt=. Тогда

;

Пример 4. В случае нелинейной подстановки также бывает удобно использовать неявную замену переменной.

Например, найдем . Запишемxdx= = (-1/4)d(3 - 2x²) (неявно заменили переменнойt= 3 - 2x²). Тогда

Пример 5. Найдем. Здесь тоже введем переменную под знак дифференциала:(неявная заменаt= 3 + 5x³). Тогда

Пример 6. Найдем. Поскольку,

.

Пример 7. Найдем. Поскольку, то

Рассмотрим несколько примеров, в которых возникает необходимость сочетать различные подстановки.

Пример 8. Найдем. Пустьt= 2x+ 1, тогдаx= (t– 1)/2;dx= ½dt.

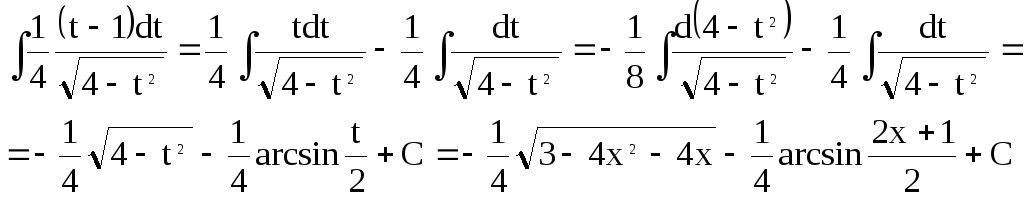
Пример 9. Найдем. Пустьt=x- 2, тогдаx=t+ 2;dx=dt.