
- •Минимальный остов
- •Другие названия
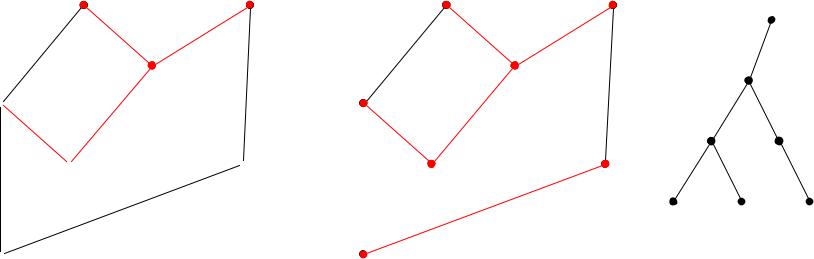
- •Пример КСС (Из «Кратчайшие связывающие сети и некоторые обобщения» - Р.К. Прим. //
- •e E w(e) 0 в V , E нет циклов
- •Принципы, лежащие в основе алгоритма построения минимального остова.
- •Принцип 1: Любая вершина соединяется с ближайшей (по весу ребра)
- •Использование матричной (табличной) записи для реализации алгоритма Прима.
- •Минимальный остов – простая задача

Минимальный остов
Постановка задачи
Исходные данные:
Связный граф с разметкой ребер весами
Цель:
Связный подграф с минимальной суммой весов ребер, включающий ВСЕ вершины исходного
Подграф: |
V V |
& E E |
Задача: |
min |
w(e) |
|
E E& |
|
|
|
e E |
|
V V |
|
|
|
|
G(V , E) & V V w RE
V V V V
Связность: ˆ V
Смежность:
{(x, y) |{x, y} E}
 V , E минимальный остов
V , E минимальный остов  V , E
V , E
Другие названия
Кратчайший остов (остовной подграф) Минимальное остовное дерево.
Минимальная (кратчайшая) связывающая сеть (КСС) англ: Shortest connection network – Prim R.C
Кратчайшее соединяющее (связующее) поддерево англ: Shortest Spanning Subtree – Kruskal J.B., Jr
SST |
(Shortest Skeleton Tree) |
Примеры:
Коммуникации, транспорт.
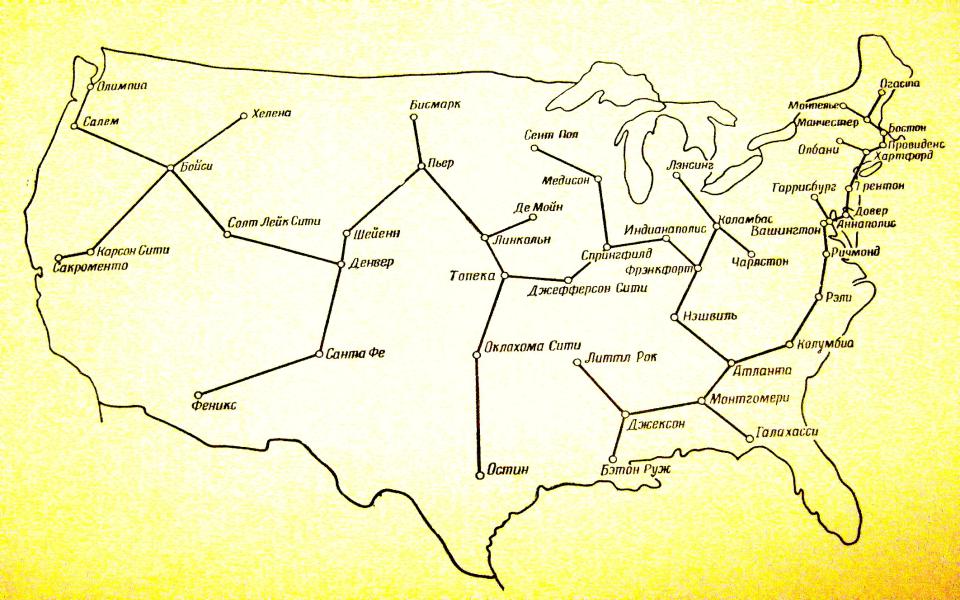
Пример КСС (Из «Кратчайшие связывающие сети и некоторые обобщения» - Р.К. Прим. // Кибернетический сборник №2. М: Издательство иностранной литературы, 1960)
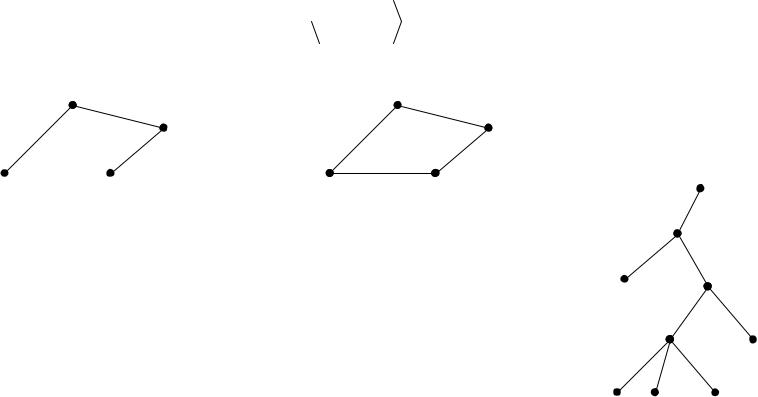
e E w(e) 0 в  V , E нет циклов
V , E нет циклов
w( ≤ w(
Связный граф без циклов – дерево
Минимальный остов – дерево (если e E w(e)≥0)

Принципы, лежащие в основе алгоритма построения минимального остова.
Начальное условие: |
V , |
|
множество изолированных |
||
|
||
вершин |
|
Фрагмент – связный подграф V′,E′ (поддерево) на этапе построения
E′ – ребра фрагмента.
′ – связность фрагмента.
Начальный фрагмент – любая одиночная вершина
V V & V V
V {v} v V
Весовое расстояние между фрагментом и внешней вершиной
v V \V |
|
d( V , E |
|
, v) min w({v, v }) |
|
|
|
v V |
|
||
|
|
|
|
|
|

Принцип 1: Любая вершина соединяется с ближайшей (по весу ребра) |
||||
смежной с ней вершиной в минимальном остове V,Emin . |
||||
v V |
& v V |
& ( v V |
w(v, v ) w(v, v )) |
{v, v } Emin |
Принцип 2: Любой изолированный фрагмент соединяется с ближайшей (по весовому расстоянию) к фрагменту вершиной минимальным по весу ребром.
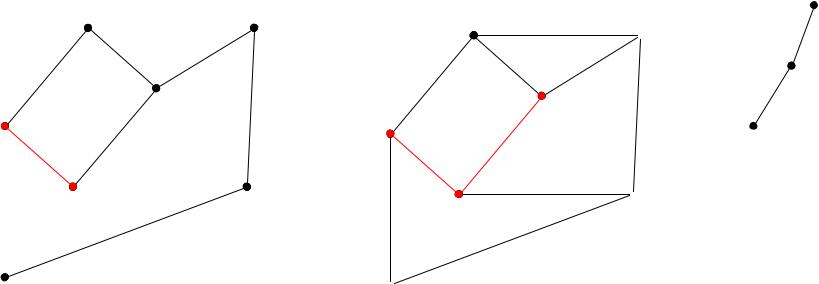
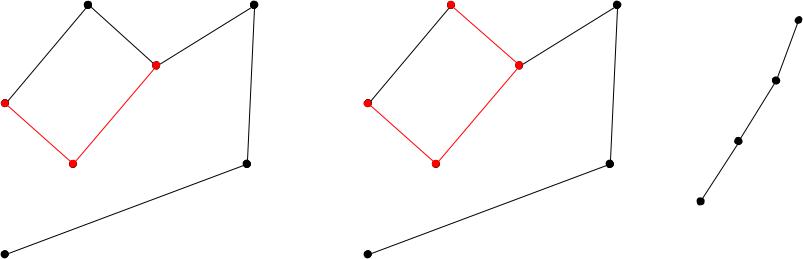
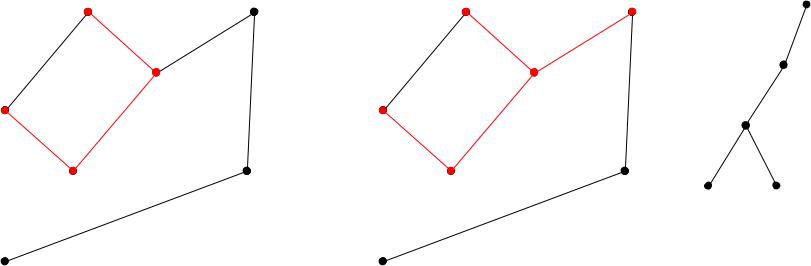
Шаг алгоритма (алгоритм Прима): V′,E′ V′′,E′′
(v V \V |
: v V \V |
|
d( V , E |
|
, v ) d( V , E |
|
, v)) |
||||||
|
|
|
|
: v V |
|
|
|
|
|
|
|||
& |
(v V |
|
|
|
w({v , v }) w({v, v })) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(V V {v } |
|
& E E {v , v }) |
|
|
|
|||||||
Т.е.: Выбрать ближайшую (по весовому расстоянию) к фрагменту вершину и соединить ее с фрагментом минимальным по весу ребром.
Шаги выполняются, пока фрагмент не покроет все вершины графа.
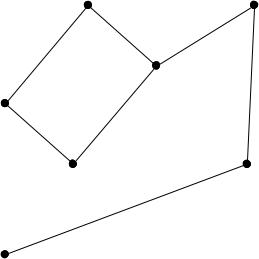
Использование матричной (табличной) записи для реализации алгоритма Прима.
V {v1, v2 , vn}
Матрица весов ребер (как в алгоритмах поиска маршрута)
|
|
W |
w({v , v |
}) |
||||
|
|
|
i j |
|
||||
|
|
ij |
0 |
|
|
|
|
|
|
2 |
6 |
3 |
|||||
|
3 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
4 |
|
|
5 |
|
|
2 |
|
2 |
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
|
|
6 |
8 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
,{vi , vj } E ,{vi , vj } E
0 |
3 |
0 |
0 |
2 |
0 |
8 |
|
|
3 |
0 |
6 |
1 |
0 |
0 |
0 |
|
|
6 |
0 |
4 |
0 |
5 |
|
0 |
0 |
||||||
|
|
|
|
|
2 |
0 |
|
W 0 1 4 0 |
0 |
||||||
|
2 |
0 |
0 |
2 |
0 |
4 |
0 |
|
|
0 |
5 |
0 |
4 |
0 |
|
0 |
3 |
||||||
|
|
0 |
0 |
0 |
0 |
3 |
|
8 |
0 |
||||||
|
|
|
|
|
|
min |
|
|
|
|
Фрагменту |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|||
0 3 0 0 |
2 |
0 |
8 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||
|
3 |
0 |
6 |
1 |
0 |
0 |
0 |
|
2=min({3,2,8}) 3 |
1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
4 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
6 |
0 |
4 |
0 |
5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
||||||||||
|
0 |
1 |
4 |
0 |
2 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
0 |
0 |
2 |
0 |
4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
0 |
0 |
5 |
0 |
4 |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
5 |
|
|
6 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
8 |
0 |
0 |
0 |
0 |
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
||||||||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
6 |
3 |
||||||||||||||
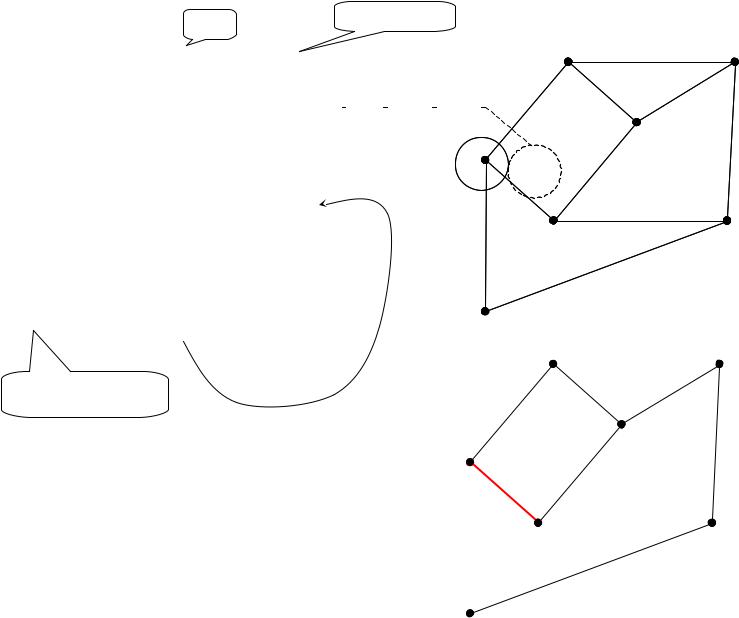
Удаляем столбец из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
||||
|
|
рассмотрения |
|
Добавляем вершину |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
5 к фрагменту и |
1 |
|
|
|
|
|
|
5 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
удаляем столбец |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
0 |
0 |
|
0 |
8 |
|||
|
|
|
0 |
6 |
1 |
|
0 |
0 |
|||
|
|
|
|
||||||||
|
|
6 |
0 |
4 |
|
5 |
0 |
||||
|
|
|
|
||||||||
|
|
|
1 |
4 |
0 |
|
0 |
0 |
|||
|
|
|
|
||||||||
|
|
|
0 |
0 |
(2) |
|
4 |
0 |
|||
|
|
|
0 |
5 |
0 |
|
0 |
3 |
|||
|
|
|
|
||||||||
|
|
|
0 |
0 |
0 |
|
3 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||
|
|
|
2 |
|
|
6 |
|
|
3 |
||
|
3 |
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||
1 |
|
|
|
|
|
2 |
|
5 |
|||
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
4 |
|
|
6 |
|
8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*
*
|
3 |
0 |
|
|
0 |
6 |
|
|
|
||
6 |
0 |
|
|
|
|
||
|
1 |
4 |
|
|
|
||
|
0 |
0 |
|
|
0 |
5 |
|
|
|
||
|
0 |
0 |
|
|
|
|
|
1 |
2 |
3 |
4 |
26
|
3 |
|
1 |
4 |
|
|
|
||
1 |
|
|
4 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
85
3
7
0 |
8 |
* |
|
|
|
|
|
0 |
0 |
|
|
|
|||
5 |
0 |
||
|
|||
0 |
0 |
|
|
* |
|||
4 |
0 |
* |
|
0 |
3 |
|
|
|
|||
3 |
0 |
|
|
5 6 |
7 |
|
|
|
1
3
 5 2 5 42
5 2 5 42
 6
6
|
3 |
|
0 |
|
|
0 |
8 |
|
* |
|
|
0 |
|
6 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||
6 |
|
0 |
|
|
5 |
0 |
|
|||
|
|
|
|
|
|
|||||
|
(1) |
|
4 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
* |
|||||
|
0 |
|
0 |
|
|
4 |
0 |
|
* |
|
|
0 |
|
5 |
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
0 |
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
2 |
|
|
6 |
|
|
3 |
||
3 |
|
|
1 |
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||
1 |
|
|
|
2 |
|
|
5 |
|||
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
4 |
|
|
6 |
|
8 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
8 |
* |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
0 |
0 |
* |
|
|
0 |
|
|
5 |
0 |
|
|
|
|
|
|
|||
|
|
4 |
|
|
0 |
0 |
|
|
|
|
|
* |
|||
|
|
0 |
|
|
4 |
0 |
* |
|
|
5 |
|
|
0 |
3 |
|
|
|
|
|
|
|||
|
|
0 |
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 |
6 |
|
3 |
|
1 |
|||
|
3 |
|
1 |
|
|
|
|
||
|
|
4 |
|
|
|
2 |
|||
|
|
|
|
|
|
5 |
|||
1 |
|
|
|
4 |
5 |
||||
|
2 |
|
2 |
|
2 |
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
6 |
1 |
|
||
8 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
8 |
* |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
0 |
0 |
* |
|
|
0 |
|
|
5 |
0 |
|
|
|
|
|
|
|||
|
|
(4) |
|
|
0 |
0 |
|
|
|
|
|
* |
|||
|
|
0 |
|
|
4 |
0 |
* |
|
|
5 |
|
|
0 |
3 |
|
|
|
|
|
|
|||
|
|
0 |
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 |
6 |
3 |
||||
|
3 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
1 |
|
2 |
|
2 |
5 |
||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
6 |
|
8 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|||
|
|
|
|
|
|
|
|
|
|
4 |
0 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
||
|
2 |
|
|
6 |
|
|
|
3 |
|
|
|
1 |
|||
|
3 |
|
1 |
|
4 |
4 |
|
|
|
|
|
|
5 |
2 |
|
1 |
|
|
|
2 |
|
|
|
5 |
|
|
2 |
|
|||
|
2 |
|
|
|
|
|
|
|
4 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5 |
|
|
|
4 |
|
|
|
6 |
2 |
1 |
4 |
|
|
8 |
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
* |
|
|
|
|
|
5 |
0 |
|
|
|
|
|
|
* |
||
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
* |
||
|
|
|
|
|
(4) |
0 |
* |
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 |
6 |
3 |
||||
|
3 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
1 |
|
2 |
|
2 |
5 |
||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
6 |
|
8 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6
|
2 |
6 |
3 |
|
||||
|
3 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|
1 |
|
2 |
|
2 |
5 |
|
||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
6 |
|
|
8 |
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 *
0 *
0 *
0 *
0 *
3 *
0
7
1
5 2
24
4 |
6 |
1 |
4 |
|
3 |
1
3
1
8
7
|
|
|
|
|
|
8 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
* |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
* |
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
* |
||
|
|
|
|
|
|
0 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) * |
||
|
|
|
|
|
|
0 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
|
||
|
||||||||
|
2 |
|
|
6 |
|
3 |
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
2 |
|
|
|
5 |
|||
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
4
5
 6
6
3
|
|
|
|
0 |
3 |
0 |
0 |
2 |
0 |
8 |
* |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
0 |
6 |
1 |
0 |
0 |
0 |
* |
||
|
|
|
|
0 |
6 |
0 |
4 |
0 |
5 |
0 |
|
||
|
|
|
|
* |
|||||||||
|
|
|
|
0 |
1 |
4 |
0 |
2 |
0 |
0 |
|
||
|
|
|
|
* |
|||||||||
|
|
|
|
2 |
0 |
0 |
2 |
0 |
4 |
0 |
* |
||
|
|
|
|
0 |
0 |
5 |
0 |
4 |
0 |
3 |
|
||
|
|
|
|
* |
|||||||||
|
|
|
|
8 |
0 |
0 |
0 |
0 |
3 |
0 |
* |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
U |
U |
U |
|
U |
U |
U |
|
||
|
2 |
|
|
6 |
|
|
3 |
|
|
1 |
|||
|
3 |
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|
|
2 |
|||
|
|
|
|
|
4 |
|
|
|
|
5 |
|||
1 |
|
|
|
|
|
|
5 |
|
|||||
|
2 |
|
|
2 |
|
|
|
|
2 |
4 |
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||
|
|
5 |
|
|
|
|
|
6 |
1 |
|
|
||
8 |
|
|
|
|
|
|
|
4 |
3 |
||||
|
|
|
|
|
|
|
|
|
|
2 |
3 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
|
|
|
|
|
||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
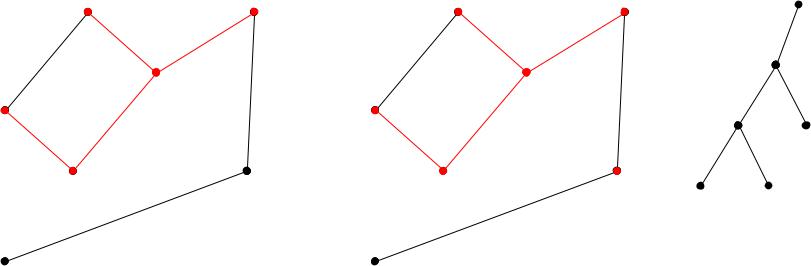
w=2+2+1+4+4+3=16 |
||||
|
|
|
|
|
|
|
|
|
|
||||
