
Электронные пучки
.pdf
Александров А.Ф., Кузелев М.В. Физика электронных пучков
r
P θ |
|
|
r(z) |
θ' |
P' |
|
А |
O |
В |
||||
|
|
ξ |
|
|
ξ' |
z |
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
Рис. 8.1
Ход лучей в собирающей линзе
31
Александров А.Ф., Кузелев М.В. Физика электронных пучков
точками “А” и “В” около точки z = 0 . Левее точки “А” показатель преломления равен n = n01 , правее точки “В” n = n02 , где n01,2 - постоянные. Ход луча, выходящего из точки “Р” и
приходящего в точку “Р'”, для случая собирающей линзы изображен на Рис. 8.1. Проинтегрируем уравнение (8.17) по z от точки “Р” до точки “Р'”. Имеем
n02 |
dr′ |
− n01 |
dr |
= ∫В r(z)n0′′(z)dz . |
(8.18) |
|
dz |
dz |
|||||
|
|
А |
|
Здесь dr dz и dr′
dz и dr′ dz - производные функции r(z) в точках “Р” и “Р'” соответственно.
dz - производные функции r(z) в точках “Р” и “Р'” соответственно.
Предположим теперь, что линза тонкая, т.е. размер области АВ мал по сравнению с расстояниями от точек “Р” и “Р'” до начала координат. Тогда (8.18) можно записать следующим образом:
n02 |
dr′ |
− n01 |
dr |
= r0 ∫В n0′′(z)dz , |
(8.19) |
|
dz |
dz |
|||||
|
|
А |
|
где r0 = r(0) . Вне линзы, поскольку среда однородная, лучи являются прямыми. Из рисунка видно, что (в параксиальном приближении)
|
dr |
= tgθ =θ = − |
r0 |
dr |
′ |
= −tgθ |
′ |
= −θ |
′ |
= − |
r0 |
(8.20) |
|||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||
|
dz |
ξ |
|
dz |
|
|
ξ′ |
||||||||||||||||||
(надо иметь в виду, что ξ < 0 ). Подставляя (8.20) в (8.19), получаем формулу линзы |
|
||||||||||||||||||||||||
|
f |
|
+ |
f ′ |
= −1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.21) |
||||
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ξ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где фокусные расстояния линзы |
f |
и |
f ′ |
определяются формулами |
|
||||||||||||||||||||
|
1 |
|
= − |
|
1 |
В n0′′(z)dz, |
|
1 |
|
|
= |
1 |
|
В n0′′(z)dz . |
|
|
(8.22) |
||||||||
|
f |
|
|
|
f ′ |
|
|
|
|
||||||||||||||||
|
|
|
n01 А∫ |
|
|
n02 А∫ |
|
|
|
|
|
|
|
|
|||||||||||
При f > 0 и |
f ′ < 0 линза является собирающей, в чем легко убедиться, анализируя формулу |
||||||||||||||||||||||||
(8.21). В следующем параграфе будет показано, что по формулам (8.22) могут быть рассчитаны и фокусные расстояния электростатической линзы, применяемой для фокусировки электронных пучков.
§9. Аналогия между движением электрона в электростатическом поле
ираспространением луча в прозрачной среде
Сучетом того, что заряд электрона отрицательный запишем уравнение движения нерелятивистского электрона в электростатическом поле с потенциалом ϕ(r) в виде
m |
dvr |
=| e | |
∂ϕr . |
(9.1) |
|
dt |
|||||
|
|
∂r |
|
Будем нормировать потенциал так, что он равен нулю там, где электрон имеет нулевую ско-
32

Александров А.Ф., Кузелев М.В. Физика электронных пучков
рость. Тогда для кинетической энергии электрона имеем
|
mv2 |
|
r |
|
|
|
=| e | ϕ(r ) . |
(9.2) |
|
2 |
||||
Из (9.2) для абсолютной величины скорости электрона находим следующее выражение: |
|
|||
|
|
2 | e | |
r |
|
v = |
m |
ϕ(r ) . |
(9.3) |
|
Из (9.3) следует, что электрон может находиться только в тех областях пространства, где
ϕ(rr) > 0 .
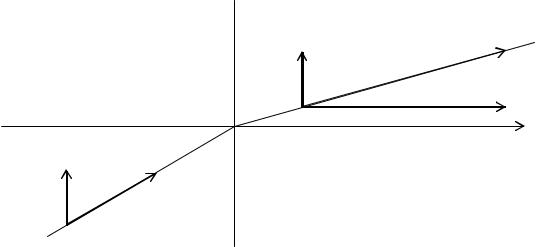
Предположим, что электрон из полупространства z < 0 , где потенциал ϕ(r) постоя-
нен и равен ϕ 1 , перелетает в полупространство z > 0 , где потенциал также постоянен и ра-
вен ϕ 2 . Рассмотрим, что происходит с траекторией электрона при переходе через границу раздела z = 0 (Рис. 9.1). Разложим скорость электрона на составляющие: v - составляющая нормальная к границе раздела и v|| - составляющая тангенциальная к границе раздела. По-
скольку ∂ϕ ∂x = ∂ϕ ∂y = 0 , то силы тангенциальные к границе раздела z = 0 отсутствуют.
Тогда из уравнения (9.1) следует сохранение тангенциальной составляющей скорости электрона
v|| 1 |
= v|| 2 . |
|
|
|
|
(9.4) |
||||||
Нормальная составляющая меняется, |
поскольку на границе z = 0 на электрон действует |
|||||||||||
мгновенная бесконечно большая сила |
|
|
||||||||||
| e | |
∂ϕ |
|
= (ϕ 2 −ϕ 1 )δ(z) . |
|
|
(9.5) |
||||||
∂z |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Изменение полной скорости v = v2 |
+ v2 |
можно вычислить по формуле (9.3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|| |
|
v |
= |
|
|
2 | e | ϕ |
1,2 |
. |
|
|
(9.6) |
|||
1,2 |
|
|
|
|
m |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку v|| 1 |
= v1 sinα , v|| 2 = v2 sin β , то из (9.4) имеем |
|||||||||||
|
sinα |
= |
v2 |
. |
|
|
|
|
(9.7) |
|||
|
|
|
|
|
|
|
||||||
|
sin β |
|
v |
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
И, наконец, подставляя (9.6) в (9.7), находим следующий закон преломления электронных траекторий на границе скачкообразного изменения электростатического потенциала:
sin α |
= |
ϕ 2 |
. |
(9.8) |
|
sin β |
ϕ 1 |
||||
|
|
|
Вспомним теперь закон преломления луча света в оптике при переходе луча из одно-
родной среды с постоянным показателем n1 в однородную среду с постоянным показателем
33
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ϕ = ϕ 1 |
|
ϕ = ϕ 2 |
|
v |
vr |
|
|| 1 |
2 |
|
|
v 2 |
|
β |
z |
|
α |
|
v |
vr |
|
|| 1 |
1 |
|
 v 1
v 1
z=0
Рис. 9.1
Преломление траектории электрона при переходе через скачок потенциала
34
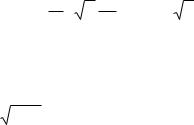
Александров А.Ф., Кузелев М.В. Физика электронных пучков
преломления n2 (закон Снеллиуса). Если α - угол падения луча на границу раздела сред, а
β - угол преломления, то имеет место соотношение
sinα |
= |
n2 |
. |
(9.9) |
sin β |
|
|||
|
n |
|
||
|
1 |
|
|
|
Сравнивая формулы (9.8) и (9.9), замечаем аналогию между движением электрона в электростатическом поле с потенциалом ϕ(r) и распространением светового луча в среде с показа-
телем преломления n(rr) . Роль коэффициента преломления в электростатике играет корень квадратный из электростатического потенциала. Правда доказано это пока только для резких границ раздела потенциалов и сред.
Перейдем к рассмотрению общего случая плавного изменения электростатического потенциала. В статическом поле траектория частицы стационарна в том смысле, что все частицы, вылетающие из одной точки с одной и той же скоростью, движутся по одинаковым траекториям. Если известен закон движения частицы r = r(t) , то уравнение траектории по-
лучается переходом от времени t к натуральному параметру l - расстоянию вдоль траекто-
рии от ее начальной точки. Из уравнения drr dt = vr , взятого по модулю, следует связь между дифференциалами
dt = vr , взятого по модулю, следует связь между дифференциалами
dt = |
1 |
dl . |
(9.10) |
|
|||
|
v |
|
|
Заметим, что если имеет место соотношение (9.3), то v > 0 и каких-либо ограничений на использование соотношения (9.10) нет. Переходя при помощи (9.10) в уравнении (9.1) от переменной t к переменной l , преобразуем это уравнение к виду
|
|
d |
|
|
drr |
|
|
|
mv |
|
|
v |
|
|
=| e | grad ϕ . |
(9.11) |
|
|
|
dl |
||||||
|
dl |
|
|
|
||||
Подставляя в (9.11) скорость v |
из (9.3), получим следующее дифференциальное уравнение |
|||||||
для траектории электрона rr(l) в электростатическом поле: |
||||||||
d |
|
ϕ |
drr |
= grad ϕ . |
(9.12) |
|||
|
|
|
|
|||||
dl |
|
|
dl |
|
|
|||
Сравнивая последнее уравнение с уравнением (8.14), видим их полную идентичность. При этом роль показателя преломления n(r) в оптике, в электростатике играет функция
ϕ(rr) . Уравнение (9.12) является основным уравнением электронной оптики. Заметим, что оптика электронов в электростатическом поле открывает принципиально новые возможности в сравнении с обычной оптикой световых лучей. В обычной оптике показатель преломления прозрачных сред изменяется в пределах нескольких единиц (у стекла n ≈1.5 , а у алмаза n ≈ 2.5 ). Кроме того, показатель преломления можно изменить, только заменив среду. В
35
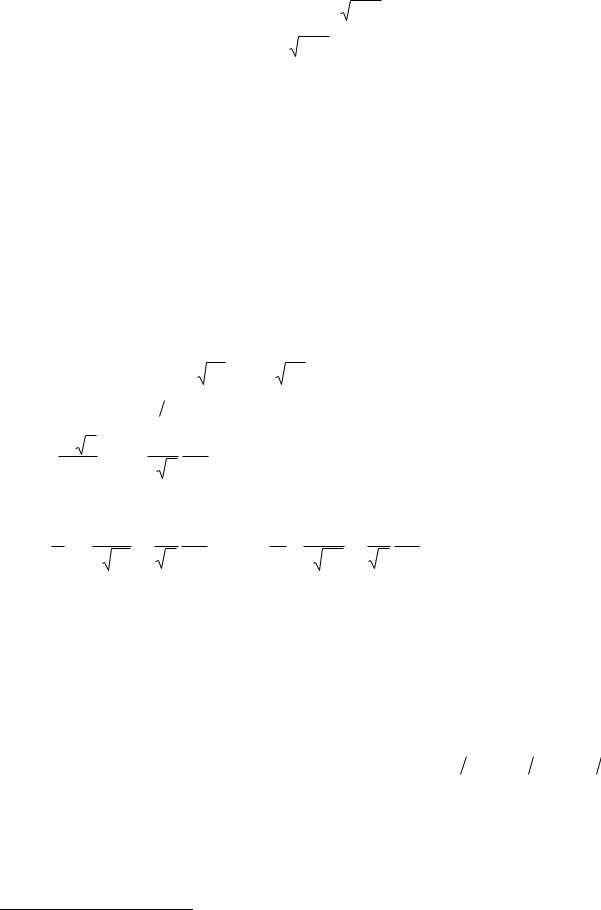
Александров А.Ф., Кузелев М.В. Физика электронных пучков
электронной оптике “показатель преломления” ϕ(rr) определяется потенциалом электро-
дов, создающих поле. Поэтому величина ϕ(rr) может меняться в самых широких пределах,
причем в одном и том же устройстве.
Используем уравнение (9.12), точнее его аналогию с уравнением (8.14), для расчета фокусного расстояния тонкой центрированной электростатической линзы. Такую линзу можно осуществить с помощью двух соосных полых металлических цилиндров: левый ци-
линдр с потенциалом ϕ 1 расположен в области левее точки “А” (см. Рис. 8.1), правый ци-
линдр с потенциалом ϕ 2 расположен правее точки “В”. В области между точками “А” и “В”
имеется неоднородное электростатическое поле, обладающее фокусирующим воздействием на электроны. Траектория электрона вполне аналогична лучу света, изображенному на Рис. 8.1.
Принимая во внимание аналогию с геометрической оптикой, воспользуемся форму-
лами (8.22), в которых n01 = |
|
ϕ 1 |
, n02 |
= ϕ 2 |
. Учтем также, что оси симметрии системы име- |
|||||||||||||
ет место равенство (∂ϕ ∂r)r=0 |
= 0 , поэтому |
|
|
|
|
|
|
|
||||||||||
|
2 |
ϕ |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
= |
∂ ϕ |
. |
|
|
|
|
|
|
|
|
|
||||
|
∂r |
2 |
|
|
ϕ |
∂r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
r=0 |
2 |
|
r=0 |
|
|
|
|
|
|
|
|
|
||||
Тогда из формул (8.22) имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
1 |
+∞ |
1 |
∂2ϕ |
|
|
1 |
|
1 |
+∞ |
1 ∂2ϕ |
|
|
|||
|
= − |
|
|
|
|
2 |
|
dz, |
|
= |
|
|
|
2 |
|
dz . |
(9.13) |
|
f |
|
∫ |
ϕ |
∂r |
|
f ′ |
|
∫ |
ϕ ∂r |
|
||||||||
|
2 ϕ |
1 -∞ |
|
r=0 |
|
2 ϕ 2 -∞ |
|
r=0 |
|
|
||||||||
Пределы интегрирования в (9.13) взяты бесконечными, поскольку потенциал изменяется (в отличие от обычной оптики) и вне области между точками “А” и “В”. Преобразуем формулы (9.13) к более удобному виду. Электростатический потенциал ϕ удовлетворяет уравнению Лапласа
∂2ϕ |
+ |
∂2ϕ + |
∂2ϕ |
= 0 . |
(9.14) |
||||||
∂z2 |
|
|
∂x2 |
∂y2 |
|
|
|
|
|||
Из-за осевой симметрии системы на оси выполнены равенства ∂2ϕ ∂x2 |
= ∂2ϕ ∂y2 = ∂2ϕ ∂r2 (*). |
||||||||||
Поэтому из (9.14) следует, что |
|
||||||||||
|
2 |
|
|
|
1 |
|
2 |
|
|
|
|
|
∂ ϕ |
|
= − |
∂ ϕ |
|
(9.15) |
|||||
|
2 |
|
|
||||||||
|
∂r |
|
2 |
|
∂z |
2 |
. |
||||
|
|
r=0 |
|
|
r=0 |
|
|||||
Подставляя (9.15) в (9.14) для фокусных расстояний тонкой электронной линзы получаем
(*) Поскольку исходное уравнение (9.1) записано в декартовых координатах, то r не является цилиндрической координатой (!), а только обозначает любую из декартовых координат поперечных к оси z . Т.е. r имеет знак: r > 0 - выше оптической оси, r < 0 - ниже. При смене знака у r(z) изображение перевертывается.
36

Александров А.Ф., Кузелев М.В. Физика электронных пучков
следующие выражения:
1 |
|
1 |
+∞ |
1 ∂2ϕ |
|
1 |
|
1 |
+∞ |
1 ∂2ϕ |
|
|
||||
|
= |
|
|
|
2 |
|
dz, |
|
= − |
|
|
|
2 |
|
dz . |
(9.16) |
f |
|
∫ |
ϕ ∂z |
|
f ′ |
|
∫ |
ϕ ∂z |
|
|||||||
4 |
ϕ 1 -∞ |
|
r=0 |
|
|
4 ϕ 2 -∞ |
|
r=0 |
|
|
||||||
Если при |
x → ±∞ выполнены условия (∂ϕ ∂x)r=0 |
= 0 |
(это имеет место в случае линзы, со- |
|||||||||||||
стоящей из двух соосных полых металлических цилиндров), то в (9.16) целесообразно выполнить интегрирование по частям, что дает
1 |
|
1 |
+∞ |
|
|
∂ϕ |
2 |
|
|
1 |
|
1 |
+∞ |
|
|
∂ϕ |
2 |
|
|
|
= |
|
−3 2 |
|
|
dz, |
= − |
|
−3 2 |
|
|
dz . |
(9.17) |
||||||||
f |
|
∫ ϕ |
|
|
|
|
|
f ′ |
|
∫ ϕ |
|
|
|
|
|
|||||
|
8 ϕ 1 -∞ |
|
|
∂z |
|
r=0 |
|
|
8 ϕ 2 -∞ |
|
|
∂z |
|
r=0 |
|
|
||||
Поскольку |
f > 0 |
и |
f ′ < 0 , то тонкая электростатическая линза является собирающей. В |
|||||||||||||||||
обычной оптике тонкие линзы могут быть как собирающими, так и рассеивающими. Используя набор тонких электростатических линз (толстая линза) можно получить и эффект рассеяния электронов.
§ 10. Строгая теория параксиальных аксиально-симметричных электронно-оптических систем
Помимо фокусных расстояний электронно-оптическая система характеризуется коэффициентами линейного и углового увеличения, а также рядом соотношений общего характера. Все это может быть получено на основании аналогии с геометрической оптикой световых лучей. Мы же проведем соответствующее рассмотрение, основываясь на электроннооптическом уравнении (9.12).
Запишем уравнение (9.12) для центрированной электронно-оптической системы в параксиальном приближении. В этом приближении можно записать
∂ |
|
∂ |
|
|
1 |
|
2 |
∂ ϕ0 (z) |
∂ |
|
|
r |
2 |
|
|
|
|
|
|
|
|||||||||
|
ϕ(r, z) = |
|
ϕ0 |
(z) + |
|
r |
|
2 |
2 = |
|
|
ϕ0 1+ |
|
|
∂r |
∂r |
2 |
|
∂r |
|
|
4ϕ0 |
|||||||
|
|
|
|
|
|
∂r |
|
|||||||
∂2ϕ0
∂r2
|
|
|
r |
′′ |
(z) |
|
|
|
|
= − |
ϕ0 |
. |
(10.1) |
||
|
4 |
ϕ0 (z) |
|||||
|
|
|
|
||||
Здесь ϕ0 (z) = ϕ(0, z), ϕ0′′(z) = ∂2ϕ0 (z) ∂z2 . При получении (10.1) было использовано соотно-
∂z2 . При получении (10.1) было использовано соотно-
шение (9.15). При dl = dz z - компонента уравнения (9.12) удовлетворяется тождественно, а r-компонента преобразуется к следующему виду:
|
d |
ϕ0 (z) |
dr(z) |
= − |
r(z) ϕ0′′(z) |
, |
(10.2а) |
|||||||
|
dz |
|
dz |
|
4 ϕ0 (z) |
|||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d 2r |
|
+ |
ϕ0′ |
|
dr |
+ |
ϕ0′′ |
|
r = 0 . |
|
(10.2б) |
||
|
dz2 |
2ϕ0 |
|
dz |
|
|
|
|||||||
|
|
|
|
4ϕ0 |
|
|
|
|||||||
Уравнение (10.2) и есть искомое уравнение центрированной электронно-оптической системы
37
Александров А.Ф., Кузелев М.В. Физика электронных пучков
в параксиальном приближении.
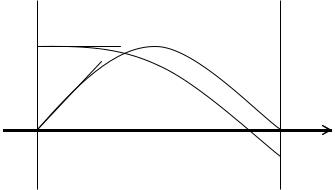
Построим общее решение уравнения (10.2) в области a < z < b . Пусть r1,2 (z) - линейно независимые решения уравнения (10.2), удовлетворяющие следующим начальным условиям в начальной точке траектории электрона:
r1 (a) = 0, |
r2 |
(a) =1, |
(10.3) |
|
′ |
′ |
(a) = 0. |
||
r1 (a) =1, |
r2 |
|
||
Общее решение уравнения (10.2) дается линейной комбинацией линейно независимых решений r1,2 (z)
r(z) = c1r1 (z) + c2r2 (z) . |
(10.4) |
В силу условий (10.3) постоянные c1,2 |
в решении (10.4) имеют простой физический |
смысл. Поскольку r(a) = c2 , то c2 задает расстояние электронной траектории от главной оп-
тической оси в плоскости z = a . Далее, т.к. r′(a) = c1 , то c1 определяет тангенс угла наклона траектории электрона к оптической оси системы в той же плоскости. Предположим теперь,
что r1 (b) = 0 (Рис. 10.1). Тогда, как следует из (10.4), справедливо соотношение |
|
r(b) = c2r2 (b) , |
(10.5) |
имеющее наглядный физический смысл: все траектории, вышедшие в плоскости |
z = a из |
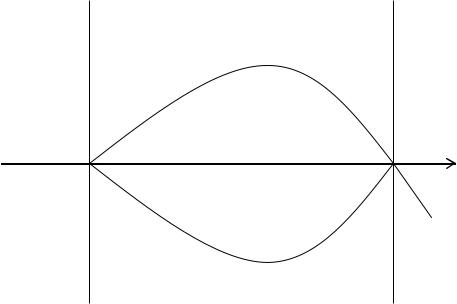
точки r = c2 , в плоскости z = b соберутся в точке r = c2r2 (b) . Если c2 = 0 , то r(a) = r(b) = 0 . Следовательно, пучок траекторий вышедших в плоскости z = a из точки на главной оптической оси, в плоскости z = b соберется в точке лежащей на той же главной оси. Это означает фокусировку пучка (Рис. 10.2). Заметим, что мы имеем право говорить именно о пучке тра-
екторий, т.е. о пучке электронов, поскольку результат (10.5) не зависит от постоянной c1 , за-
дающей угол α = arctanc1 вылета электрона из точки r = 0 в плоскости z = a . Угол β , под которым траектории пересекают оптическую ось в плоскости z = b , равен α = arctan c1r1′(b) .
Как и в обычной оптике, плоскость z = a называют плоскостью объекта, а плоскость z = b - плоскостью изображения (Рис. 10.2).
Таким образом, аксиально-симметричные электростатические поля пригодны для получения точечных изображений при помощи параксиальных электронных пучков. В плоскости объекта и в плоскости изображения имеют место соотношения
r(a) = c2 , |
r(b) = c2r2 (b) . |
(10.6) |
|||
Величина |
|
|
|
|
|
K |
l |
= |
r(b) |
= r (b) |
(10.7) |
|
|||||
|
|
r(a) |
2 |
|
|
|
|
|
|
|
|
38
Александров А.Ф., Кузелев М.В. Физика электронных пучков
дает изменение (увеличение или уменьшение) линейных размеров объекта при его
r1 (z)
r2 (z)
z
z = a |
z = b |
Рис. 10.1
Траектории электрона, описываемые решениями r1,2 (z)
39
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Плоскость |
Плоскость |
объекта |
изображения |
α |
β |
z |
β
z = a z = b
Рис. 10.2
Получение изображения точечного объекта, расположенного на главной оптической оси. α = arctanc1, β = arctanc1r1′(b)
40
