Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
Здесь введены обозначения |
|
|
|
∆ |
α |
(r) = ω − k V (s) (r) −lω(s) (r), |
|
|
|
|
|
|
|
|
z |
αz |
α |
|
|
|
Ω |
2α |
(r) = s |
Ω |
α |
γ |
−1 |
+ 2ω(s) (r), |
|
|
|
|
|
|
α |
|
α |
α |
|
|
|
Ω1α (r) = sα Ωαγα−1 |
+ωα(s) (r) + |
d |
rωα(s) (r), |
(40.12) |
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωα(s) |
(r) = |
Vαϕ(s) (r) |
, |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а sα и Ωα |
определены в (22.6). Очевидно, что величины ωα(s) (r) |
являются введенными в |
(22.4) угловыми скоростями вращения частиц сорта α .
Из системы (40.11) легко находим выражения для амплитуд возмущений скоростей
v |
(r) = −i |
eα |
|
|
γ −1D−2 (r) ∆ |
α |
|
(r) |
dψ |
|
− Ω |
2α |
(r) |
l |
ψ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αr |
|
|
mα |
|
|
α |
α |
|
|
|
|
|
|
dr |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
(r) = − |
|
eα |
γ −1D−2 |
(r) Ω |
|
|
(r) |
dψ |
− ∆ |
α |
(r) |
l |
ψ |
, |
|
|
|
|
|
|
|
(40.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αϕ |
|
mα |
|
|
α |
α |
|
1α |
|
|
|
dr |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vαz |
(r) = kz |
e |
|
|
γα−3∆−α1 (r)ψ − |
e |
γα−1Dα−2 (r)∆−α1 (r) |
dV (s) |
(r) |
dψ |
|
l |
|
|
α |
|
|
|
α |
|
αz |
|
∆α (r) |
|
− Ω2α (r) |
|
ψ |
, |
mα |
|
|
mα |
|
dr |
|
dr |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D2 |
(r) = ∆2 |
(r) − Ω |
(r)Ω |
2α |
(r) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(40.14) |
α |
α |
|
|
|
1α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка выражений (40.10) и (40.13) в первое уравнение системы (40.7) приводит к следующему выражению для амплитуды возмущения плотности частиц сорта α :
|
1 d |
|
dψ |
|
l2 |
|
4πeα nα (r) = |
|
|
|
rε α |
|
|
+ |
|
ε αψ + |
|
|
|
dr |
r2 |
|
r dr |
|
|
|
|
l |
|
1 d |
|
l |
|
|
|
(s) |
+ |
ψ |
(Ω2αε α )+ kz |
ψΩ2α |
ε α dVαz |
r |
∆α |
|
dr |
r |
2 |
|
dr |
|
|
|
|
|
∆α |
|
Здесь
ε α (r) = |
ωL2α (r) |
, ε||α (r) = |
ωL2α (r) |
- |
(40.16) |
2 |
(r) |
3 |
2 |
|
γα (r)Dα |
|
γα |
(r)∆α (r) |
|
|
вклады частиц сорта α в поперечную и продольную диэлектрические проницаемости соот-
ветственно, а |
|
|
|
|
ωL2α (r) = |
4πeα2 Nα(s) (r) |
- |
|
|
|
(40.17) |
|
|
|
|
|
mα |
|
|
|
|
квадраты ленгмюровских частот частиц соответствующего сорта. |
Наконец, подставляя величины |
~ |
и |
~ |
из (40.10) и выражения (40.15) в уравнение |
ϕ |
Nα |
Пуассона (40.5), получим следующее основное уравнение линейной теории электростатических колебаний цилиндрического столба радиально неоднородной заряженной плазмы

|
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|
1 d |
|
|
dψ |
|
l2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
r 1 |
− ∑ε α |
|
|
− |
|
|
1 |
− ∑ε α ψ − kz |
1 − ∑ε||α ψ |
= |
|
|
|
|
r dr |
dr |
r |
2 |
|
|
|
|
|
α |
|
|
|
|
|
α |
|
|
|
|
|
α |
|
|
|
|
|
(40.18) |
|
|
|
|
|
|
l |
|
|
|
|
d |
|
|
|
|
|
l |
|
|
|
|
(s) |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε α dVαz |
|
|
|
|
|
|
|
= − |
|
ψ ∑ ∆α |
|
(Ω2αε α ) |
− kz |
|
ψ ∑ Ω2α |
2 |
|
|
. |
|
|
|
|
|
|
r |
dr |
r |
dr |
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
α |
|
∆α |
|
|
|
Заметим, что при получении выражения (40.15) и уравнения (40.18) было использовано соотношение
|
Ω2α − Ω1α = −r |
dωα(s) |
= |
r |
|
d |
(∆α + kzVα(zs) ), |
(40.19) |
|
dr |
l dr |
|
|
|
|
|
которое является следствием формул (40.12).
§ 41. Электрон – электронные двухпотоковые неустойчивости
Предположим, что плотности электронов пучка, электронов и ионов плазмы равномерно распределены по поперечному сечению круглого волновода радиуса R , а продольная скорость пучка постоянна, т.е. Vbz(s) (r) = u = const . Пусть также статический заряд в системе нейтрализован полностью, однородное внешнее продольное магнитное поле достаточно сильное, поэтому дрейфовым вращением компонент плазмы можно пренебречь, т.е. поло-
жить ωα(s) = 0 . Кроме того, пренебрежем движением тяжелых ионов. При этом дифференци-
альное уравнение (40.18) записывается в виде
|
|
|
|
|
|
|
d |
|
|
|
l |
2 |
|
|
|
2 |
|
|
|
|
|
1 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
r |
|
|
|
|
− |
|
|
|
ψ − kz |
ε||ψ = 0 . |
(41.1) |
|
|
|
|
|
dr |
|
|
r |
2 |
|
|
|
r dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь ε и ε|| |
- полные поперечная и продольная диэлектрические проницаемости, опреде- |
ляемые выражениями |
|
|
|
|
|
|
|
|
|
ε =1− |
|
|
|
|
ω |
2 |
|
|
− |
|
|
ω2 |
γ −1 |
, |
|
|
|
|
Le |
|
|
|
Lb |
0 |
|
|
|
|
|
|
|
ω2 − Ωe2 |
|
|
|
(ω − kzu)2 − Ωe2 γ02 |
(41.2) |
|
|
|
|
|
|
ω |
2 |
|
|
|
ω |
2 |
γ −3 |
|
|
|
ε |
|
=1 − |
|
|
|
, |
|
|
|
|| |
|
|
Le − |
|
|
|
Lb |
0 |
|
|
|
|
|
|
|
|
|
ω2 |
|
|
(ω − kzu)2 |
|
|
|
|
где γ0 = (1 −u2 c2 )−1 2 - невозмущенный релятивистский фактор электронов пучка. Уравнение
(41.1) дополняется следующим граничным условием на металлической стенке волновода:
ψ (R) = 0 .
Решение уравнения (41.1), ограниченное в нуле и удовлетворяющее указанному гра-
ничному условию, выражается через функцию Бесселя порядка l : ψ (r) = const Jl (k r) , где k = µls 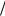 R , а µls - корень функции Бесселя. Подставляя приведенное решение в уравнение
R , а µls - корень функции Бесселя. Подставляя приведенное решение в уравнение
(41.1), получим следующее условие его разрешимости – дисперсионное уравнение:
Александров А.Ф., Кузелев М.В. Физика электронных пучков
k 2ε + kz2ε|| = 0 . |
(41.3) |
В отсутствии электронного пучка, |
т.е. при ωLb = 0 , дисперсионное уравнение (41.3) |
определяет две ветви объемных потенциальных плазменных волн магнитоактивной плазмы.
|
В длинноволновой области, при kz2 |
<< k 2 |
частоты этих волн определяются соотношениями |
|
ω2 = |
k 2 |
|
ω2 |
Ω2 |
|
, |
ω2 = ω2 |
+ Ω2 |
− |
k 2 |
|
ω2 |
Ω2 |
. |
(41.4) |
|
z |
|
Le |
e |
|
z |
|
Le |
e |
|
k 2 |
ωLe2 + Ωe2 |
k 2 |
ωLe2 + Ωe2 |
|
|
|
|
Le |
e |
|
|
|
|
|
В противоположном |
коротковолновом |
пределе, |
при |
kz2 >> k 2 , решения дисперсионного |
|
уравнения (41.3) даются формулами (ωLe |
≠ Ωe ): |
|
|
|
|
ω2 = ω2 |
+ |
k 2 |
|
ω2 |
Ω2 |
, |
ω2 = Ω2 |
+ |
k 2 |
|
ω2 |
Ω2 |
. |
(41.5) |
|
|
|
Le |
e |
|
|
Le |
e |
|
kz2 |
ωLe2 − Ωe2 |
k 2 |
Ωe2 −ωLe2 |
|
Le |
|
|
|
e |
|
|
|
|
Дисперсионные кривые для волн (41.4), (41.5) (их иногда называют “косыми” ленгмюров-
скими волнами) – линии “a” и “b” - для случая Ωe > ωLe представлены на Рис. 41.1.
Наиболее важные пучковые неустойчивости, описываемые дисперсионным уравнением (41.3), обусловлены взаимодействием электронов пучка с волнами (41.4), (41.5) в условиях черенковского и циклотронного резонансов
|
ω = kzu, |
(41.6) |
|
ω = kzu,−Ωe γ0 , (ω > 0) . |
|
|
Резонансные точки на Рис. 41.1, на котором проведены также и прямые (41.6), отмечены цифрами 1, 2 – черенковские резонансы и 3, 4 – циклотронные резонансы. Заметим, что у точки 5, где условие циклотронного резонанса имеет вид
ω = kzu,+Ωe γ0 , (ω > 0) , |
(41.7) |
неустойчивости нет. Дело в том, что в области ω > 0 |
(ω < 0 ) резонансные условия |
ω = kzu m Ω0 (ω = kzu ± Ω0 ), где Ω0 > 0 некоторая частота осцилляций электрона, характери-
зуют разные физические механизмы взаимодействия электрона с волной, а именно: аномальный и нормальный эффекты Доплера. Неустойчивость прямолинейного электронного пучка возможна только в условиях аномального эффекта Доплера (а также конечно и в условиях эффекта Черенкова).
Характерные дисперсионные кривые уравнения (41.3) с учетом и плазмы и электрон-
ного пучка представлены на Рис. 41.2. Над зонами волновых чисел kz , где имеются неустой-
чивости, расположены “раздвижки” дисперсионных кривых. Эти зоны отмечены на рисунке стрелками.
В общем случае решение уравнения (41.3) затруднительно. Поэтому найдем комплексные частоты ω только при резонансных неустойчивостях электронного пучка малой
203
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
14 |
ω |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
10 |
|
|
|
|
|
8 |
5 |
2 |
|
4 |
"b" |
6 |
|
|
|
|
|
|
|
4 |
|
|
|
3 |
"a" |
|
1 |
|
|
2 |
|
|
|
k z |
0 |
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
Рис. 41.1
Дисперсионные кривые электростатических волн в магнитоактивной плазме и точки черенковского – 1 и 2 – и циклотронного – 3 и 4 - резонансов
ω
14
12
10
8
6 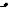
4
2
k z
0
Рис. 41.2
Характерные дисперсионные кривые уравнения (41.3)
Александров А.Ф., Кузелев М.В. Физика электронных пучков
плотности. Запишем дисперсионное уравнение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
γ −3 |
|
|
|
|
|
|
|
|
2 |
|
|
ω |
2 |
|
|
2 |
|
ω |
2 |
|
kz2 |
Lb |
0 |
|
2 |
|
|
|
D |
(ω, k |
|
− |
|
+ k |
− |
|
|
(ω − k |
u) |
|
|
. |
(41.8) |
|
) ≡ k |
1 |
|
Le |
|
1 |
|
Le |
= |
|
z |
|
|
|
|
0 |
|
z |
|
|
|
ω2 − Ω2 |
|
|
z |
|
ω2 |
|
2 |
|
ωLb2 γ0−1 |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
k |
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ω − kzu) − Ωe γ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первой формой записи дисперсионного уравнения (41.8) будем пользоваться при рассмотрении черенковских неустойчивостей, а второй – при рассмотрении неустойчивостей в услови-
ях циклотронного резонанса. Функция D0 (ω, kz ) определяет спектры частот объемных плаз-
менных волн.
Для вычисления инкрементов черенковских неустойчивостей представим частоту ω в виде (см. § 39)
ω = ω1,2 |
+δω1,2 |
= kz1,2u +δω1,2 , |
| δω1,2 | << ω1,2 , |
(41.9) |
где ω1,2 и kz1,2 - решения следующей системы уравнений |
|
D0 (ω, kz ) = 0, |
ω − kzu = 0 , |
|
|
|
|
|
|
|
|
(41.10) |
т.е. ω1,2 и kz1,2 |
являются координатами точек 1 и 2 на Рис. 41.1. Подставляя (41.9) в (41.8) и |
разлагая функцию D0 (ω, kz ) |
с точностью до линейных по δω1,2 |
членов, получим следующие |
выражения для инкрементов резонансных черенковских неустойчивостей: |
δω |
|
= |
−1+ i |
3 |
|
|
2 |
|
∂D01,2 −1 |
ω |
2 |
γ |
|
−3 |
1 3 |
(41.11) |
1,2 |
|
|
k |
z1,2 |
|
|
|
Lb |
0 |
. |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D0 |
|
2 |
2 |
|
2 |
|
2 |
−2 |
2 −4 |
] |
|
|
|
∂ω |
= 2ωωLe [k (ω |
|
|
− Ωe ) |
|
+ kz |
ω |
|
|
|
|
(41.12) |
величина в области ω > 0 положительная. Поэтому знаки в (41.11) проставлены верно, т.е. полученные инкременты соответствуют инкременту (39.10) неустойчивости, обусловленной одночастичным вынужденным эффектом Черенкова. Условие применимости выражений (41.11) следует из неравенства, приведенного в (41.9), и имеет вид
ωLb2 γ0−3 |
<< 2 1 + |
k 2u2ω2 |
|
. |
(41.13) |
|
2 |
2 |
|
(ω |
2 |
2 |
|
|
ωLe |
|
|
− Ωe ) |
|
|
|
Последнее является аналогом (39.11).
Для вычисления инкрементов циклотронных неустойчивостей представим частоту ω
в виде
ω = ω 3,4 +δω 3,4 = kz3,4u − Ωe γ0 +δω 3,4 , |
| δω 3,4 | << ω 3,4 , Ωe γ0 , |
(41.14) |
где ω 3,4 и kz3,4 - решения следующей системы |
уравнений |
|

Александров А.Ф., Кузелев М.В. Физика электронных пучков
D0 (ω, kz ) = 0, ω − kzu + Ωe γ0 = 0 , |
(41.15) |
т.е. ω 3,4 и kz3,4 являются координатами точек 3 и 4 на Рис. 41.1. Подставляя (41.14) в (41.8),
функцию D0 (ω, kz ) опять разложим с точностью до линейных по δω 3,4 |
членов. Кроме того, |
учитывая второе неравенство в (41.14), с той же точностью записываем |
|
(ω − kzu)2 − Ωe2 γ02 = −2(Ωe γ0 )δω 3,4 . |
(41.16) |
В результате из уравнения (41.8) находим следующие выражения для инкрементов резонансных циклотронных неустойчивостей в условиях аномального эффекта Доплера:
δω |
|
|
|
|
∂D |
−1 |
ω2 |
γ −2 1 2 |
(41.17) |
3,4 |
= i k 2 |
|
03,4 |
|
Lb |
0 |
. |
|
|
|
|
∂ω |
|
2Ωe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если сопоставить представления (41.14) и (39.6), а затем сравнить инкременты (41.17) и (39.14), то окажется, что структуры инкрементов полностью идентичны. Последнее не случайно: между коллективным эффектом Черенкова и аномальным эффектом Доплера имеется достаточно глубокая физическая аналогия.
§ 42. Электрон – ионные двухпотоковые неустойчивости
Неустойчивость, которая будет сейчас рассмотрена обусловлена относительным движением электронов пучка и ионов нейтрализующего фона. Но в отличие от обычной бунемановской неустойчивости плазмы с током (см. § 38) для ее развития требуется наличие свободной границы плазмы. Пусть электроны пучка и однозарядные ионы с постоянными плот-
ностями занимают однородную цилиндрическую область 0 ≤ r ≤ rb < R , где R - радиус ме-
таллического кожуха. Предположим, что продольная скорость электронов пучка V (s) (r) = u |
|
bz |
|
не зависит от r. Используя коэффициент зарядовой нейтрализации f |
<1, запишем следую- |
щую связь между квадратами ленгмюровских частот ионов фона |
и электронов |
пучка: |
ωLi2 = f (m M )ωLb2 . Поскольку масса иона M существенно больше массы электрона |
m , то |
ионы считаем не замагниченными, а электроны пучка наоборот полагаем сильно замагниченными внешним однородным продольным магнитным полем, что позволяет записать
|
|
|
|
|
|
|
ω2 |
|
|
|
|
ω2 |
|
|
|
|
|
ω2 |
|
|
ω2 |
γ −3 |
|
|
|
|
ε |
i |
= ε |
||i |
= |
Li |
, |
ε |
b |
= −γ |
Lb |
≈1 , Ω |
2b |
ε |
b |
≈ |
Lb , ε |
||b |
= |
Lb |
0 |
, |
(42.1) |
|
|
(ω − kzu −lωb(s) )2 |
|
|
|
|
|
ω2 |
|
|
|
0 Ωe2 |
|
|
|
Ωe |
|
|
|
где γ |
0 |
= (1−u2 |
c2 )−1 2 |
. Формулы (42.1) справедливы при |
r ≤ r ; вне указанной области вели- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
чины (42.1) равны нулю. Кроме того, при написании (42.1) предполагалось, что выполнены неравенства

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ω − kzu − lωb(s) 2 << Ωe2 γb2 , ωLb2 << Ωe2γ0−1, | ωb(s) | << Ωe γ0 , ωLi2 << ω2 , Ωi2 << ω2 . (42.2)
Подставляя (42.1) в (40.18), получим следующее дифференциальное уравнение для потенциала возмущений в электронно-ионной системе
1 d |
|
|
|
2 |
|
dψ |
|
l |
2 |
|
|
|
2 |
|
2 |
|
|
|
2 |
|
2 −3 |
|
l |
|
2 |
|
|
− |
ωLi |
− |
|
|
− |
ωLi |
|
− |
ωLi |
− |
ωLbγ0 |
|
ψ |
ωLb |
δ(r − rb ) . (42.3) |
|
|
|
|
|
2 |
|
|
|
r dr |
r 1 |
ω |
2 |
|
dr |
r |
1 |
ω |
2 |
ψ − kz |
1 |
ω |
2 |
2 |
ψ = |
r |
Ωe∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
Здесь ∆ = ω − kzu − lωb(s) . При записи правой части уравнения (42.3) учтено, что для ступен-
чатой функции ωLb2 (r) имеет место соотношение
dω2 |
(r) |
= −ω2 |
δ(r − r ) . |
(42.4) |
Lb |
|
|
|
dr |
|
Lb |
b |
|
|
|
|
|
Считаем также, что угловая скорость вращения электронного пучка ωb(s) совпадает с ωb(−) из
(23.12), т.е. не зависит от координаты r. Уравнение (42.3) дополняется граничным условием
ψ(R) = 0 .
Вслучае rb = R - полное заполнение волновода однородной плазмой – правая часть
уравнения (42.3) обращается в ноль, а его коэффициенты становятся постоянными. При этом из дифференциального уравнения (42.3) сразу следует дисперсионное уравнение
µ |
2 |
2 |
|
|
ω |
2 |
|
ω2 |
γ −3 |
|
|
|
|
|
ls |
|
|
Li |
|
Lb |
0 |
|
|
|
|
|
|
2 |
+ kz |
1 |
− |
|
2 |
− |
|
|
|
|
|
= 0 , |
(42.5) |
R |
ω |
|
(s) |
) |
2 |
|
|
|
|
|
|
(ω − kzu −lωb |
|
|
|
|
где µls - корень функции Бесселя. Хотя последнее уравнение и отличается от дисперсионного уравнения (38.2), оно фактически описывает обыкновенную бунемановскую неустойчивость плазмы с током, подробно исследованную нами в § 38. Поэтому рассматривать здесь особенностей, связанных с уравнением (42.5), мы не будем, а сразу перейдем к новой для нас неустойчивости, обусловленной относительным вращательным движением электронов пучка и ионов плазмы при наличии у них свободной границы.
Новое очевидно связано с правой частью уравнения (42.3), существенной только в случае rb < R , на чем и сосредоточимся. Более того, чтобы исключить влияние обыкновен-
ной бунемановской неустойчивости положим в уравнении (42.3) kz = 0 , записав его в виде
|
1 d |
|
|
|
2 |
|
|
|
|
l |
2 |
|
|
|
2 |
|
l |
|
2 |
|
|
|
|
r |
|
ωLi dψ |
|
|
|
|
ωLi |
|
ωLb |
|
δ(r − rb ) . |
(42.6) |
|
|
|
|
1 − |
|
2 |
|
|
|
− |
|
|
1 |
− |
|
2 |
ψ = |
|
ψ |
|
|
|
r dr |
ω |
|
dr |
r |
2 |
ω |
r |
(s) |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ωe (ω −lωb |
|
|
Всюду за исключением точки r = rb уравнение (42.6) сводится к следующему: |
|
|
1 d |
r |
|
dψ |
− |
|
l 2 |
ψ = 0 . |
|
|
|
|
|
|
|
|
|
|
|
(42.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r dr |
|
dr |
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ограниченное при r = 0 и обращающееся в ноль при r = R решение уравнения (42.7) дается

Александров А.Ф., Кузелев М.В. Физика электронных пучков
формулами
Arl , |
− R2l r−l ), |
0 < r < rb , |
|
ψ (r) = B(rl |
r < r < R, |
(42.8) |
|
|
b |
|
где А и В – постоянные. В дальнейшем будем рассматривать только случай l =1 . Напомним также, что частота Ωe , в соответствии с (22.6), знака заряда не содержит.
Для исключения постоянных А и В найдем условия сшивки потенциала на границе плазмы. Одно условие очевидно сводится к непрерывности самого потенциала
ψ (rb + 0) −ψ (rb − 0) = 0 . |
|
|
|
|
|
|
|
|
|
(42.9) |
Второе - получается интегрированием уравнения (42.6) по rdr |
в окрестности границы плаз- |
мы r = rb , что дает следующее: |
|
|
|
|
|
|
|
|
|
|
|
dψ (rb + 0) |
|
2 |
|
− 0) |
1 |
|
|
|
2 |
|
|
|
|
ωLi dψ (rb |
ψ (rb ) |
|
|
ωLb |
|
|
|
− 1 − |
ω2 |
|
|
|
= |
|
|
|
|
. |
(42.10) |
|
dr |
|
dr |
|
r |
Ω |
e |
(ω −ω(s) ) |
|
|
|
|
|
|
|
b |
|
|
b |
|
Подставляя решения (42.8) в условия (42.9) и (42.10) и исключая постоянные А и В, получим дисперсионное уравнение для определения собственных частот ω
1 |
= f |
m ω2 |
− |
|
ω2 |
. |
(42.11) |
1− (r R)2 |
Lb |
2Ω |
Lb |
|
M 2ω2 |
|
(ω −ω(s) ) |
|
|
b |
|
|
|
e |
b |
|
|
Здесь была учтена связь между ионной и электронной ленгмюровской частотами. При малой плотности электронов пучка (см. (23.12) и второе неравенство (42.2)) выражение для угловой скорости вращения пучка ωb(s) упрощается
ωb(s) = ωb(−) = |
|
ω2 |
(1 − f |
− β02 ) . |
|
|
|
|
|
(42.12) |
|
Lb |
|
|
|
|
|
|
2Ωe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для анализа уравнения (42.11) введем следующие безразмерные величины: |
y = |
ω |
, |
x = |
ω2 |
|
(1 − f − β 2 ), p |
= |
1 − (r R)2 |
, |
(42.13) |
Ωe |
Lb |
|
1− f |
b |
− β02 |
|
|
|
|
2Ωe2 |
|
0 |
|
|
|
|
причем ограничимся случаем 1 − f − β02 |
> 0 и |
|
p <<1 (при больших |
p анализ дисперсионно- |
го уравнения довольно сложен). В новых переменных дисперсионное уравнение записывается в виде
|
y2 (y − x(1 − p))= f |
m |
xp( y − x) = 0 . |
(42.14) |
|
M |
|
|
|
|
Вуравнении (42.14) присутствует малый параметр f m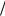 M (для водородной плазмы m
M (для водородной плазмы m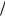 M ≈
M ≈
5.410−4 ). В нулевом приближении по этому параметру (или при f = 0 ) из (42.14) находим три корня
y1 = x(1 − p), y2,3 = 0 . |
(42.15) |

Александров А.Ф., Кузелев М.В. Физика электронных пучков
Первый корень, после перехода к размерным переменным, дает ω ≈ ωLb2 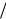 2Ωe и описывает дрейфовое вращение пучка в скрещенных внешнем магнитном и собственном электрическом полях. Именно корень y1 порождает комплексные решения уравнения (42.14).
2Ωe и описывает дрейфовое вращение пучка в скрещенных внешнем магнитном и собственном электрическом полях. Именно корень y1 порождает комплексные решения уравнения (42.14).
Делая замену |
|
|
|
|
|
|
|
|
|
|
|
y = y1 + z , |
|
|
|
|
|
|
|
|
|
|
|
(42.16) |
в низшем по параметру |
|
f m M порядке и с учетом неравенства |
p <<1, преобразуем уравне- |
ние (42.14) к виду |
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 + |
1 |
xz |
|
+ |
1 |
f |
|
m |
|
p2 x = 0 . |
|
|
|
|
(42.17) |
|
|
|
|
|
M |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Решая квадратное уравнение (42.17), находим |
|
z |
|
= − |
1 |
|
x ± |
1 |
x |
1−8 f |
|
m p2 |
|
|
(42.18) |
|
|
|
|
|
|
|
. |
|
|
1,2 |
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
M |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неустойчивость имеет место при выполнении неравенства |
|
x < 8 f |
|
m |
|
|
p2 . |
|
|
|
|
|
|
|
|
|
|
(42.19) |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимум инкремента достигается при |
|
|
|
x = 4 f |
m |
p2 . |
|
|
|
|
|
|
|
|
|
|
(42.20) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
В безразмерном виде максимальный инкремент неустойчивости дается формулой |
Im z = f |
|
m |
p2 |
. |
|
|
|
|
|
|
|
|
(42.21) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
В размерных переменных условие (42.19) возникновения неустойчивости имеет вид |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
02 ) < 8 f m |
|
|
2 |
2 |
(42.22) |
ωLb2 (1 − f − β |
1 |
− |
(rb R)2 |
|
, |
2Ωe |
|
|
|
|
|
|
|
|
|
|
|
M |
1 − f − β0 |
|
|
|
а комплексная частота с максимальной мнимой частью определяется следующим выражением
ω = (3 + i)Ωe f |
m |
|
|
− (rb |
2 |
2 |
= (3 + i) |
2 |
(42.23) |
1 |
R)2 |
|
ωLb (1 − f − β02 ) . |
|
M |
|
1 − f − β0 |
|
|
2Ωe |
|
Видно, что действительная и мнимая части частоты имеют одинаковый порядок, т.е. рассмотренная неустойчивость является апериодической. Максимальный инкремент этой электрон – ионной неустойчивости совпадает с частотой (42.12) дрейфового вращения. Отноше-
ние масс m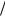 M определяет область плотностей пучка, в которой существует неустойчивость:
M определяет область плотностей пучка, в которой существует неустойчивость:
при m M → 0 , или при f = 0 , размер области неустойчивости равен нулю.
M → 0 , или при f = 0 , размер области неустойчивости равен нулю.
Рассмотренную неустойчивость называют также токово-конвективной. При этой не-
Александров А.Ф., Кузелев М.В. Физика электронных пучков
устойчивости, поскольку она развивается на азимутально несимметричных модах с l ≥1, электронный пучок ассиметрично смещается относительно нейтрализующего ионного фона. Дрейфовое вращение пучка приводит к апериодическому нарастанию величины данного смещения, т.е. к уходу электронного пучка от его равновесного положения внутри нейтрализующего ионного канала.
§ 43. Неустойчивости пучка с неоднородным поперечным профилем продольной скорости - slipping-неустойчивости
Предположим, что зарядовая нейтрализация электронного пучка обеспечивается фоном бесконечно тяжелых ионов, электроны фона отсутствуют, а продольная скорость элек-
тронов пучка Vbz(s) ≡ u(r) зависит от поперечной координаты r. Неустойчивости, которые рас-
сматриваются в данном разделе связаны именно с неоднородностью поперечного распределения продольной скорости направленного движения электронов пучка.
Начнем со случая отсутствия внешнего магнитного поля, т.е. Ωe = 0 . Пучок считаем нерелятивистским и полностью нейтрализованным ионным фоном. Тогда, согласно формуле
(23.8), записанной для f =1 и β02 → 0 , угловая скорость азимутального вращения пучка рав-
на нулю. При этом общее дифференциальное уравнение (40.18) сводится к следующему виду:
|
1 d |
rε(r) |
dψ |
− |
l 2 |
|
ε(r)ψ − k 2ε(r)ψ = 0 , |
(43.1) |
|
|
|
|
|
|
|
r dr |
dr |
r2 |
|
|
|
|
|
z |
|
где |
|
|
|
|
|
|
|
|
|
ε(r) =1 − |
|
ωLb2 (r) |
|
. |
(43.2) |
(ω − kzu(r))2 |
Для некоторых специально подобранных функций ε(r) |
уравнение (43.1) удается решить |
аналитически. Мы, чтобы установить сам факт существования новой для нас неустойчивости, ограничимся случаем ступенчатой функции ε(r) .
Пусть распределения плотности и скорости электронов пучка определяются форму-
лами
ωLb2 (r) = |
ω2 |
, |
r < a |
, |
u |
, |
r < a |
, |
(43.3) |
Lb1 |
, |
r > a |
u(r) = |
1 |
, |
r > a |
|
|
ω2 |
|
u |
2 |
|
|
|
|
Lb2 |
|
|
|
|
|
|
|
|
где ω2 |
и u |
- постоянные. В областях r < a и r > a уравнение (43.1) можно сократить на |
Lb1,2 |
1,2 |
|
|
|
|
|
|
|
|
|
|
постоянную величину ε(r) и записать его решение в виде (полагаем конечно, что ε(r) ≠ 0 )








 2
2