
Начало возможных перемещений
Начало возможных перемещений, являясь общим принципом механики, имеет важнейшее значение для теории упругих систем. Применительно к ним этот принцип можно сформулировать следующим образом: если система находится в равновесии под действием приложенной нагрузки, то сумма работ внешних и внутренних сил на возможных бесконечно малых перемещениях системы равна нулю.
![]() , (2.2.13)
, (2.2.13)
где
![]() - внешние силы;
- внешние силы;![]() - возможные перемещения этих сил;
- возможные перемещения этих сил;![]() - работа внутренних сил.
- работа внутренних сил.
Заметим, что в процессе совершения системой возможного перемещения величина и направление внешних и внутренних сил остаются неизменными. Поэтому при вычислении работ следует брать на половину, а полную величину произведения соответствующих сил и перемещений.
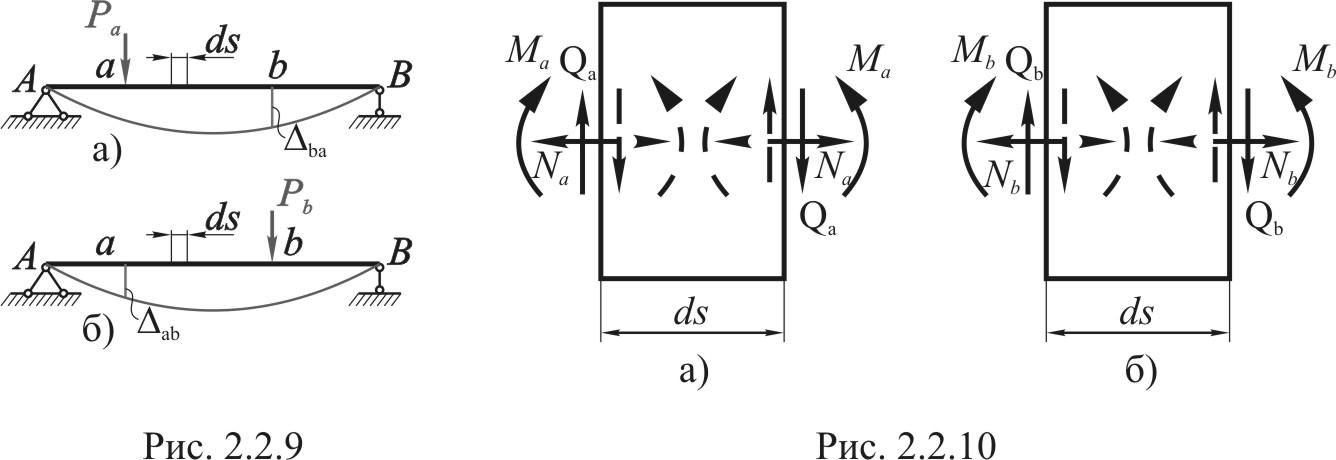
Рассмотрим два состояния какой-либо
системы, находящейся в равновесии (рис.
2.2.9). В состоянии
![]() система деформируется обобщенной силой
система деформируется обобщенной силой![]() (рис. 2.2.9, а), в состоянии
(рис. 2.2.9, а), в состоянии![]() - силой
- силой![]() (рис. 2.2.9, б).
(рис. 2.2.9, б).
Работа сил состояния
![]() на перемещениях состояния
на перемещениях состояния![]() ,
как и работа сил состояния
,
как и работа сил состояния![]() на перемещениях состояния
на перемещениях состояния![]() ,
будет возможной.
,
будет возможной.
![]() (2.2.14)
(2.2.14)
Вычислим теперь возможную работу
внутренних сил состояния
![]() на перемещениях, вызванных нагрузкой
состояния
на перемещениях, вызванных нагрузкой
состояния![]() .
Для этого рассмотрим произвольный
элемент стержня длиной
.
Для этого рассмотрим произвольный
элемент стержня длиной![]() в обоих случаях. Для плоского изгиба
действие удаленных частей на элемент
выражается системой усилий
в обоих случаях. Для плоского изгиба
действие удаленных частей на элемент
выражается системой усилий![]() ,
,![]() ,
,![]() (рис. 2.2.10, а). Внутренние усилия имеют
направления, противоположные внешним
(показаны штриховыми линиями). На рис.
2.2.10, б показаны внешние усилия
(рис. 2.2.10, а). Внутренние усилия имеют
направления, противоположные внешним
(показаны штриховыми линиями). На рис.
2.2.10, б показаны внешние усилия![]() ,
,![]() ,
,![]() ,
действующие на элемент
,
действующие на элемент![]() в состоянии
в состоянии![]() .
Определим деформации, вызванные этими
усилиями.
.
Определим деформации, вызванные этими
усилиями.
Очевидно удлинение элемента
![]() ,
вызванное силами
,
вызванное силами![]()
![]() .
.
Работа внутренних осевых сил
![]() на этом возможном перемещении
на этом возможном перемещении
![]() . (2.2.15)
. (2.2.15)
Взаимный угол поворота граней элемента,
вызванный парами
![]() ,
,
![]() .
.
Работа внутренних изгибающих моментов
![]() на этом перемещении
на этом перемещении
![]() . (2.2.16)
. (2.2.16)
Аналогично определяем работу поперечных
сил
![]() на перемещениях, вызванных силами
на перемещениях, вызванных силами![]()
![]() . (2.2.17)
. (2.2.17)
Суммируя полученные работы, получаем
возможную работу внутренних сил,
приложенных к элементу
![]() стержня, на перемещениях, вызванной
другой, вполне произвольной нагрузкой,
отмеченной индексом
стержня, на перемещениях, вызванной
другой, вполне произвольной нагрузкой,
отмеченной индексом![]()
![]() (2.2.18)
(2.2.18)
Просуммировав элементарные работы в пределах стержня, получим полное значение возможной работы внутренних сил:
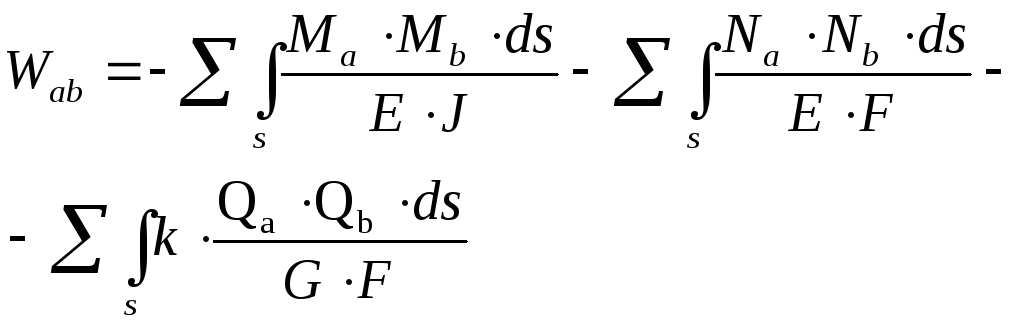 (2.2.19)
(2.2.19)
Применим начало возможных перемещений, суммируя работу внутренних и внешних сил на возможных перемещениях системы, и получим общее выражение начала возможных перемещений для плоской упругой стержневой системы:
 (2.2.20)
(2.2.20)
Т. е., если упругая система находится в
равновесии, то работа внешних и внутренних
сил в состоянии
![]() на возможных перемещениях, вызванных
другой, вполне произвольной нагрузкой,
отмеченной индексом
на возможных перемещениях, вызванных
другой, вполне произвольной нагрузкой,
отмеченной индексом![]() ,
равна нулю.
,
равна нулю.
Теоремы о взаимности работ и перемещений
Запишем выражения начала возможных
перемещений для балки, показанной на
рис. 2.2.9, приняв для состояния
![]() в качестве возможных перемещения,
вызванные состоянием
в качестве возможных перемещения,
вызванные состоянием![]() ,
а для состояния
,
а для состояния![]() - перемещения, вызванные состоянием
- перемещения, вызванные состоянием![]() .
.
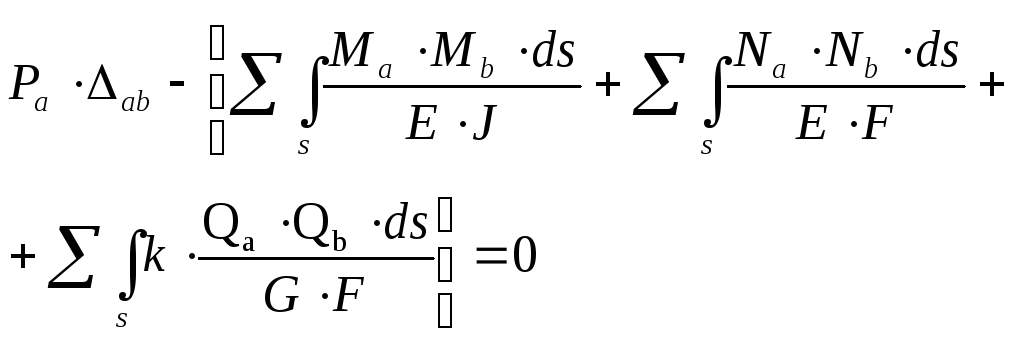 (2.2.21)
(2.2.21)
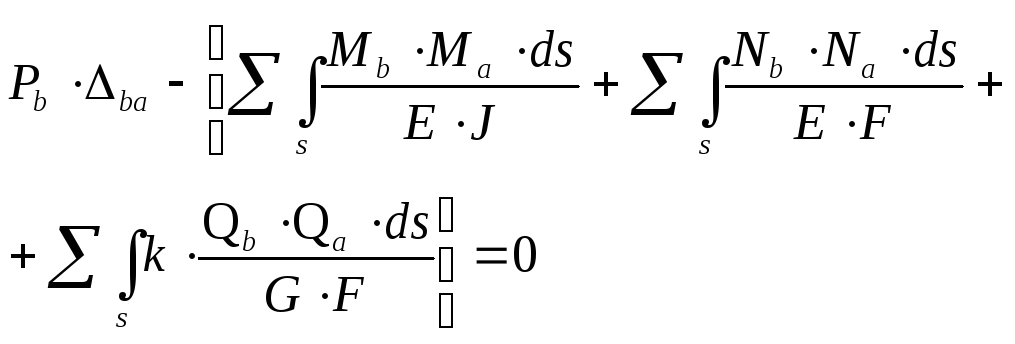 (2.2.22)
(2.2.22)
Так как выражения работ внутренних сил одинаковы, то очевидно, что
![]() (2.2.23)
(2.2.23)
Полученное выражение носит название
теоремы о взаимности работ (теоремы
Бетти). Она формулируется следующим
образом: возможная работа внешних (или
внутренних) сил состояния
![]() на перемещениях состояния
на перемещениях состояния![]() равна возможной работе внешних (или
внутренних) сил состояния
равна возможной работе внешних (или
внутренних) сил состояния![]() на перемещениях состояния
на перемещениях состояния![]() .
.
Применим теорему о взаимности работ к
частному случаю нагружения, когда в
обоих состояниях системы приложено по
одной единичной обобщенной силе
![]() и
и![]() .
.
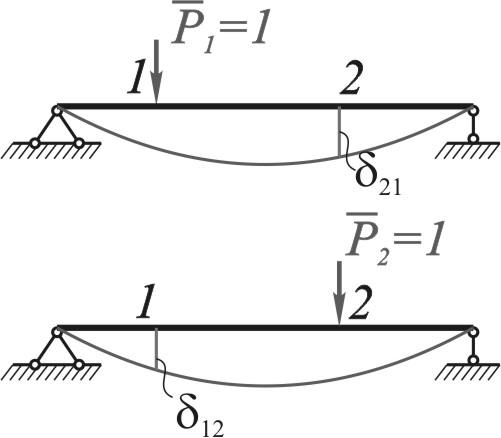
Рис. 2.2.11
На основании теоремы о взаимности работ получаем равенство
![]() , (2.2.24)
, (2.2.24)
которое носит название теоремы о взаимности перемещений (теоремы Максвелла). Формулируется она так: перемещение точки приложения первой силы по ее направлению, вызванное действием второй единичной силы, равно перемещению точки приложения второй силы по ее направлению, вызванному действием первой единичной силы.
Теоремы о взаимности работ и перемещений существенно упрощают решение многих задач при определении перемещений.
Пользуясь теоремой о взаимности работ,
определим прогиб
![]() балки посредине пролета при действии
на опоре момента
балки посредине пролета при действии
на опоре момента![]() (рис. 2.2.12, а).
(рис. 2.2.12, а).
Используем второе состояние балки –
действие в точке 2 сосредоточенной силы
![]() .
Угол поворота опорного сечения
.
Угол поворота опорного сечения![]() определим из условия закрепления балки
в точке В:
определим из условия закрепления балки
в точке В:
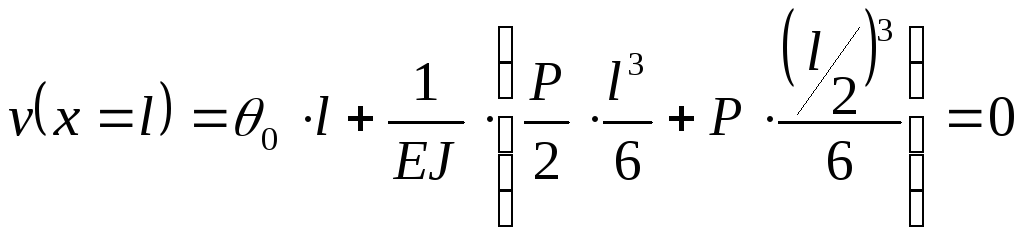
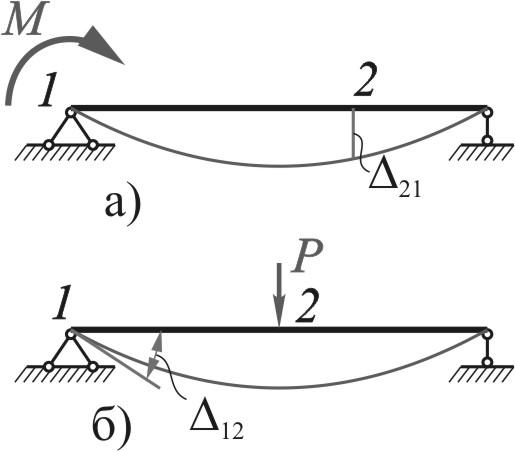
Рис. 2.2.12
![]()
Согласно теореме о взаимности работ
![]() ,
,
откуда
![]() (2.2.25)
(2.2.25)
