
Давыд Цуриков. Автореферат диссертации. 2015 г
..pdf
На правах рукописи
Цуриков Давыд Евгеньевич
МОДЕЛИРОВАНИЕ КВАНТОВОГО ЭЛЕКТРОННОГО ТРАНСПОРТА
ВРАЗВЕТВЛЁННЫХ ПОЛУПРОВОДНИКОВЫХ СТРУКТУРАХ
СПОНИЖЕННОЙ РАЗМЕРНОСТЬЮ
специальность 01.04.10 – физика полупроводников
АВТОРЕФЕРАТ
диссертации на соискание учёной степени кандидата физико-математических наук
Санкт-Петербург
2015

Работа выполнена в Санкт-Петербургском государственном университете
Научный руководитель: Яфясов Адиль Абдул Меликович
доктор физико-математических наук, профессор, профессор кафедры электроники твердого тела, СПбГУ
Официальные оппоненты: Баграев Николай Таймуразович
доктор физико-математических наук, профессор, ведущий научный сотрудник, Физикотехнический институт им. А.Ф. Иоффе РАН
Попов Игорь Юрьевич
доктор физико-математических наук, профессор, заведующий кафедрой высшей математики, Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики
Ведущая организация: Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Защита состоится 17 декабря 2015 года в 13 час. 00 мин. на заседании диссертационного совета Д.212.232.33 по защите докторских и кандидатских диссертаций при Санкт-Петербургском государственном университете по адресу: 198504, г. Санкт-Петербург, Петродворец, ул. Ульяновская д. 1, физический факультет СПбГУ, малый конференц-зал.
С диссертацией можно ознакомиться в научной библиотеке им. М. Горького СПбГУ по адресу: 199034, г. Санкт-Петербург, Университетская наб., д. 7/9. Диссертация и автореферат размещены на сайте www.spbu.ru.
Автореферат разослан «___» _________ 2015 г. |
|
Ученый секретарь |
|
диссертационного совета, |
|
к.ф.-м.н., доцент |
Поляничко А.М. |
3
Общая характеристика работы
Актуальность темы
Движущим фактором развития современной вычислительной техники является полупроводниковая наноэлектроника. Наноэлектроника занимается созданием и исследованием приборов, для которых существенны эффекты размерного квантования. Моделированию квантового электронного транспорта в низкоразмерных полупроводниковых структурах посвящено множество работ. Несмотря на это, совершенствование схемы его расчёта по-прежнему является актуальным.
На сегодняшний день особо интересны наноэлектронные устройства на базе двумерного газа носителей заряда. Поэтому, помимо расчёта транспортных свойств низкоразмерных структур, актуален комплексный численный анализ процесса их формирования в полупроводниковых плёнках.
Степень разработанности темы
Диссертация разделена на три самостоятельные, но логически взаимосвязанные главы. Обзор современного состояния исследований проводится в каждой из них.
Цель и задачи
Цель данной работы – совершенствование методики численного моделирования квантового электронного транспорта в низкоразмерных полупроводниковых структурах. Центральная задача в её рамках – разработка объединённой схемы расчёта электрических токов в модели квантовой сети. Схема тестируется в проектировании наноустройств на базе двумерного электронного газа. Предварительно для этого рассматривается процесс двумеризации носителей заряда в полупроводниковой плёнке.
Научная новизна
Научная новизна полученных в работе результатов определяется согласно поставленным задачам численного моделирования.
1.Двумеризация носителей заряда. В рамках моделирования процесса двумеризации носителей заряда в полупроводниковой плёнке сформулирован быстрый алгоритм квантового самосогласованного расчёта области пространственного заряда.
2.Квантовый электронный транспорт. В рамках моделирования квантового электронного транспорта в низкоразмерных полупроводниковых структурах предложена специальная схема расчёта. Она основана на объединении адаптированных методов в эффективной системе обозначений. Помимо удобства в реализации на ЭВМ, схема обладает наглядностью, что упрощает моделирование низкоразмерных структур со сложной геометрией.
3.Двумерные наноустройства. В настоящей работе предложены три модели полупроводниковых устройств на базе двумерного электронного газа. В модели логического элемента NOT в двумерном электронном волноводе была достигнута рав-

4
ная 97% вероятность рассеяния электронов из 1-й подзоны размерного квантования во 2-ю. При проектировании двухузлового переключателя установлено, что эффективно изменять направление токов в двумерной структуре можно с помощью латерального затвора, предшествующего области ветвления. Моделирование логического элемента XOR продемонстрировало выполнение логической операции напрямую за счёт квантовой интерференции. Исходя из аналогии с искусственными нейронными сетями, на примере данного устройства установлено, что низкоразмерные полупроводниковые структуры способны к обучению.
Научная и практическая значимость работы
•Научная значимость работы состоит в совершенствовании методики численного моделирования квантового электронного транспорта в низкоразмерных полупроводниковых структурах.
•Практическая значимость работы состоит в том, что предложенная схема расчёта упрощает моделирование всевозможных наноэлектронных устройств.
Методы исследования
Методы исследования, используемые в данной работе (табл. 1), реализованы в виде программного кода на языке C++, а также процедур в пакете FreeFem++.
Таблица 1. Основные методы численного исследования в диссертации
глава |
задача |
методы решения |
|
|
|
1 |
квантовый самосогласованный расчёт |
метод последовательных |
|
области пространственного заряда |
приближений |
|
расчёт расширенной матрицы рассеяния |
граничные условия рассеяния, |
|
узла квантовой сети |
ND-map |
|
|
|
2 |
расчёт расширенной матрицы рассеяния |
формула объединения, |
|
квантовой сети |
сетевая формула |
|
расчёт электрических токов |
формализм Ландауэра–Бюттикера |
|
через квантовую сеть |
|
|
|
|
|
|
|
3 |
оптимизация параметров |
генетический алгоритм |
|
электронных наноустройств |
|
Достоверность результатов
Достоверность развиваемого в работе подхода подтверждается посредством моделирования наноустройств на базе двумерного электронного газа. Предварительно для этого с помощью квантового самосогласованного расчёта изучается процесс двумеризации носителей заряда в полупроводниковой плёнке. Достоверность его результатов подтвердилась вычислениями дифференциальной ёмкости плёнки [4].
5
Для предложенных в работе моделей наноустройств можно отметить реалистичность конструкционных решений, протекающих через них электрических токов и оптимизированных напряжённостей электрического поля. Контроль ошибки расчётов осуществлялся параллельно двумя способами. В основе первого способа было сравнение вероятностей рассеяния, полученных на основе оригинальной схемы и путём триангуляции всей структуры. В основе второго – выполнение закона сохранения заряда. В обоих случаях погрешность оставалась на приемлемом уровне.
Апробация результатов
Материалы диссертации были представлены на следующих конференциях.
1.Tsurikov D., Pavlov B., Yafyasov A., Semenikhin I. Scattering on a Junction: Analytic Perturbation Procedure and Direct Computing; Poster: Conference, Amherst, USA; 10- 08-2007 – 10-10-2007; in: "Proc. of IWCE". 2007. P. 74–75.
2.Цуриков Д. Е. Дифференциальная ёмкость многослойной полупроводниковой структуры. Тезисы конференции «Физика и прогресс». 2007. С. 106.
3.Tsurikov D. Combining formula for calculation of quantum network S-matrix. Conference Abstracts, International Student Conference “Science and Progress”, St. Petersburg. 2010. P. 106.
4.Tsurikov D. The “closed-channel” property of extended current S-matrix of junction. Conference Abstracts, International Student Conference “Science and Progress”, St. Petersburg. 2011. P. 126.
Защищаемые положения
1.Алгоритм квантового самосогласованного расчёта области пространственного заряда в однородно легированной полупроводниковой плёнке.
2.Расчёт расширенной матрицы рассеяния узла квантовой сети с помощью граничных условий рассеяния в интегро-дифференциальной формулировке.
3.Формула для расширенной матрицы рассеяния квантовой сети в терминах расширенных матриц рассеяния её узлов.
4.Квантовая сеть из гладких Q-, I- и Y-узлов как основа для моделирования полупроводниковых наноустройств на базе двумерного электронного газа.
5.Модели полупроводниковых наноустройств на базе QIY-сети, выполняющих следующие функции:
•логическую операцию NOT за счёт инверсии потоков вероятностей в каналах с помощью латерального затвора в I-структуре;
•переключение электрических токов в Y-структуре с помощью латерального затвора в малой области перед ветвлением;
•логическую операцию XOR за счёт управления проводимостью гексагональной структуры с помощью латеральных затворов.
6
Структура и объём диссертации
Диссертация состоит из введения, трёх глав, заключения, восьми приложений и списка литературы. Она содержит 32 рисунка и 27 таблиц, её объём составляет 155 страниц. Список литературы включает 73 наименования.
Содержание работы
Введение
Во введении отражена актуальность темы диссертации, указаны её цели и задачи, научная новизна, научная и практическая значимость. Также в нём перечислены основные методы исследования, обоснована достоверность полученных результатов, приведён перечень защищаемых положений.
Глава 1. Размерное квантование в полупроводнике
Глава 1 состоит из обзорного раздела 1.1 и раздела 1.2, в котором представлен оригинальный алгоритм квантового самосогласованного расчёта области пространственного заряда (ОПЗ) в однородно легированной полупроводниковой плёнке [4].
1.1. Низкоразмерные структуры
В этом обзорном разделе даны основные понятия, связанные с размерным квантованием носителей заряда в полупроводниках. Помимо используемых в расчётах приближений (подраздел 1.1.1) здесь приведена классификация низкоразмерных кристаллических структур (подраздел 1.1.2). На основе неё указаны минимальный и максимальный размеры рассматриваемых в работе систем.
1.2. Двумеризация носителей заряда в плёнке
Вэтом разделе предложен алгоритм квантового самосогласованного расчёта ОПЗ
вполупроводниковой плёнке в случае омического контакта с металлом на тыльной стороне (рис. 1). Он основан на совместном решении уравнений Шрёдингера и Пуассона. Повышение его скорости и устойчивости достигается следующим образом:
• расчёт уровня Ферми на основе уравнения электронейтральности без самосогласования;
• при каждом значении поверхностного потенциала VS расчёт для электронов и ды-
рок только тех уровней энергии, которые существенно влияют на заряд в ОПЗ;
•выход из самосогласованной процедуры при достижении заданной точности расчёта поверхностной плотности заряда в ОПЗ;
•расчёт уровней энергии на основе метода стрельбы для задачи Коши с учётом правила формального смещения границы плёнки, с применением алгоритма Верле в скоростной форме на сетке с постоянным шагом;
7
• локализация уровней энергии на основе параболической экстраполяции. Квантовый самосогласованный расчёт ОПЗ реализован в виде программного кода
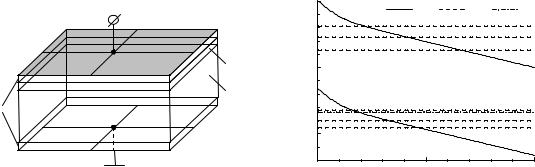
на языке C++. С его помощью смоделирована плёнка собственного германия (111) при T = 300 K , показан принцип позиционирования уровня Ферми в энергетическом спектре носителей заряда посредством верхнего затвора (рис. 2). Поэтому ниже при проектировании устройств на базе двумерного электронного газа (глава 3) предполагалось, что уровень Ферми можно установить наперёд заданным образом.
top gate |
|
0,5 |
1 |
2 |
3 |
|
|
||||
|
|
|
|
|
|
2 |
E, eV |
0,0 |
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
-0,5 |
|
|
|
|
|
0 |
10 |
|
20 |
|
|
|
Z, nm |
|
|
Рис. 1. Полупроводниковая плёнка |
Рис. 2. Энергетическая структура плёнки соб- |
||||
в структуре с верхним затвором: |
ственного германия L = 20 нм, VS |
= −0.5 В: |
|||
1 – металл, 2 – диэлектрик, 3 – по- |
1 – потенциал для электронов (вверху) и дырок |
||||
лупроводник. Лицевая сторона |
(внизу), 2 – первые три уровня энергии элек- |
||||
вверху, тыльная внизу. L – тол- |
тронов (вверху) и дырок (внизу), 3 – уровень |
||||
щина плёнки. |
Ферми. |
|
|
|
|
Глава 2. Электронный транспорт в низкоразмерных структурах
Глава 2 состоит из трёх разделов: обзор литературы представлен в разделе 2.1, оригинальный материал – в разделах 2.2 и 2.3.
2.1. Моделирование разветвлённых низкоразмерных структур
В этом обзорном разделе введено понятие квантовой сети как математической модели для описания электронного транспорта в разветвлённых низкоразмерных структурах. Указано, что для расчёта токов через сеть в формализме Ландауэра– Бюттикера следует найти её матрицу рассеяния. Рассмотрены следующие методы расчёта матрицы рассеяния: граничные условия рассеяния, формализм DN- и NDmap, формализм R-матрицы, объединение матриц рассеяния узлов. Для каждого из них указаны преимущества и недостатки. Отмечено, что различия в обозначениях разных работ усложняют реализацию расчётов на ЭВМ. Сделан вывод об актуальности создания схемы расчётов, основанной на объединении адаптированных методов в эффективной системе обозначений.
8
2.2. Рассеяние электрона в квантовой сети
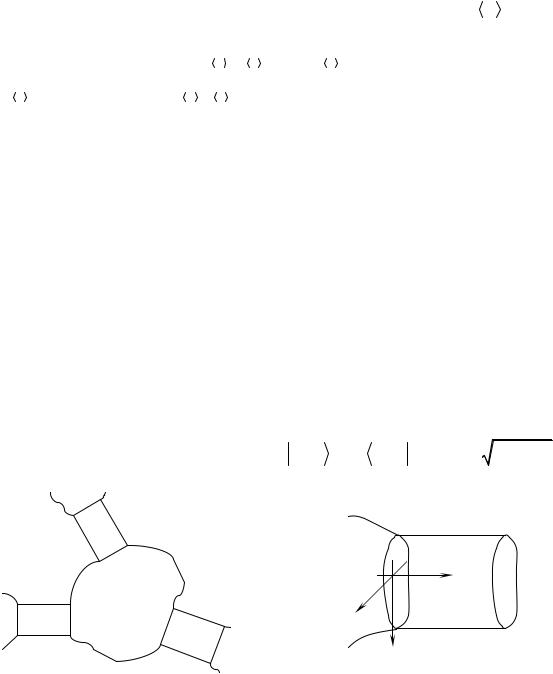
В разделе 2.2 проведена последовательная формализация задачи рассеяния электрона в кантовой сети. Для упрощения математических рассуждений и повышения их наглядности в подразделе 2.2.1 введена оригинальная система соглашений и обозначений [3]. Обозначения основаны на нумерации рукавов сети (рис. 3). Наряду с «рукавными» идентификаторами [...] также используются «узловые» ... , в частности, для конкретизации структуры сети перечислением:
{Ω[K] = Ω A | a A = a[K] , b A = b[K] ,...}K A |
(1) |
где Ω A – узел типа «A», a A ,b A ,... – параметры узла типа «A», {a[K] ,b[K] ,...}K A – значения параметров узлов типа «A» в сети, A – упорядоченный набор (кортеж) «рукавных» идентификаторов узлов типа «A» в сети.
Постановка задачи дана в подразделе 2.2.2. Здесь проведён переход от размерного уравнения Шрёдингера к безразмерному:
(− +υ)Ψ =εΨ |
(2) |
С помощью локальных систем координат (ЛСК, рис. 4) записана волновая функция электрона в рукаве Ωk в ЛСК [XYZ ][A]k в виде суммы падающих и рассеянных волн:
ψ[A]k =ψ[A] k +ψ[A] k , ψ[A] k := ∑mψm[A] k , |
ψ[A] |
k := ∑mψm[A] k |
(3) |
|
ψm[A] k (x, y, z):= exp(−iK[A] x)c[A] |
k |
|
k |
|
m hm[A]k (y, z)= exp(−iK[A] x)h[A] (y, z) m cm[A] k |
(4) |
|||
ψm[A] k (x, y, z):= exp(+iK[A] x)c[A] |
k |
|
k |
|
|
|
|||
m hm[A]k (y, z)= exp(+iK[A] x)h[A] (y, z) m cm[A] k |
|
|||
Kmn[A]kl := Imn[A]klκm[A]k , K[A]kl := I[A]kl ∑n hn[A]k κn[A]k |
hn[A]k , |
κm[A]k := ε −λm[A]k |
(5) |
|
|
Ω2 |
|
|
Ω[A] |
|
|
Γ[A]2 |
|
Ωk |
|
|
|
|
|
|
|
[A] |
|
X [A]k |
|
|
Ω |
|
|
Ω1 |
Γ[A]1 |
Γ[A]k |
Ωk |
Y[A]k |
|
|
|
|
Z[A]k |
Рис. 3. Участок квантовой сети: Ω[A] – узел, |
Рис. 4. Рукав Ωk с локальной системой |
|||
A N ; Ωk |
– k-й рукав, k A . |
координат [XYZ ][A]k на границе Γ[A]k . |
||
Следующим шагом были сформулированы задачи рассеяния двух типов:
•входная задача рассеяния – поиск рассеянных волн по известным падающим;
•выходная задача рассеяния – поиск падающих волн по известным рассеянным.
9
Указано, что амплитуды падающих и рассеянных волн с учётом всех каналов связы-
вает расширенная матрица рассеяния (extended scattering matrix) S[A] узла Ω[A] :
cm[A] k = ∑ln Smn[A]klcn[A] l |
(6) |
Всюду в оригинальных разделах работы этот объект именуется кратко: S-матрица. Подраздел 2.2.3 посвящён расчёту S-матрицы узла квантовой сети. Для краткости
в нём редуцирован идентификатор узла. В качестве основного метода предложены граничные условия рассеяния (ГУР) в интегро-дифференциальной формулировке [1]. Для входной и выходной задач в ЛСК они записаны в виде:
[− +υ]Ψ =εΨ |
in Ω |
[− +υ]Ψ =εΨ |
in Ω |
|
||
|
|
on ∂Ω \ Γ, |
|
|
on ∂Ω \ Γ |
(7) |
Ψ = 0 |
|
Ψ = 0 |
|
|||
|
]W Ψ = 2Kψ |
on γ |
|
]W Ψ = 2Kψ on γ |
|
|
[K +i∂1 |
[K −i∂1 |
|
||||
Далее показано, как с помощью входных ГУР можно найти поэлементно S- матрицу узла. Указано, что в случаях, когда в одном из двух эквивалентных представлений можно ввести оператор G◊ :
|
◊ |
(x)c |
◊ k k |
|
|
k |
Ψ(x, y, z)=: |
|
◊k |
◊ |
k |
(8) |
||||||
∑m G |
|
m hm (y, z):=W |
|
|
∑m cm |
G |
|
(x)h(y, z) m |
||||||||||
S-матрица записывается в явном виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
S =G |
◊ |
|
|
◊ |
(0) −G |
◊ |
(0) |
|
−1 |
i2K |
− I |
|
|
(9) |
|
|
|
|
|
(0) iKG |
|
|
|
|
|
|
|
|||||||
Этот формализм позволил установить связь метода ГУР с методами DN- и ND-map. Они также рекомендованы как альтернатива ГУР, так как не все вычислительные пакеты поддерживают интегро-дифференциальные граничные условия.
Наконец, было показано, что в терминах нулевых входных и выходных ГУР для узла можно наглядно записать задачи на полюсы и нули S-матрицы: ε+ , ε− (резонансы и связанные состояния, антирезонансы и антисвязанные состояния). В глобальной системе координат (ГСК) они записаны в виде:
|
|
|
|
± |
=ε |
± |
Ψ |
± |
in Ω |
|
|
[− +υ]Ψ |
|
|
|
(10) |
|||||||
Ψ± = 0 |
|
|
|
|
|
|
|
on ∂Ω\ Γ |
|||
|
± |
±i∂n |
]Ψ |
± |
= 0 |
|
on Γ |
|
|||
[K |
|
|
|
|
|||||||
Когда в сравнении с K ± оператор ∂n |
пренебрежимо мал, эти задачи переходят в зада- |
||||||||||
чу с нулевыми условиями Дирихле, которая описывает изолированный узел. Поэтому
втерминах ГУР физический смысл оператора K – изолированность узла.
Вподразделе 2.2.4 предложена сетевая формула – формула расчёта S-матрицы квантовой сети в терминах S-матриц образующих её узлов [3]:
A N |
(11) |
|
S[E] = |
S[A] |
|
где E – кортеж номеров внешних рукавов, |
N – кортеж идентификаторов внутрен- |
|
них узлов. Операция объединения S-матриц двух узлов

10
S[A] S[B] := S[A\B,B\A]
определяется на основе формулы объединения при J = A \ B, K = A∩B,
|
[J,K]JJ |
|
JL |
|
|
[J,K]JK |
|
JK |
|
|
|
|
|
|||||
S[J,L] = S |
|
O |
|
+ S |
|
|
|
|
O |
|
|
× |
|
|
|
|||
|
OLJ S[K,L]LL |
|
OLK S[K,L]LK |
|
|
|
|
|||||||||||
|
|
|
−S[J,K]KK |
|
|
|
|
|
U [J,K]KK exp(−iK KK AKK ) −1 |
S[J,K]KJ |
||||||||
× |
|
[K,L]KK |
exp(−iK |
KK |
|
KK |
) |
|
|
|
|
[K,L]KK |
|
|
OKJ |
|||
|
|
|
|
|
|
−S |
|
|||||||||||
U |
|
|
A |
|
|
|
|
|
|
|
|
|||||||
(12)
L = B\ A :
(13)
OKL
S[K,L]KL
Существенной особенностью сетевой формулы является то, что она записана в терминах расширенных матриц рассеяния. Это позволяет учесть туннельные эффекты между узлами. Также формула содержит в явном виде длины рукавов, что особенно важно при проектировании сетей с предопределёнными транспортными свойствами.
2.3. Квантовый электронный транспорт
Изложенный в разделе 2.2 подход позволил эффективно рассчитывать рассеивающие свойства низкоразмерных полупроводниковых структур в модели квантовой сети. Следующим шагом в подразделе 2.3.1 последовательно вводится понятие рас-
ширенной потоковой матрицы рассеяния C :
C = K +1/2SK −1/2 |
(14) |
а также потоковой матрицы рассеяния C++ – блока матрицы C , отвечающего за связь между открытыми каналами. Указано, что квадраты модулей элементов матрицы C++ имеют вероятностную интерпретацию.
В подразделе 2.3.2 для расчёта электрических токов через квантовую сеть предложен формализм Ландауэра–Бюттикера, адаптированный к используемой системе обозначений. Проведён вывод выражения для безразмерного тока в k-м внешнем рукаве как среднего значения по статистическому ансамблю носителей заряда:
|
Ιk = ∑lmn ∫−∞+∞ dε[λmk <ε] |
|
Cmnkl (ε) |
|
2 [ε > λnl ]{F−1 ([εFl −ε] / μl )− F−1 ([εFk −ε] / μk )} (15) |
||
|
|
|
|||||
|
|
|
|||||
где |
λk – безразмерная энергия m-го канала в k-м рукаве, F |
(η) =1/ (1+e−η ) – инте- |
|||||
|
m |
−1 |
|
||||
грал Ферми–Дирака порядка –1, εFk |
и μk – безразмерные уровень Ферми и темпера- |
||||||
тура k-го резервуара (внешнего рукава). При малых напряжениях смещения между резервуарами U kl := (EFk − EFl ) / e и их равной температуре μ= получено линейное вы-
ражение для тока в k-м внешнем рукаве в |
терминах приближённой проводимости σ : |
|||||||||
|
|
|
J k ≈ ∑l σklU lk , |
σkl := πe2 ∑mn Pmnkl |
(16) |
|||||
Pmnkl := |
1 |
|
∫−∞+∞ dε[λmk <ε] |
|
Cmnkl |
(ε) |
|
2 [ε > λnl ]ch−2 ([εF −ε] / [2μ= ]) |
(17) |
|
|
|
|
||||||||
4μ |
= |
|||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
где εF – безразмерный уровень Ферми квантовой сети при отсутствии напряжений на резервуарах.
