1. Метрика — функция, определяющая расстояния в метрическом пространстве.Множество М называется метрическим пространством, если каждой паре его элементов x и y поставлено в соответствие неотрицательное число ρ(x, y) , удовлетворяющее условиям:

[ M1] ρ (x, y) = 0 тогда и только тогда, когда x = y [аксиома тождества];

[ M2 ] ρ(x, y) = ρ(y, x) [аксиома симметрии];

[ M3 ] ρ (x, y) ≤ ρ (x, z) + ρ (z, y) для любых x, y, z ∈ M [аксиома треугольника].

Часто расстояние ρ(x, y) называют просто метрикой. Элементы метри-ческого пространства принято называть точками.

Числовая прямая, R	Множество всех веще- ственных чисел	p(x, y) x y
Евклидово n - мерное про- странство, Rn	Множество всех упо- рядоченных систем из n вещественных чисел	p(x, y) (s n )2 , где k 1 x (s1,...,sn ) , y (n1,...,nn )
Пространство C a,b	Множество всех не- прерывных функций x(t) , заданных на от- резке a,b	p(x, y) max x(t) y(t) ta,b

2. Последовательность (x_n) элементов метрического пространства E называется сходящей, если существуют элемент a ϵ Eи для любого ε > 0 натуральное число m такое, что справедливо неравенствоρ(x_na) < ε.

Пусть (X,d)— метрическое пространство. Последовательность точек {x_n}(x_n ϵ X) называется сходящейся к x ϵ Xв метрике d, если для каждого ε >0 существует такой номер N>0, что для любого n>Nвыполняется d(xn ,x)< ε.

Точка x называется пределом последовательности {x_n}.

Заметим, что свойство сходимости не меняется при замене метрики на эквивалентную.

Свойства пределов и сходящихся последовательностей.

-Если предел x0 существует, то он единственен.

-Всякая подпоследовательность сходящейся последовательности сходит-ся, причем к той же точке x0 .

-Всякая сходящаяся последовательность ограничена.

3. Пусть М – метрическое пространство. Последовательность элементов {fn} из М называется последовательностью Коши или фундаментальной последовательностью, если для любого ε > 0 существует номер n0 такой, что ρ( fn , fm ) < ε для любых n, m > n0 .

Если последовательность {fn} сходится, то она обязательно является фундаментальной.

Метрическое пространство М называется полным, если всякая фундаментальная последовательность {fn} этого пространства сходится, причем предел f0 ∈ M .

Пример 2.18.

Последовательность десятичных приближений по недостатку к √2 является фундаментальной в множестве рациональных чисел Q , однако она не сходится в Q.

Пространство изолированных точек полно, т.к. в этом про-странстве фундаментальными являются только стационарные по-следовательности: {x, x,..., x,...}→ x .

Множество действительных чисел R полно.

6. Сколярное произв. В лин. Простр. Евклидовы простр. Норма, примеры.

Пусть V – действительное линейное пространство. Скалярным произведением называется функционал, удовлетворяющий следующим свойствам:

1. 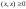, причем;

2. (z+y,z)=(x,z)+(y,z);

3. (x,y)=(y,x);

4. ,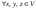и.

Линейное пространство V, наделенное скалярным произведением называется евклидовым пространством.

Всякое евклидово пространство является нормированным с нормой: 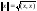. Например:

1) Для точек пространства Pⁿ x=(x₁,x₂,...,x_n) и y=(y₁,y₂,...,y_n) скалярное произведение можно определить как (x,y)=x₁*y₁+ x₂*y₂ + x_n*y_n.

2) Для функций, непрерывных на [a,b], скалярное произведение вводится по формуле

.

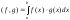4. Множество R элементов x, y, z, ... любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:

1)Существует правило, посредством которого любым двум элементам x и y множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов x и y и обозначаемый z=x+y.

2)Существует правило, посредством которого любому элементу x множества R и любому вещественному числу α ставится в соответствие элемент w этого множества, называемый произведением элемента x на число α и обозначаемый w=αx или w=xα.

3)Представленные два правила подчинены следующим восьми аксиомам:

1. x+y=y+x (переместительное свойство суммы);

2. (x+y)+z=x+(y+z) (сочетательное свойство суммы);

3. существует нулевой элемент 0 такой, что x+0=x для любого элемента x.

4. для любого элемента x существует противоположный элемент элемент x' такой, что x+x'=0;

5. 1·x=x для любого x;

6. λ(μx)=(λμ)x (сочетательное свойство относительно числового множителя);

7. (λ+μ)x=λx+μx (распределительное свойство относительно числовых множителей);

8. λ(x+y)=λx+λy (распределительное свойство относительно суммы элементов). -Совокупность линейно независимых элементов 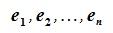пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла 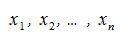такие, что выполнено равенство

Равенство называется разложением элемента x по базису а числаназываются координатами элементаx (относительно базиса ).

Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.

Размерность пространства обозначают символом dim.

Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.

Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис.

5. Нормированным векторным пространством называется векторное пространство с заданной на нем нормой.

пусть E – линейное пространство, x ├ E . Нормой эле-мента x называется функция x : E →R со свойствами (аксиомами нор-мы): 1. (норма нулевого вектора равна нулю.) 2.(норма произведения вектора на скаляр равна произведению модуля скаляра и нормы вектора.) 3.(неравенство треугольника: Норма суммы векторов не превосходит суммы их норм.)

Всякое нормированное пространство является метрическим, так как мет-рику можно ввести по формуле ρ(x, y) = x − y .

В нормированном пространстве определяетметрику. Свойства метрики и связь с нормой в нормированном пространстве: 1. если то естьто2.3.(это обычные свойства нормы и метрики и их связь в нормированных пространствах.) Метрика в нормированных пространствах обладает двумя дополнительными свойствами: 4.(инвариантность относительно сдвига) 5.(положительная однородность)

Полное нормированное векторное пространство называется банаховым пространством В.

Нормированное векторное пространство полно (т.е. является банаховым) тогда и только тогда, когда в нем всякий абсолютно схо-дящийся ряд сходится. В банаховом пространстве перестановка чле-нов абсолютно сходящегося ряда не влияет на его сумму. Для банаховых пространств всякое подмножество S ⊂ B полно тогда и только тогда, когда оно замкнуто. Таким образом, в банаховых пространствах понятие замкнутости (содержит все предельные точки) эквивалентно понятию полноты (всякая фундаментальная последовательность сходится).