4. Элементарные цифровые звенья

К числу элементарных цифровых звеньев отнесѐм:

1. Сумматор (рис. 2.3)

2. Умножитель на константу (рис. 2.4)

3. Элемент задержки (рис. 2.5)

5.Математическое описание класса операторов линейных цифровых цепей, инвариантных к сдвигу: уравнение свертки, импульсная характеристика

Цифровая цепь (ЦЦ) называется инвариантной к сдвигу, если реакция на выходе не зависит от момента воздействия. Если y(n) является реакцией на воздействие x(n), то реакцией на воздействие x(n-k) будет y(n-k). Сигнал y(n) на выходе инвариантной к сдвигу ЦЦ связан с сигналом x(n) на ее входе следующим выражением общего вида:

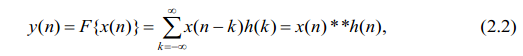
где h(k) – весовая функция, которая является импульсной характеристикой цепи. Импульсной характеристикой цепи называется еѐ реакция на единичный импульс:

Выражение (2.2) называют линейной сверткой двух временных последовательностей x(n) и h(n). Фундаментальное свойство линейных инвариантных к сдвигу ЦЦ: все свойства и характеристики цепи полностью определяются ее импульсной характеристикой, в частности, частотная характеристика H(jω) и импульсная характеристика h(n) связаны друг с другом преобразованием Фурье.

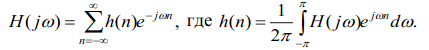
6. Устойчивость и физическая реализуемость цепей

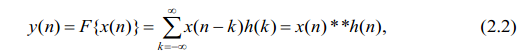
Реализация ЦЦ в форме (2.2) наталкивается на проблему устойчивости и физической реализуемости цепи. Устойчивой ЦЦ назовѐм цепь, в которой каждый ограниченный по амплитуде входной сигнал создаѐт ограниченный по амплитуде выходной сигнал. ЦЦ устойчива тогда и только тогда, когда выполняется неравенство вида

Физически реализуемая ЦЦ – это цепь, у которой изменение на выходе по времени не опережает изменение на входе. Условие физической реализуемости выполняется тогда и только тогда, когда еѐ импульсная характеристика равна нулю при всех отрицательных n (h(n)=0, для всех n<0).

7. Постановка и решение задачи аппроксимации в классе ких-цепей

Задача аппроксимации в классе КИХ-цепей: найти минимальный порядок N и импульсную характеристику h(n), цепи N-го порядка, которая, в смысле выбранного критерия близости (2.6), обеспечивает воспроизведение желаемой частотной характеристики H(ω) с заданной точностью ε_доп и весовой функцией p(ω). Решение задачи аппроксимации опирается на известную равноволновую аппроксимацию по Чебышеву, алгоритм Ремеза и программу Паркса–Мак-Клеллана.

К недостаткам класса КИХ-цепей относятся:

1. Значительный объѐм вычислительных затрат и памяти данных, обусловленный плохой сходимостью тригонометрического многочлена при решении задач аппроксимации (порядок N достигает сотни и тысячи единиц).

2. КИХ-фильтры дают постоянную задержку равную половине длины импульсной характеристики.