
учебное пособие по лр_фортран
.pdf22
№ |
Неравенство |
Неравенство |
Неравенство |
Дополнительная |
||||||||||||||||||||||
|
A |
B |
|
|
|
|
|
C |
|
логическая формула |
||||||||||||||||
16 |
x > 0 |
y > 0 |
|
y > x 2 – 2 |
A + |
|
|
|
|
|
|
|
|
|||||||||||||
B +C |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
x ≤ 0 |
y ≤ 0 |
y ≤ − |
|
x2 |
+3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A + B +C |
|||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
18 |
x > 0 |
y > 0 |
y > – x 2 + 2 |
A + |
|
|
|
|
|
|
|
|
|
|||||||||||||
B +C |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
x > 0 |
y ≤ 0 |
|
y2 |
|
−3 ≤ x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
A + B +C |
||||||||||||||||||||||||
3 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
20 |
x > 0 |
y > 0 |
|
x2 + y2 > 1 |
A + |
|
|
|
|
|
|
|
|
|
||||||||||||
|
B +C |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
21 |
x > 0 |
y ≤ 0 |
|
y > x 2 – 2 |
A + |
|
|
|
|
|
|
|
|
|||||||||||||
|
B +C |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22 |
x > 0 |
y > 0 |
|
y ≤ - x 2 + 2 |
B |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
A +C |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
23 |
x > 0 |
y > 0 |
|
x2 |
|
+ y 2 |
>1 |
B |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
A +C |
|||||||||||||||||||||||
4 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
24 |
x ≤ 0 |
y ≤ 0 |
x2 + |
y2 |
|
≤ 1 |
B |
|
|
|
|
|
|
|
|
|||||||||||
|
|
A +C |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
25 |
x > 0 |
y ≤ 0 |
|
y2 |
|
≤ x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
B A +C |
||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
26 |
x > 0 |
y ≤ 0 |
|
y ≤ x 2 – 2 |
B |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
A +C |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
27 |
x > 0 |
y ≤ 0 |
y > - x 2 + 2 |
B |
|
|
|
|
|
|
|
|
||||||||||||||
|
A +C |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
28 |
x ≤ 0 |
y ≤ 0 |
|
x2 |
|
+ y 2 |
>1 |
B |
|
|
|
|
|
|
|
|||||||||||
|
|
A +C |
||||||||||||||||||||||||
4 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
29 |
x ≤ 0 |
y > 0 |
x2 + |
y2 |
|
|
> 1 |
A + |
|
|
||||||||||||||||
|
CB |
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
30 |
x ≤ 0 |
y ≤ 0 |
|
y2 |
|
> x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
A +CB |
||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практикум по современному Фортрану
23
1.3. Построение графиков функций
Задание
1.Для каждого участка графика определить границы и составить уравнение y = fi(x).
2.Написать программу табуляции функции по участкам fi(x). Строки <аргумент><значение функции> записать в файлы Fi с расширением .txt. Для контроля и отчета создать файл Out.txt, в котором для каждого участка линии выведен заголовок и координаты не более чем 10 точек.
3.Используя приложение Advanced Grapher (далее AGrapher), вывес-
ти на экран разноцветные графики функций fi(x) из соответствующих файлов, подготовленных программой.
4.График, созданный в AGrapher, предъявить преподавателю.
Содержание отчета
1.Название работы и номер варианта индивидуального задания.
2.Фамилия, имя, отчество и номер группы студента.
3.Текст задания и график функции в том виде, как он приведен в варианте индивидуального задания.
4.Таблица участков графика (смотрите пример), в которой для каждого участка указаны границы, уравнения, шаг табуляции, количество выполнений цикла.
5.Блок – схема программы.
6.Распечатки программы и контрольного файла Out.txt.
При подготовке к защите ответить на контрольные вопросы.
Комментарии к заданию
1.Приложение Advanced GRAPHER распространяется бесплатно, ад-
рес сайта http://www.alentum.com/agrapher/. Рекомендации по работе с AGrapher смотрите в разделе 7.2.
2.Таблицу основных уравнений смотрите в разделе 7.3.
3.После разбиения графика на участки следует выбрать шаг табуляции каждого участка. Для прямолинейных участков шаг выбирается из расчета 2-5 точек на участок. На криволинейном участке с целью улучшения изображения в AGrapher шаг выбирается более мелкий, до 50 точек. Для прямой, параллельной оси Х выводятся две точки (без цикла).
4.Для табуляции каждого участка использовать оператор цикла
DO x=xn,xk,step
...
enddo
Практикум по современному Фортрану

24
Здесь х – переменная цикла; xn, xk – начальное и конечное значения x, step - шаг изменения х.
5. Количество повторений цикла рассчитывается по формуле:
|
|
xk − xn + step |
|
или |
|
|
xk − xn |
|
|
M = Max |
0, Int |
|
M = Max |
0, Int |
+1 |
||||
|
|
||||||||
|
|
step |
|
|
|
|
step |
|
|
|
|
|
|
|
|
|
Из-за применения в расчетах функции Int (преобразование в целый тип) при вещественных значениях xn, xk, step можно потерять конечное значение переменной цикла. Возможные варианты предотвращения этой ошибки:
a)при вещественных значениях xn, xk или step конечное значение в операторе цикла всегда записывать в виде xk + step/2.0;
b)построить цикл не по вещественной переменной x, а по целой I (do I=1,M). Здесь М – количество повторений цикла, рассчитанное вручную при написании программы. При этом в цикле придется пересчитывать целочисленную переменную I в вещественную переменную x оператором х=xn+step*(I-1). В этом случае ошибка вычислений не накапливается;
c)выражать угол alpha в целых градусах, а не в радианах, и при этом использовать функции sind, cosd;
d)координаты последней точки участка вывести после цикла.
Пример
Функция задана графически на интервале [-2, 3]
Уравнения участков графика
№ |
Границы |
Уравне- |
Шаг |
Количество |
Примечание |
|
участка |
ние |
цикла |
точек |
|||
|
|
|
|
|
|
|
|
|
y =x/2 +1 |
|
|
Прямая пересекает оси в точках |
|
1 |
[-2, 0] |
1 |
3 |
(-2,0) и (0,1). Уравнение прямой |
||
|
|
|
|
|
в отрезках. |
|
|
|
|
|
|
|
|
|
[0, 1] |
x = cos α |
|
|
Параметрические уравнения ок- |
|
2 |
3 |
31 |
ружности радиуса R=1 с центром |
|||
α [0, 90▫] |
y = sin α |
|||||
|
|
|
|
|
в начале координат. |
|
3 |
[1, 3] |
y = -1 |
нет |
2 |
Горизонтальная прямая (парал- |
|
лельна оси Х) |
||||||
|
|
|
|
|
Практикум по современному Фортрану
25
Программа
Program Function_graph ! Табуляция функции
!студент (фамилия, имя) группа № работа № вариант №
Implicit None
Real x, y, alpha
Integer,parameter :: tabl=6 ! имени tabl присвоен номер устройства 6 Integer k ! номер точки криволинейного участка
! участки для AGrapher
Open(1,File=’L3_F1.txt’)! 1 – координаты точек прямой
Open(2,File=’L3_F2.txt’)! 2 – координаты точек дуги окружности Open(3,File=’L3_F3.txt’)! 3 – горизонталь (координаты граничных точек) Open(tabl,File=’Out.txt’)! контрольный текстовый файл
Write(tabl,*)’прямая’ Do x= -2, 0, 1
y = 0.5*x+1
Write(1,*)x,y; Write(tabl,*)’(x,y)=’,x,y
Enddo
Write(tabl,*)’дуга окружности’
k=0 ! начальная установка счетчика точек на дуге окружности
Do alpha=0,90,3 ! аргумент функций Sind, Cosd - в градусах, шаг цикла - целый x=Cosd(alpha)
y=Sind(alpha) Write(2,*)x,y k=k+1
! в tabl печатается каждая 5-я точка, Mod(k,5) – остаток от деления k на 5 if(Mod(k,5)==1) Write(tabl,*)’(x,y)=’, x,y
Enddo
Write(tabl,*)’Горизонталь - две точки без цикла’
Write(tabl,*) ’(1,-1) ==> (3,-1,)’ Write(3,*) 1,-1; Write(3,*) 3,-1
End Program Function_graph
Контрольные вопросы к защите работы
1.Что такое цикл?
2.Назовите три вида циклов.
3.Приведите блок-схему и пример бесконечного цикла.
4.Приведите блок-схему и пример итеративного цикла.
5.Приведите блок-схему и пример цикла по переменной.
6.Объясните формулу для числа повторений цикла по переменной.
7.Приведите подробную блок-схему цикла по переменной.
8.Как предотвратить возможную потерю последнего выполнения тела цикла по вещественной переменной? Варианты решения с объяснениями.
Практикум по современному Фортрану
26
9.Подсчитайте количество повторений циклов:
a)do alpha=0,90,2 ;
b)do alpha=90,0,2 ;
c)do alpha=90,0,-2 ;
d)do alpha=0,9 ;
e)do alpha=9,0 ;
f)do alpha=1.57, 3.14, 0.3 .
10.Поясните на блок-схемах роль оператора Enddo в каждом из трех видов циклов.
11.Поясните на блок-схемах роль оператора Exit в каждом из трех видов циклов.
12.Поясните на блок-схемах роль оператора Сycle в каждом из трех видов циклов.
Пример контрольного задания
1. Рассчитайте количество повторений цикла do x=3.15, 2.12, 1.3
2.Напишите оператор цикла по переменной для вывода на экран значений x и tg x, если x изменяется от –100о до –200о, шаг выберите сами. Приведите блок-схему этого оператора.
3.Для фрагмента программы
x = 0.0
Do k = 2, 8, 2 x = x + 0.8
if (x<2 .or. x>3) then y = x*2 + 1.0/k
else exit
endif
write(1, *) x, y
enddo ! выполните следующее:
a)приведите блок-схему;
b)опишите типы всех переменных;
c)напишите, какие и сколько значений x и y будут выведены на устройство 1 в результате работы цикла.
4.Напишите оператор цикла Do while для вывода на экран значений x и y = sin2x + cos2x, если x изменяется от –π/4 до 1,5π с шагом π/10. Приведите блок-схему этого оператора.
Практикум по современному Фортрану

27
Варианты индивидуальных заданий
№ |
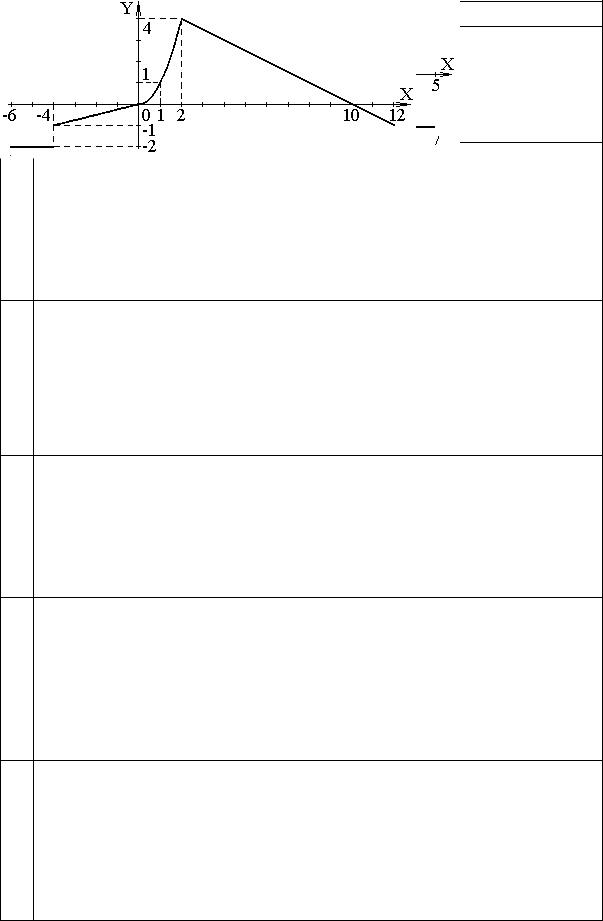
Графики |
1
2
3
4
5
Практикум по современному Фортрану
28
№ |
Графики |
6
7
8
9
10
11
Практикум по современному Фортрану

29
№ |
Графики |
12
13
14
15
16
17
Практикум по современному Фортрану

30
№ |
Графики |
18
19
20
21
22
23
Практикум по современному Фортрану

31
№ |
Графики |
24
25
26
27
28
29
Практикум по современному Фортрану
