
учебное пособие по лр_фортран
.pdf
32
№ |
Графики |
30
1.4. Попадание точки в заданную область плоскости Задание
1.Область заштрихована и ограничена линиями контура.
2.Определить графики линий контура:
a)для каждой i-ой линии контура задать область определения и уравнение y = fi(x) – проверить уравнения в Agrapher;
b)написать программу табулирования fi(x), полученные таблицы импортировать в Agrapher, настроив линии – красным цветом, точки удалить – график должен повторять рисунок индивидуального задания;
c)сохранить график в файле area.agr (этот график используется в дальнейшем).
3.Описать математически систему неравенств, обеспечивающую попадание произвольной точки в заштрихованную область – проверить правильность системы неравенств в AGrapher.
4.Рисунок индивидуального задания накрыть прямоугольной сеткой,
вузлах которой находятся точки для проверки системы неравенств:
a)прямоугольник должен на 10-20% перекрывать заданный контур с каждой из четырех сторон;
b)рекомендуемое число узлов сетки – 20-40 по каждой оси. Определить параметры сетки: начальное и конечное значения x и y, шаг изменения x и y.
5.Дополнить программу из пункта 2:
a)сгенерировать узлы сетки, используя ее параметры;
b)проверить соответствие координат каждой точки сетки системе неравенств, используя для этого единственный оператор IF;
c)записать координаты точки (x, y) в один из двух файлов:
если точка в пределах заштрихованной области – в файл in.txt, если точка за пределами заштрихованной области – в файл out.txt.
6.Дополнить график в Agrapher:
a)прочитать график контурных линий из файла area.agr ;
b)импортировать таблицы из файлов in.txt и out.txt ;
c)установить для точек из in.txt и out.txt разные цвета и удалить линии, соединяющие точки;
Практикум по современному Фортрану

33
d) предъявить преподавателю результат на экране.
Содержание отчета
1.Название работы, номер варианта индивидуального задания.
2.Фамилия, имя, отчество и номер группы студента.
3.Рисунок в том виде, как он приведен в варианте задания.
4.Уравнения всех линий, ограничивающих заштрихованную область.
5.Система неравенств координат всех точек заштрихованной области.
6.Блок – схема и распечатка текста программы.
При подготовке к защите ответить на контрольные вопросы.
Комментарии к заданию
1.В системе неравенств показать объединение квадратной скобкой, пересечение – фигурной скобкой.
2.Таблицу основных уравнений смотрите в разделе 7.3.
3.При составлении системы неравенств рекомендуется рассматривать область по отдельным фрагментам, что поможет в решении задачи. Система неравенств в этом случае представляется объединением групп неравенств, соответствующих этим фрагментам.
4.Рекомендуется воспользоваться симметрией заданной области, иногда это помогает уменьшить количество неравенств.
5.Генерируя точки – узлы сетки, воспользуйтесь вложенными циклами для задания координат x,y для точек.
Пример
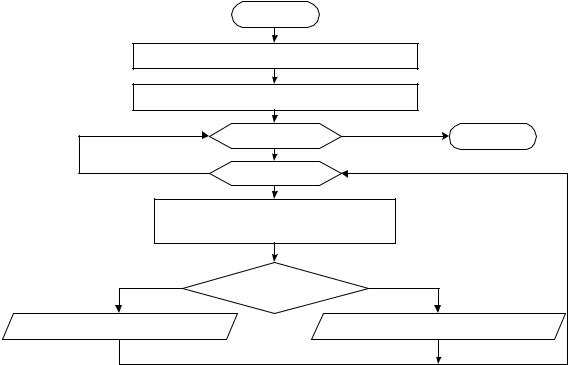
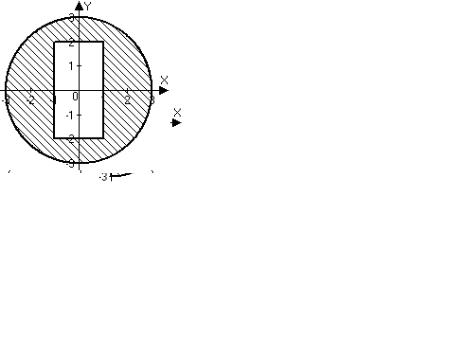
На рисунке показана заштрихованная область и ограничивающий ее пунктирный прямоугольник. Точка находится в пределах заданной области, если она принадлежит хотя бы одному из двух фрагментов В или A, причем из-за |x|<3 вертикальные стороны прямоугольника A -пунктирные.
|
|
|
|
|
|
Система неравенств: |
|||
y ≥2 |
|
|
|
||||||
|
|
|
|
|
|
|
(фрагмент A) |
||
у ≤4 |
|
|
|||||||
|
|
x |
|
<3 |
|
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
2 |
+ y |
2 |
|
(фрагмент B) |
||||
x |
|
|
|
|
≤9 |
||||
x |
≤0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
Границы прямоугольника, содержащего область: –4 ≤ x ≤ 4; –4 ≤ y ≤ 5 В качестве шага изменения x и y выбрано 0.4 .
Практикум по современному Фортрану
|
|
34 |
|
|
Блок-схема программы. |
|
|
|
|
|
|
Начало |
|
|
Табуляция линий - границ области |
|
|||
|
Открытие файлов In.txt иOut.txt |
|
||
|
|
x = -4, 4, 0.4 |
Конеццикла |
Конец |
|
|
|
||
Конеццикла |
y = -4, 4, 0.4 |
|
|
|
|
|
|
|
|
|
A = (y >= 2) и(y <= 4) и(|x| < 3) |
|
||
|
B = (x + y <= 9) и(x <=0) |
|
|
|
да |
|
А или В |
нет |
|
|
|
|
|
|
x, y => вфайл«In.txt» |
|
x, y => вфайл«Out.txt» |
||
Программа.
Program Region ! Попадание точки в область плоскости ! студент (фамилия, имя) группа № работа № вариант №
Implicit none Real x, y
Integer, parameter:: inside=1, outside=2 ! Номера устройств
Logical A, B
Open(inside, file=’in.txt’) ! координаты точек внутри области
Open(outside, file=’out.txt’)! координаты точек вне области
Open(3, file=’3.txt’) ! прямоугольник, ограничивающий фрагмент A
Open(4, file=’4.txt’) ! прямоугольник, ограничивающий фрагмент В ! Табуляция линий – границ области (файлы на устройствах 3 и 4)
. . .
! цикл по Y внутри цикла по X - перебор точек сетки
Do X = -4, 4, 0.4
Do Y = -4, 5, 0.4 |
|
|
A = |
y>=2 .and. y<=4 .and. abs(x)<3 ! фрагмент A |
|
В = |
x*x + y*y <= 9 .and. x<=0 |
! фрагмент B |
If (A .or. B) then |
|
|
Write(inside, *) x, y |
|
|
Else |
|
|
Write(outside, *) x, y |
|
|
End |
If |
|
End Do |
|
|
End Do |
|
|
End Program Region
Практикум по современному Фортрану
35
Контрольные вопросы к защите работы
1.Как в логическом выражении распределяются приоритеты между операциями отношения, числовыми, логическими?
2.Пять логических операций (три основные и две дополнительные) с таблицами истинности и примерами.
3.Приоритеты логических операций в логическом выражении.
4.Шесть операций отношения с примерами.
5.Запись на Фортране логических констант.
6.Что называется циклом? Его стандартная блок-схема в программе.
7.Объясните формулу числа повторений цикла по переменной.
8.В каких случаях целая переменная цикла лучше вещественной?
9.Как по-другому можно назвать цикл по переменной? Приведите пример.
10.Приведите блок-схему и пример вложенных циклов.
11.Приведите блок-схему, пример одноблочного условного оператора.
12.Приведите блок-схему, пример двухблочного условного оператора.
13.Приведите блок-схему и пример условного оператора без блоков.
Пример контрольного задания
1. Напишите условный оператор для вычисления значения переменной.
|
|
2 |
x |
3 |
|
|
при |
х < |
2 , |
|
|
|
|
|
|
|
|||||
|
9 |
|
|
|
||||||
|
|
|
2 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Y = |
sec |
|
|
|
при |
2 |
≤ |
х < 4 , |
||
|
|
x |
||||||||
|
|
|
|
x |
|
|
х |
≥ |
4 |
|
|
3 e |
+ 2 при |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Подсчитайте количество выведенных строк
Do a = 22, 9, -8 Do b = 3, 19, 11
write(*, *) a, b enddo
enddo
Какие значения a и b будут выведены?
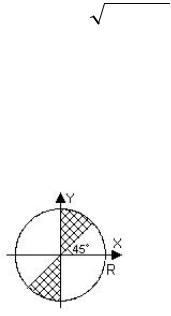
3. |
При каких значениях координат точка [x, y] |
|
|
находится в заштрихованной области |
|
|
плоскости? Опишите эти условия: |
|
|
a) |
в виде системы неравенств; |
|
b) |
в виде логического выражения |
|
(без промежуточных переменных). |
|
Практикум по современному Фортрану
36
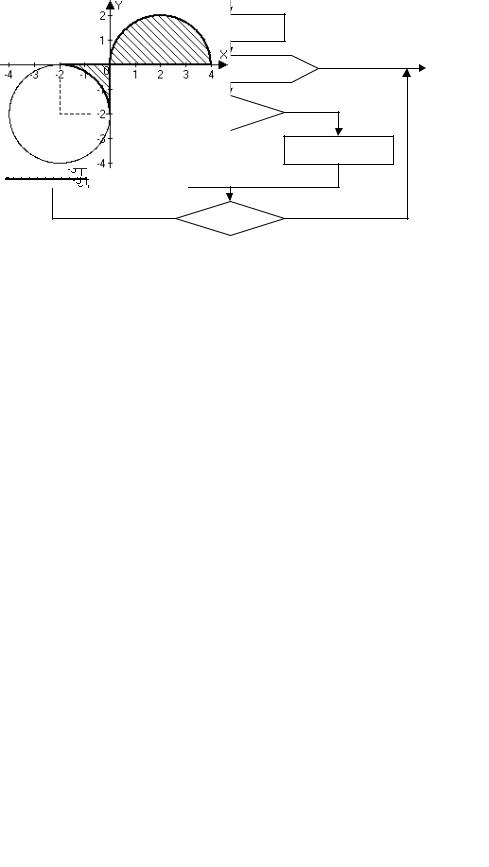
4. Напишите по блок-схеме фрагмент программы на Фортране.
|
a = 0 |
|
|
x = 2, 3, 0.2 |
Конец цикла |
|
|
|
|
x < 2.5 |
|
a = a + 2x |
|
a = a + x |
нет |
a > 10 |
да |
|
|
Варианты индивидуальных заданий
№ |
Рисунки |
№ |
Рисунки |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
3 |
|
4 |
|
|
|
|
|
5 |
|
6 |
|
|
|
|
|
Практикум по современному Фортрану

|
|
37 |
|
|
|
|
|
№ |
Рисунки |
№ |
Рисунки |
|
|
|
|
7 |
|
8 |
|
|
|
|
|
9 |
|
10 |
|
|
|
|
|
11 |
|
12 |
|
|
|
|
|
13 |
|
14 |
|
|
|
|
|
15 |
|
16 |
|
|
|
|
|
Практикум по современному Фортрану

|
|
38 |
|
|
|
|
|
№ |
Рисунки |
№ |
Рисунки |
|
|
|
|
17 |
|
18 |
|
|
|
|
|
19 |
|
20 |
|
|
|
|
|
21 |
|
22 |
|
|
|
|
|
23 |
|
24 |
|
|
|
|
|
25 |
|
26 |
|
|
|
|
|
Практикум по современному Фортрану
|
|
39 |
|
|
|
|
|
№ |
Рисунки |
№ |
Рисунки |
|
|
|
|
27 |
|
28 |
|
|
|
|
|
29 |
|
30 |
|
|
|
|
|
1.5. Приближенное вычисление функции – сумма степенного ряда Задание
1.Составить программу Pro1, которая для рекомендованного в инди-
видуальном варианте значения аргумента x = x0 и заданного значения точности ε:
a)вычисляет значение функции f(x) с помощью встроенной функции Фортрана;
b)вычисляет приближенное значение f(x), суммируя члены ряда Тейлора, и определяет их количество, необходимое для достижения заданной точности ε;
c)формирует три текстовых файла для пакета AGrapher:
−зависимость значения члена ряда an от n;
−зависимость частичной суммы членов ряда Sn от n;
−значение встроенной функции f(x), одно и то же при всех значениях n;
для построения графиков принять ε = 10-4;
d)выводит в текстовый файл Out.txt результаты суммирования с пояснениями:
−значение ε;
−значение аргумента x = x0;
−f(x), вычисленное по стандартной программе;
−значение суммы членов ряда;
Практикум по современному Фортрану
40
−количество членов ряда, составивших его сумму;
−модуль разности f(x) и суммой ряда.
2.С помощью пакета AGrapher построить графики зависимостей по трем текстовым файлам, созданным в программе Pro1.
3.Составить программу Pro2, модифицировав программу Pro1:
a)значение аргумента x функции f(x) изменять от xn до xk с шагом
xиз расчета 10 – 15 значений;
b)исключить формирование текстовых файлов для графиков;
c)результаты вычислений оформить в виде таблицы (каждая строка таблицы соответствует одному значению x и содержит форматированные результаты).
4.Выполнить программу Pro2 дважды с разными значениями ε:
a)со степенью точности, соответствующей визуальному восприятию графиков;
b)со степенью точности, достижимой при использовании вещественных переменных типа Real.
Содержание отчета
1.Название работы, номер варианта индивидуального задания.
2.Фамилия, имя, отчество и номер группы студента.
3.Вариант индивидуального задания (функция, её разложение в ряд Тейлора и область определения аргумента функции).
4.Рекуррентная формула и расчет коэффициента рекурсии с последующей его проверкой для двух членов ряда.
5.Блок-схемы программ Pro1 и Pro2.
6.Распечатки текстов программ Pro1 и Pro2.
7.Распечатка результатов работы программы Pro1.
8.Рисунок или распечатка графиков, построенных в AGrapher по трем файлам, созданным в Pro1.
9.Распечатки двух таблиц с результатами программы Pro2.
При подготовке к защите ответить на контрольные вопросы.
Справочная информация
1.Запись бесконечного ряда Тейлора:
∞
∑an = a0 + a1 + a2 +... + an +..., здесь an – общий член ряда;
n=0
S0, S1,… Sn,… называют частичными суммами бесконечного ряда,
n
S0 = a0 , S1 = a0 + a1, …, Sn = ∑ak = a0 + a1 + a2 +... + an , …
k =0
Практикум по современному Фортрану
41
2.Сходящимся называется ряд, у которого последовательность частичных сумм имеет конечный предел S, т.е. limn→∞ Sn = S , иначе ряд называется расходящимся. S называется суммой сходящегося ряда.
Нахождение этой суммы является целью лабораторной работы.
3.Величина n! называется “n-факториал” и вычисляется по формуле
|
n |
n! = 1 2 3 … (n – 1) n = (n – 1)! n |
или n! = ∏k |
при 0! = 1. |
k =1 |
|
Комментарии к заданию
1.Обратите внимание на то, что в Вашем индивидуальном задании:
a)нумерация членов ряда может начинаться не с «0», а с «1» (n=1);
b)a0 может быть функцией от x или константой;
c)сумме может предшествовать слагаемое или сомножитель.
2.При суммировании ряда необходимо решить следующие задачи:
a)упростить вычисления - свести их к простейшим операциям;
b)уменьшить число этих операций и время расчета;
c)уменьшить погрешность вычислений.
Эти задачи решает рекуррентная формула, позволяющая вычислить значение очередного члена ряда, используя уже найденное значение предыдущего. Рекуррентная формула имеет вид:
an+1 = an Tn, где Tn – коэффициент рекурсии.
3.Возможно суммирование только конечного количества членов ряда. Для сходящегося ряда limn→∞ an =0 . Следовательно, начиная с некото-
рого n, отношение |an| > ε перестанет выполняться для любого положительного ε. Этим значением n и следует ограничиться при суммировании бесконечного ряда.
4.Во избежание зацикливания программы вследствие ошибок, значение n следует ограничить, для чего в программе предусмотрена переменная Nmax (равная, например, 100). При n > Nmax суммирование прекращается и выдается сообщение с дополнительной инфор-
мацией (в том числе значение an). Аварийное сообщение может появиться, если:
a)значение |an| приближается к ε. Возможно, ряд просто «не успел» сойтись и достаточно увеличить значение Nmax ;
b)значение |an| на порядки превышает ε, то есть ряд не сходится. В этом случае следует проверить:
−находится ли x в области определения аргумента;
−достижима ли задаваемая погрешность вычислений ε при использовании вещественных переменных типа Real ;
Практикум по современному Фортрану
