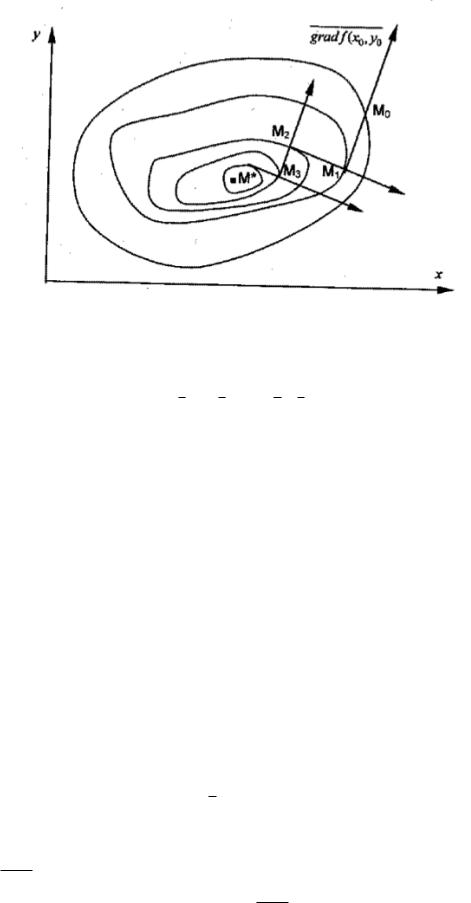
13.3Условие Липшица для градиента ф-и f(x)

Неравенство

jjf0(x) f0(y)jj 6 Rjjx yjj (8)

называется условием Липшица, а R постоянной Липшица.

13.3.1О сходимости градиентого метода

Теорема. Если ф-я f(x) ограничена снизу, ее градиент удовлетворяет условию Липшица (8) и выбор значения k производится методом дробления шага или методом наискорейшего спуска, то какова бы не была начальная точка x0

jjf0(xk)jj ! 0

приk ! 1 (Без док-ва)

xk+1 = xk kf0(xk)

при f0(xk) ! 0 превращается в

xk+1 = xk

13.4Методы покоординатного спуска (для отыскания безусловного экстремума)

Пусть

0x101

Bx2C

x0 = B 0C

@::: A xn0

начальное приближение.

Возьмем @f(x0) и примем

dx1

x1 = x0 o @f(x10) e1

@x

где

24

0 1

1

B0 C

e1 = B:::C @ A

0

e1 единичный вектор-столбец оси x1. .

Следующая итерация состоит в вычислении точки x2 по формуле

x2 = x1 1 @f(x20) e2

@x

где

0 1

0

B1 C

e2 = B:::C @ A

0

единичный вектор оси x2. Дальнейшие итерации аналогичны.

Cледовательно в данном методе спуск происходит по ломанной, состоящей из отрезков прямых, параллельных координатным осям. Спуск по n координатам составляет одну внешнюю итерацию.

Пусть k - номер очередной внешей итерации, а s номер той координаты, по которой производится спуск, тогда рекурентная формула, определяющая следующие приближения к точке минимума будет иметь вид:

xkn+s+1 = xkn+s kn+s @f(xkn+s) esk = 1; 2; ::: s = 1; 2; :::; n (1)

@xs

Или в координатной форме

После s = n счетчик числа больших итераций k увеличивается на единицу, а s = 1. Величина шага k выбирается на каждой итерации или методом дробления шага или методом наискорейшего спуска.

13.4.1Метод покоординатного спуска без вычисления производных

В методе покоординатного спуска в формулах (1) и (2) производные @f(xkn+s) производные можно не

@xs

вычислять, тогда

xkn+s+1 = xkn+s kn+s es k = 1; 2; ::: s = 1; 2; :::; n (3)

При таком определении последующего приближения следует проверить выполнение неравенства

f(xkn+s kn+ses) < f(xkn+s) (4)

Если (4) не выполняется, то следующее приближение xkn+s+1 определяется по формуле

xkn+s+1 = xkn+s + kn+ses (5)

и проверяется выполнение условия

f(xkn+s + kn+ses) < f(xkn+s) (6)

Если одновременно не выполняются неравенства (4) и (6), то производится дробление шага.

13.4.2Рекомендации по применению этого метода

В большинстве методов для определения экстремальных значений ф-ий требуется вычисление первых или даже вторых производных минимизируемых ф-ий, однако в практических задачах нередко встречаются случаи, когда минимизируемая ф-я либо не обладает нужной гладкостью (производные с разрывами, не всегда вычисляются) либо являются гладкой, но вычисление ее производных с требуемой точностью требует слишком большого объема работ. В таких случаях целесообразно использовать методы покоординатного спуска без вычисления производных.

25

Часть III

Минимизация ф-ий многих переменных при ограничениях-равенствах

14 Относительный (условный) экстремум

Пусть необходимо найти экстремумы ф-и f(x) и нужно найти f(x) ! max f(x) ! min при наличии ограничений типа равенства

gi(x) = 0 i = 1; 2; :::; m (1:1)

Условия (1:1) принято называть у-ниями связи.

Определение 1. Точка x удовлетворяющая условиям (1:1) называется допустимой.

Определение 2. Допустимая точка x доставляет относительный или условный локальный минимум ф-и f(x), если можно указать такое число

" > 0

что для всех x, удовлетворяющих у-ниям связи (1:1) и условию

jx x j < "

имеет место неравенство

f(x) > f(x )

т. е. в этой точке имеет место наименьшее значение ф-и.

Определение 3. Допустимая точка x доставляет относительный или условный локальный максимум ф-и f(x), если можно указать такое число

" > 0

что для всех x, удовлетворяющих у-ниям связи (1:1) и условию

jx x j < "

имеет место неравенство

f(x) < f(x ).

Определение 4. Точку x называют глобально-оптимальным решением задачи (1:1) на минимум, если

f(x ) = min f(x)

при

gi(x) = 0 i = 1; 2; :::; m

15Необходимые условия локального экстремума при ограниченияхравенствах

15.1Метод исключения

Пусть даны n функций от n переменных: g1(x1; x2; :::; xn); :::; gn(x1; x2; :::; xn), которые определены в некоторой n-мерной области D и имеют в ней непрерывные частные производные по всем переменным. Определитель

26

называют функциональным определителем Якоби или Якобианом.

Рассмотрим случай, когда у-ния связи (1:1) могут быть разрешены относительно части переменных. Будем предполагат, что ф-и gi(x) i = 1; 2; :::; m имеют в окрестности рассматриваемой допустимой точки x непрерывные частные производные по всем аргументам до второго порядка включительно. Кроме того предполагаем, что ранг матрицы Якоби для этих функций рассматриваемой в точке x равен m. Ненарушая общности предположим так же, что отличен от нуля определитель (Якобиан), составленный из частных производных по первым m аргументам:

Тогда по теореме о неявных функциях в некоторой окрестности точки x система у-ний (1:1) разрешима относительно x1; x2; . . . ; xm т. е. представима в виде

xj = 'j(xm+1; xm+2; :::; xn) j = 1; 2; :::m (1:3)

'j(xm+1; xm+2; :::; xn) непрерывно дифференцируемые в рассматриваемой окрестности ф-и. Переменные xm+1; :::; xn называют независимыми переменными, а x1; :::; xm зависимыми переменными. Подставляя (1:3) в ф-ию f(x) получим задачу определения безусловного экстремума ф-и n m переменных.

f('j(xm+1; xm+2; :::; xn); :::; 'm(xm+1; xm+2; :::; xn); xm+1; :::; xn) = fe(xm+1; :::; xn)

Однако провести исключение части переменных обычно бывает трудно или даже невозможно.

15.2Классическая ф-я Лагранжа. Классический метод множителей Лагранжа

В методе исключения нарушается симметрия в отношении переменных: часть из них трактуются как независимые, а часть как зависимые. Одни переменные исключаются, другие сохраняются. Лагранжем был предложен метод, в котором все переменные сохраняют одинаковую роль (внешне, однако и при выводе и при использовании неявно разделяются).

В точке x , доставляющей безусловный экстремум ф-и, полный дифференциал ф-и равен 0

где dxr дифференциалы зависимых переменных r = 1; 2; :::; m, связанные с дифференциалами независимых переменных dxj j = m + 1; :::; n следующим образом

Исключим теперь дифференциалы зависимых переменных из у-ний (2:1) и (2:2). Для этого умножим каждое из у-ний системы (2:2) на произвольные множители 1; 2; :::; m и результаты сложим с у-нием

(2:1)

Получим следующее равенство

Определим множители 1; 2; :::; m чтобы обратились в нуль коэффициенты при дифференциалах ¾зависимых¿ переменных

Это можно сделать так как определитель (1:2) не равен 0. При выбранных таким образом значениях множителей в равенстве (2:3) останутся только слагаемые, содержащие дифференциалы независимых переменных. Поэтому коэффициенты при этих дифференциалах должны быть равны 0.

Следовательно, получена система n+m у-ний (1:1) (2:4) (2:5) относительно неизвестных x1; :::; xn; 1; :::; mэто и есть метод множителей Лагранжа.

27