6. Непараметрические методы изучения связи.

Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие характеристики могут быть оценены только по номинальной шкале (качественные показатели) или по порядковой шкале. Для установления наличия и тесноты связи в таких случаях используются непараметрические методы изучения связи.

1. Метод ранговой корреляции.

Для оценки тесноты связи между признаками, оцененными при помощи порядковой (ранговой) шкалы используется метод ранговой корреляции. Естественно, что этот метод применим также для признаков, оцененных по интервальной или относительной шкале.

Для оценки тесноты связи используется коэффициент ранговой корреляции, который по смыслу идентичен линейному коэффициенту корреляции.

Чаще всего при использовании этого метода вычисляется ранговый коэффициент Спирмена либо ранговый коэффициент Кендэла. Расчет коэффициента Спирмена основан на фиксации разности рангов двух параллельных рядов наблюдений – ряда признакаи рада признака: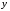

,

где , то есть разность рангов каждой пары значенийи;

- число наблюдений.

Коэффициент корреляции рангов Кендэла определяется по формуле:

, где.

Порядок расчета коэффициента Кендэла следующий:

• значения факторного признака записываются в порядке возрастания, и каждому значению факторного признака ставится в соответствие значение результативного признака;

• значения результативного признака ранжируются;

• для каждого значения результативного признака подсчитывается число следующих за ним рангов более высокого порядка (со знаком "+") и число следующих за ним меньших по значению рангов(со знаком "-").

Если отдельные значения иповторяются, то присваиваемый им ранг рассчитывается как средняя арифметическая из суммы мест, которые они занимают по возрастанию.

Коэффициент Кендэла всегда меньше по значению, чем коэффициент Спирмена и для достаточно больших совокупностей . Чем ближе коэффициенты к единице (по модулю), тем теснее зависимость, а близость к нулю означает отсутствие связи или весьма малую зависимость.

Критическое значение коэффициента Спирмена определяется по таблице в зависимости от уровня значимостии числа наблюдений. Если, то существенность связи доказана с вероятностью.

Кроме того, для случаев, когда можно проверить значимость коэффициентов ранговой корреляции с использованием- критерия:

Коэффициенты ранговой корреляции	Расчетное значение - критерия	Критическое значение - критерия
Пирсона		По распределению Стьюдента для уровня значимости и числа степеней свободы
Кэндела		По нормальному распределению для уровня значимости

Коэффициент корреляции считается значимым на уровне , если расчетное значения критерия превышает критическое.

При ранжировании иногда значения признаков двух или большего числа объектов равны между собой. Такие объекты называются связанными и им приписываются одинаковые средние ранги. Средние ранги равны среднему арифметическому номеров этих объектов в общем списке проранжированных объектов. Дл расчета коэффициента Спирмена в случае наличия связанных рангов существует специальная формула, но приблизительная оценка может быть получена и по общей формуле.