7.1.6. Зависимость оптимальной и максимальной подач от относительного погружения

С увеличением ε величины qmax также увеличиваются по криволинейному закону, а qопт, сначала увеличиваются с ростом ε, а затем при 0,5 < ε < 1 начинают уменьшаться. В частности, при ε = 1 кривая q(V) выходит из начала координат.

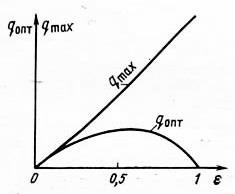
Рис. 7.6. Зависимость оптимальной qопт и максимальной qmax подачи от относительного нагруження ε

Наибольшая величина qопт достигается при ε = 0,5 – 0,6.

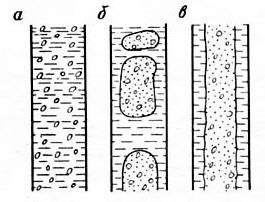
Рис. 7.7. Структуры газожидкостного потока: а - эмульсионная; б - четочная; в - стержневая

7.1.7. Структура потока гжс в вертикальной трубе

Вследствие своей малости (доли мм) и большой плотности газовые пузырьки обладают малой архимедовой силой. Поэтому их скорость всплытия относительно жидкости пренебрежимо мала и в расчетах может не учитываться. Это происходит до тех пор, пока в результате уменьшения давления при движении смеси вверх по трубе газовые пузырьки, расширяясь, увеличивают объемное газосодержание потока до 20 - 25%. Скорость всплытия таких глобул в результате действия архимедовой силы становится большой, достигая нескольких десятков сантиметров в секунду. Это ухудшает энергетические показатели процесса подъема.

7.2. Уравнение баланса давлений

Когда по НКТ движется ГЖС

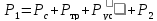, (7.8)

где Р₁ - давление в нижней части трубы, Рс - давление, уравновешивающее гидростатическое давление столба ГЖС, Ртр - потери давления на преодоление сил трения при движении ГЖС, Рус - потери давления на создание ускорения потока ГЖС, так как его скорость при движении в сторону меньших давлений увеличивается из-за расширения газа; Р₂ - противодавление на верхнем конце трубы.

Известно давление вверху Р₂ и требуется определить давление внизу Р₁ или наоборот. Но требуется определить расход поднимаемой жидкости q при заданном перепаде давления Р₁ - Р₂. Или определить необходимое количество газа Го для подъема заданного количества жидкости q при заданном перепаде давления Р₁ – Р_2.

Обозначим ρ - плотность жидкости, L - длина трубы по вертикали, ρс - плотность ГЖС, h - потеря напора на трение на участке трубы длиной в 1 м столба ГЖС, hус - потеря напора на ускорение на участке трубы длиной в 1 м столба ГЖС.

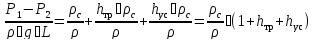. (7.10)

Если для таких коротких участков трубы рассчитать падение давления ΔPi, то общий перепад составит сумму

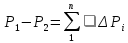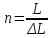. (7.14)

(7.15)

Если известно давление вверху Р₂ , то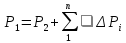, если известно давление внизу P₁, то

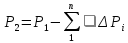. Задача сводится к расчету потерь давления на коротких участках подъемника при заданных параметрах движения (q, d, Г, ρ и пр.) и последующем их суммировании.

7.3. Плотность газожидкостной смеси

Можно представить, что все газовые пузырьки занимают в сечении трубы суммарную площадь fг, а жидкость - остающуюся площадь в том же сечении fж, так что

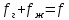, где f - площадь сечения трубы. 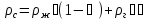, гдеρж и ρг - плотность жидкости и газа при термодинамических условиях сечения, а fг / f обозначают через φ - истинное газосодержание потока. φ = 0,833·βс, а 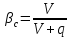- расходное газосодержание потока ГЖС.

8. Эксплуатация фонтанных скважин

Условие фонтанирования:

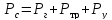, (8.1)

где Р_с - давление на забое скважины; Р_г, Р_тр, Р_у - гидростатическое давление столба жидкости в скважине, рассчитанное по вертикали потери давления на трение в НКТ и противодавление на устье, соответственно.

Различают два вида фонтанирования скважин:

• фонтанирование жидкости, не содержащей пузырьков газа, - артезианское фонтанирование;

• фонтанирование жидкости, содержащей пузырьки газа, облегчающего фонтанирование, - наиболее распространенный способ фонтанирования.

Поскольку присутствие пузырьков свободного газа в жидкости уменьшает плотность последней и, следовательно, гидростатическое давление такого столба жидкости, то давление на забое скважины, необходимое для фонтанирования газированной жидкости, существенно меньше, чем при артезианском фонтанировании.