Вопросы к дифференцированному зачету

1. Линейные операции над векторами.

2. Скалярное произведение векторов.

3. Комплексные числа. Действия над комплексными числами.

4. Тригонометрическая форма комплексного числа.

5. Действия над комплексными числами в тригонометрической форме.

6. Прямая линия на плоскости.

7. Условия перпендикулярности и параллельности двух прямых.

8. Эллипс: определение и вывод канонического уравнения.

9. Гипербола: определение и вывод канонического уравнения.

10. Парабола: определение и вывод канонического уравнения.

11. Прямая и плоскость в пространстве.

12. Системы линейных уравнений.

13. Матрицы и их классификация.

14. Операции над матрицами.

15. Определители и их свойства. Теорема Лапласа.

16. Обратная матрица: определение и алгоритм вычисления.

17. N-мерное линейное векторное пространство.

18. Системы векторов, операции над ними.

19. Ранг матрицы. Теорема о ранге матрицы.

20. Линейные операторы и матрицы.

21. Линейная зависимость векторов.

22. Собственные векторы линейных операторов.

23. Решение системы линейных уравнений с помощью определителей. Формулы Крамера.

24. Решение системы линейных уравнений в матричной форме.

25. Решение системы линейных уравнений методом Гаусса.

26. Теорема Кронекера-Капелли.

Самостоятельная работа студентов Пределы и непрерывность

Вычислить пределы, используя правило Лопиталя:
1.
2.
3.
Вычислить пределы:

Точки разрыва функции

1. Исследовать непрерывность функции в точке х=0:

2. Исследовать непрерывность в точке х=0:

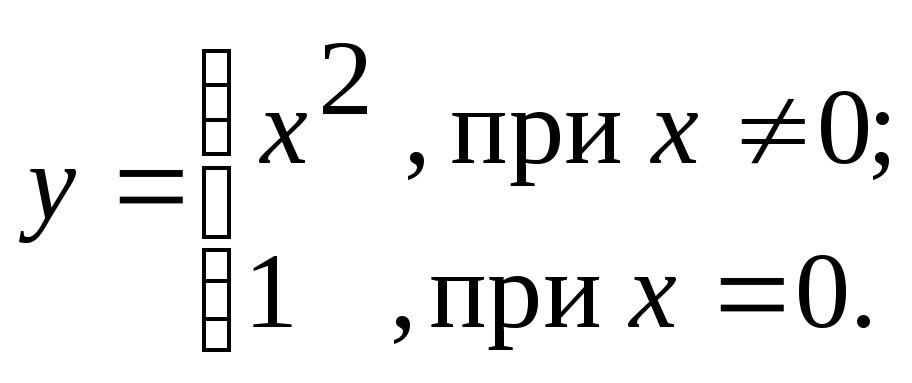
3. Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:

.

4. Исследовать на непрерывность функцию:

5. Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:

y= (cos5x)/x.

6. Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:

y= (2x+1)/x².

7. Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:

8. Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:

9. Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:

10. Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:

Найти асимптоты графиков функций:

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Дифференциальное исчисление

1. Найти производную сложной функции:

1.	6.
2.	7.
3.	8.y= cos( x3+lnx).
4.	9. y= (sinx +5)3.
5.	10. y=ln(x2+2x).

2. Найти производную функции в точке х=1:

.

3. Объем продукции u, произведенный бригадой рабочих, может быть записан уравнением, гдеt– рабочее время в часах. Вычислить производительность труда за час до его окончания.

4. Найти экстремум функции:

1.

2.

3.

4.

5.

6.

5.Определить интервалы возрастания и убывания функции:

1) ;

2) ;

3)

4)

5)

6)

6. Найти точку перегиба функции:

1)

2)

3)

4)

7. Исследовать функции и построить их графики: