1.4 Основные результаты.

XA, кН	XB, кН	XC, кН	YA, кН	YB, кН	YC, кН
-13,3	12	-12	-2,7	7,5	-7,5

2.Кинематический анализ плоского механизма.

2.1 Теоретическая часть.

Исследование кинематических характеристик механизма, совершающего плоскопараллельное движение.

Способы задания движения точки.

Прежде чем заняться исследованием движения точки, определением характеристик этого движения, надо научиться определять положение точки в пространстве в нужный момент времени.

Для этого существует несколько способов задания движения.

1) Естественный способ.

Чтобы определить движение точки естественным способом должно быть заранее задано: траектория движения точки (линия, по которой точка движется); начало отсчёта (точка , от которой по траектории отсчитыва­ется расстояниеs до движущейся точки М) ; направление, в котором от­кладываются положительные значения характеристик движения (указыва­ется стрелкой, либо знаками плюс и минус ); закон движения s = s(t). (2.1)

2) Координатный способ.

Этим способом положение точки, в какой либо системе координат определяется её координатами 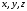. При движении точки эти координаты изменяются. Поэтому, чтобы определить положение точки в нужный момент времени, должны быть заданы координаты как функции

времени 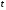: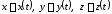(2.2)

Эти функции называются уравнениями движения точки.

Уравнения движения позволяют определить не только положение точки в любой момент времени, но и все характеристики движения, в том числе и траекторию движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .

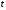3) Векторный способ.

Положение точки можно определить заданием вектора 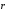, проведённого из неподвижной точки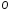, предполагая, что точка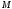 находится на конце этого вектора. Этот вектор называется радиус-вектором точки 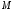. Конечно, чтобы определить положение точки в любой момент времени, радиус-вектор должен быть задан как функция времени 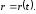(2.3)

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор 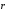на составляющие по осям координат:

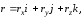где 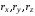- проекции вектора на оси;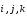– единичные векторы, направленные по осям, орты осей. Так как начало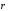вектора находится в начале координат, то проекции вектора будут равны координатам точки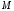.Поэтому

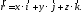(2.4)

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

 φ=φ(t) – уравнение вращательного движения твердого тела. (2.5)

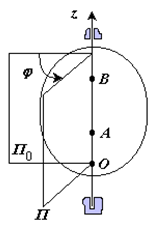рис. 2.1

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

. (2.6)

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту.  За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин).  Разделив этот угол на число секунд в минуте, получим

. (2.7)

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

. (2.8)

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

. (2.9)

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

. (2.10)

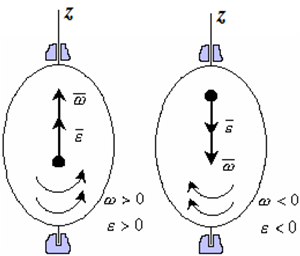
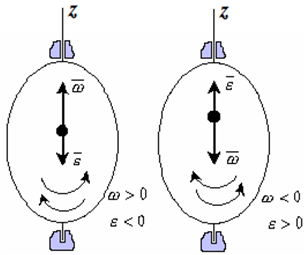
рис. 2.2

Если ε >0 и ω >0 (рисунок 2.2), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону.  Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.

При ε <0 и ω <0 – тело вращается ускоренно  в отрицательную сторону.  Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .

Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.

Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.

Определение: Вектором угловой скорости называется вектор модуль, которого равен величине угловой скорости тела направленный по оси вращения в сторону чтобы, смотря навстречу этому вектору можно было видеть вращение тела происходящем в направлении против хода часовой стрелки.

Определение: Вектором углового ускорения тела называется вектор равный первой производной по времени от вектора угловой скорости. Он также направлен по оси вращения тела. Если эти величины 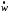,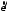имеют одинаковые знаки, то вращение тела ускоренно. Векторы направлены одинаково. А если знаки разные вращение замедленно и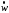,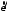векторы направлены противоположно.

Скорости и ускорения точек вращающегося твердого тела.

Так как траектории точек вращающегося тела – окружности, при определении скорости и ускорения удобно воспользоваться естественным способом задания движения (рисунок 2.3). Дуговая координата, определяющая положение точки на траектории, связана с углом поворота равенством:

s = φR . Отсюда:

. (2.11)

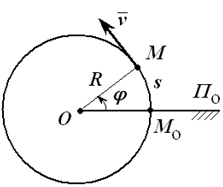рис. 2.3

Скорость ν = ν_ττ еще называют линейной или окружной скоростью. Она направлена по касательной к траектории движения точки.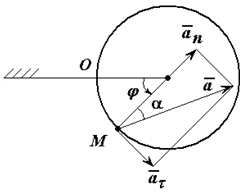

рис. 2.4

Ускорение (рисунок 2.4) определяется как сумма касательного и нормального ускорений:

. (2.12)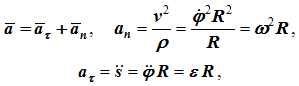

. (2.13)

модуль ускорения

. (2.14)

Угол α, образованный вектором ускорения точки с радиусом окружности OM, для всех точек тела в любой момент времени одинаков,

. (2.15)

Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным:

. (2.16)

Плоскопараллельное движение твердого тела.

Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П . Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в

кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.

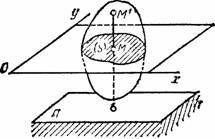
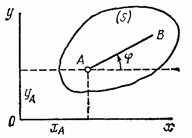
Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П. При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.

Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.

Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 28). В свою очередь положение отрезка АВ можно определить, зная координаты и точки А и угол , который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.

При движении фигуры величины 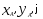будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости.

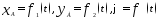
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.

Первые два из уравнений движения определяют то движение, которое фигура совершала бы при 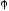= const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А.

Третье уравнение определяет движение, которое фигура совершала бы при и , т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.

Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса, а также угловая скорость и угловое ускорение вращательного движения вокруг полюса. . Абсолютная скорость любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости про-извольно выбранного полюса в поступательном движении плоской фигуры и вращательной скорости во вращательном движении фигуры относительно полюса.