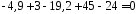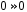- •Содержание
- •1.Определение реакций опор составной конструкции.
- •1.1 Теоретическая часть.
- •Момент силы относительно точки и оси
- •1.2 Постановка задачи.
- •1.3 Алгоритм решения задачи.
- •1.4 Основные результаты.
- •2.Кинематический анализ плоского механизма.
- •2.1 Теоретическая часть.
- •Способы задания движения точки.
- •Определение скоростей точек в плоскопараллельном движении
- •2. Определение ускорений точек.
- •2.4 Основные результаты.
Момент силы относительно точки и оси
Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.
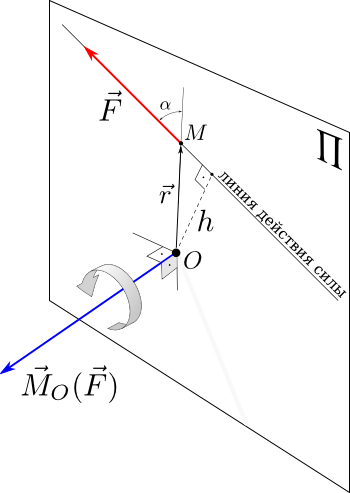
рис.1.2
Если известен
радиус-вектор
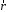 точки
приложения силы
точки
приложения силы 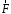 относительно
точки О, то момент этой силы относительно
О выражается следующим образом:
относительно
точки О, то момент этой силы относительно
О выражается следующим образом:
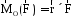 .
(1.8)
.
(1.8)
Действительно, модуль этого векторного произведения:
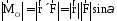 .
(1.9)
.
(1.9)
В соответствии
с рисунком  ,
поэтому:
,
поэтому:
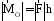 |.
(1.10)
|.
(1.10)
Вектор 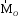 ,
как и результат векторного произведения,
перпендикулярен векторам
,
как и результат векторного произведения,
перпендикулярен векторам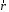 и
и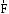 ,
которые принадлежат плоскости Π.
Направление вектора
,
которые принадлежат плоскости Π.
Направление вектора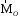 таково,
что глядя по направлению этого вектора,
кратчайшее вращение от
таково,
что глядя по направлению этого вектора,
кратчайшее вращение от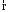 к
к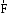 происходит по часовой стрелке. Другими
словами, вектор
происходит по часовой стрелке. Другими
словами, вектор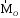 достраивает
систему векторов (
достраивает
систему векторов (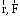 ) до
правой тройки.
) до
правой тройки.
Зная координаты точки приложения силы в системе координат, начало которой совпадает с точкой О, и проекцию силы на эти оси координат, момент силы может быть определен следующим образом:
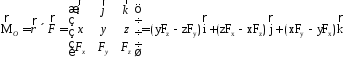 .
(1.11)
.
(1.11)
Момент силы относительно оси
Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку, называется моментом силы относительно оси.
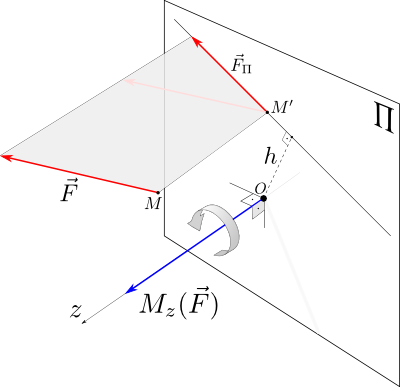 рис.1.3
рис.1.3
Момент силы
относительно оси вычисляется как момент
проекции силы 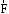 на плоскость Π, перпендикулярную
оси, относительно точки пересечения
оси с плоскостью Π:
на плоскость Π, перпендикулярную
оси, относительно точки пересечения
оси с плоскостью Π:
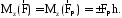 (1.12)
(1.12)
Знак момента определяется направлением вращения, которое стремится придать телу сила F⃗ Π. Если, глядя по направлению оси Oz сила вращает тело по часовой стрелке, то момент берется со знаком ``плюс'', иначе - ``минус''.
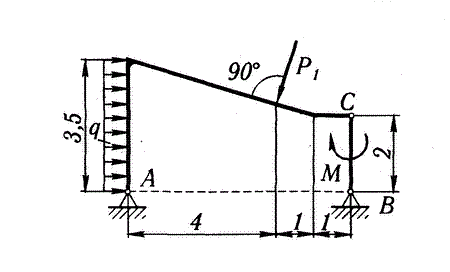
1.2 Постановка задачи.
Определение реакций опор и шарнира С.
|
P1, кН |
M, кН*м |
q, кН/м |
|
5,0 |
24,0 |
0,8 |
1.3 Алгоритм решения задачи.
Разделим конструкцию на части и рассмотрим равновесие каждой из конструкции.
Рассмотрим равновесие всей конструкции в целом. (рис.1.1)
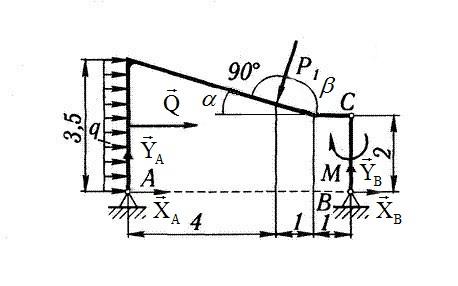
рис. 1.1
Составим 3 уравнения равновесия для всей конструкции в целом:
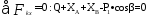
(1)
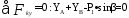
(2)
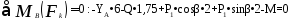 (3)
(3)
Рассмотрим равновесие правой части конструкции.(рис 1.2)
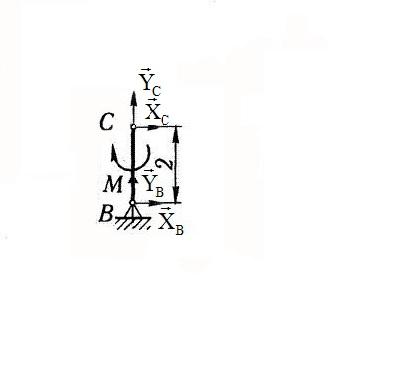
рис.1.2
Составим 3 уравнения равновесия для правой части конструкции:
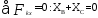 (4)
(4)
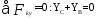 (5)
(5)
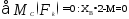 (6)
(6)
Из уравнения 3 находим YA
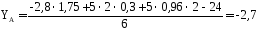 кН
кН
Найдем Q:
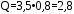 кН/м
кН/м
Найдем угол β:
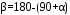
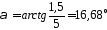
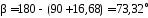
Из уравнения 2 находим YB
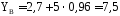 кН
кН
Из уравнения 6 находим XB
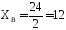 кН
кН
Из уравнения 5 находим YC
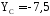 кН
кН
Из уравнения 4 находим XC
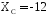 кН
кН
Из уравнения 1 находим XA
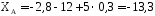 кН
кН
Составим уравнение проверки: