
Электронное пособие по дискретной математике
.pdfМинистерство сельского хозяйства российской федерации
Федеральное государственное образовательное учреждение Высшего профессионального образования (ФГОУ ВПО)
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Факультет прикладной информатики
Кафедра компьютерных технологий и систем
Электронный практикум по дискретной математике
для студентов факультета «Прикладная информатика» по областям

2
Глава 1. Элементы логики предикатов
1.1. Понятие предиката
Предикатом арности n (n-арным, или n-местным предикатом) называют функцию от n переменных Q(x1, x2, … ,xn), определенную на декартовом произведении множеств: X1 X2 … Xn и принимающую значения из множества {И, Л}.
Примеры выполнения заданий
1. Постройте матрицу одноместного предиката Р(x), если:
P(x) = "x кратно 2", где x [1, 14)
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
P(x) |
Л |
И |
Л |
И |
Л |
И |
Л |
И |
Л |
И |
Л |
И |
Л |
2. Изобразите геометрически множество истинности двуместного |
|
||||||||||
предиката P(x,y) = 1/4x 1/4y”, если x, y (-2, 5]; |
|
|
|
|
|
|
|
|
|||
Построим график прямой: |
|
|
Y |
|
|||||||
|
1/4y =1/4x; y = x; |
|
|
|
|
|
|
|
|
||
|
x |
y |
|
|
|
5 |
|
|
|
||
|
0 |
0 |
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
|
|
|
0 |
|
|
|
||
|
|
|
|||||||||
Проверим точку выше графика прямой |
|
|
|
|
|
|
|
5 |
|||
|
|
|
|
|
|
|
|||||
-2 |
|
|
|
|
|
||||||
например, с координатами (-1; 2). |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Подставим координаты в неравенство: |
-2 |
|
|
|
|||||||
1/4 (-1) 1/4(2) – это ложно, поэтому область истинности предиката расположена ниже прямой, включая ее точки (т.к. нестрогое неравенство).
Задания для самостоятельного выполнения
1.1.1.Постройте матрицу одноместного предиката Q(x), если:
0)Q (x)=”2x2 |
кратно 5”, x (-8, 13); |
1) |
Q (x)=”3x2 |
кратно 2”, x [-5, 13); |
2)Q (x)=”4x2 |
кратно 5”, x (-10, 11); |
3) |
Q (x)=”3x3 |
кратно 2”, x [-9, 10); |
4)Q (x)=”5x2 кратно 3”, x (-5, 13]; |
5) |
Q (x)=”3x3 |
кратно 4”,x (-7, 12); |
|
6)Q (x)=”5x3 |
кратно 4”, x [-6, 14]; |
7) |
Q (x)=”x4 кратно 2”, x (-11, 1]; |
|
8)Q (x)=”x3 кратно 5”, x (-9, 10); |
9) |
Q (x)=”x2 кратно 3”, x [-7, 12); |
||
x
Q(x)

3
1.1.2. Изобразите геометрически множество истинности одноместных предикатов G(x) и P(x), если:
0) G(x) = ”8 -2x > 4/3”; |
P(x) = ”2 >1/5x -5”; |
|||
1) G(x) = ”-9 < -3x 3/2”; |
P(x) = ”12 > 3/4x > -3”; |
|||
2) |
G(x) = ”0 1/3x >-5/9”; |
P(x) = ”–14 -7x 1/4”; |
||
3) |
G(x) = ”1/4 |
< -3x |
9”; |
P(x) = ”1 1/6x > -1/2”; |
4) |
G(x) = ”1/3 > -6x |
>-6”; |
P(x) = ”5 1/2x -1/4”; |
|
5) G(x) = ”8 -2x > 4/3”; |
P(x) = ”1/10 >1/5x > -5”; |
|||
6) |
G(x) = ”-1 < -3x 3/2”; |
P(x) = ”6 > 1/4x > -3”; |
||
7) |
G(x) = ”0 1/2x >-3/4”; |
P(x) = ”–1 -7x 1/2”; |
||
8) |
G(x) = ”1/5 |
< -3x |
9”; |
P(x) = ”1 1/6x > -1/2”; |
9) |
G(x) = ”1/8 |
> -4x>-8”; |
P(x) = ”2 1/2x -1/4”; |
|
X
0
X
0
1.1.3. Изобразите геометрически множество истинности предиката P(x), решив систему неравенств:
|
|
+ ≤ + |
|
− ≤ − |
|||||||||||||||||||||||
0) P( x)={ |
2x−2 |
≤ |
+ |
|
1) P( x)={ |
|
|
|
|
x |
|
≥ |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
−2 |
− |
||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− > 3 − |
||||||||||||
P(x)={ |
+ ≤ − |
3) P(x)={ + < 8 + |
|||||||||||||||||||||||||
|
− + ≥ − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
P( |
|
|
− |
< |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( − ) + > 0 |
5) P( x)={ |
|
|
|
|||||||||||||||||||||||
|
|
− |
x−1 |
< 0 |
|||||||||||||||||||||||
x)={ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
− |
|
|
< 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
− |
+ |
< 2 |
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
6) P( x)={3−x |
|
|
|
|
( + ) < 5( + ) + ( + ) |
||||||||||||||||||||||
− x < 3 |
P(x)={ |
||||||||||||||||||||||||||
|
|
2 |
|
|
|
( − ) < 7 − ( + ) |
|||||||||||||||||||||
8) P(x)={ − < 1 − |
9) P(x)={( − ) − ( + ) > 0 |
+ > 2 + 6 |
− ( − ) > 2 |

4
X
0
1.1.4. Постройте матрицу двуместного предиката P(x,y) и проверьте решение геометрически:
0)P(x,y)=”3x>-1/2y”, при x, y (-4,4); 2)P(x,y)=”-1/4x 2y”, при x, y [-1,5]; 4)P(x,y)=”5x>1/2y”, при x, y [-6,1); 6)P(x,y)=”-1/10x 5y”, при x,y (-1,7) 8)P(x, y)=”-3x<2y”, при x, y [-5,2);
x y
1)P(x, y)=”1/3x > 9y”, при x, y (-2,5]; 3)P(x,y)=”10x 1/2y”, при x,y (-4,3); 5)P(x,y)=”-4x 2/3y”, при x, y [-5,1]; 7)P(x,y)=”3x 5/3y”, при x, y [-2,4]; 9)P(x,y)=”1/6x>-12y”, при x,y [-1,6).
Y
X
1.1.5. Изобразите геометрически множество истинности двуместного предиката A(x, y).
0) |
A(x, y)=”1/3x > 9y”, |
1) |
A(x, y)=”3x > -1/2y”, |
|
если x, y (-2, 13]; |
|
если x, y (-5, 11); |
2) |
A(x, y)=”-1/4x 2y”, |
3) |
A(x, y)=”10x 1/2y”, |
|
если x, y [-4, 9]; |
|
если x, y (-10, 5); |
4) |
A(x, y)=”5x > 1/2y”, |
|
Y |
|
если x, y [-12, 3); |
|
|
5)A(x, y)=”- 1/10x 5y”,
если x, y (-1, 15);
6)A(x, y)=”3x 5/3y”,
если x, y [-9, 4]; |
X |
|
7) A(x, y)=”-3x < 2y”, |
||
|
||
если x, y [-10, 5); |
|
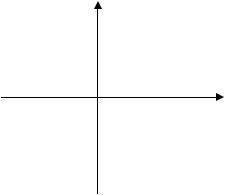
5
8) A(x, y)=”1/6x >- 12y”,
если x, y [-1, 14); 9) A(x, y)=” -4x 2/3y”,
если x, y [-8, 6];
1.1.6. Изобразите геометрически множество истинности двуместного предиката Q(x,y).
0) Q(x, y)=”1/4x2 <2y”, если x, y (-1,6); Y
1)Q(x, y)=”-4x2<2y”, если x,y (-4, 8];
2)Q(x, y)=”-6x2 3y”,если x, y [-2, 7];
3)Q(x, y)=”-5x2 2y”, если x, y [-3,7);
4)Q(x, y)=”3x2<-2y”, если x, y (-2, 6);
5)Q(x, y)=”- 6x2 >3y”, если x, y (-4, 5]; |
0 |
X |
|
6) |
Q(x, y)=”7x2 -3y”, если x, y [-4, 5]; |
|
|
7) |
Q(x, y)=”-4x >1/ 2y”, если x, y (-7,1) |
|
|
8)Q(x, y)=”6x2>- 5y”, если x, y [-3, 4]; 9)Q(x, y)=” 8x2 1/6y”, если x, y [-3, 8);
1.2. Операции над предикатами и кванторами
Все логические операции логики высказываний справедливы и для предикатов (отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция). Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. В математической логике приписывание квантора к формуле называется связыванием, а переменную, к которой он относится, называют связанной иначе свободной. Например, в предикате x A(x, y) z B(c, z) переменные x и z - связанные, а переменные у и z – свободные.
Чаще всего используют два вида кванторов:
Название |
Прочтение |
Обозначение |
Квантор общности |
«все», «всякий», «каждый», |
|
|
«любой» |
|
Квантор |
«существует», «найдется», |
|
существования |
«хотя бы один» |
|
Пусть задан одноместный предикат P(x) на множестве Х = {a1, a2, a3, a4},
тогда: xP(x)=P(a1)&P(a2)&P(a3)&P(a4); xP(x)=P(a1) P(a2) P(a3) P(a4).
6
Говорят, что у квантора всеобщности конъюнктивная природа, а у квантора существования – дизъюнктивная. Квантор уменьшает число свободных переменных в логическом выражении и превращает трёхместный предикат в двухместный, двухместный — в одноместный, одноместный — в высказывание.
Примеры выполнения заданий
1. Пусть предикат Q(x,y) определен на конечных множествах:
X={a1,a2,a3, a4, a5}, Y={b1, b2, b3, b4, b5, b6} и имеет таблицу истинности:
|
|
|
|
Y |
|
|
X |
b1 |
b2 |
b3 |
b4 |
b5 |
b6 |
a1 |
И |
И |
Л |
Л |
И |
Л |
a2 |
Л |
Л |
Л |
И |
И |
Л |
a3 |
И |
И |
Л |
Л |
И |
И |
a4 |
Л |
И |
Л |
Л |
И |
И |
a5 |
И |
И |
И |
И |
И |
И |
С помощью кванторов общности и существования постройте высказывания и определите их истинность.
Решение. Результат применения кванторов общности и существования по x X:
|
|
|
|
|
Y |
|
|
|
|
|
|
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
|
|
xQ(x,y) |
Л |
Л |
Л |
Л |
|
И |
Л |
|
|
xQ(x,y) |
И |
И |
И |
И |
|
И |
И |
|
|
Результат применения |
|
|
Результат применения |
|||||
квантора общности по y Y: |
|
квантора существования по y Y: |
|||||||
X |
yQ(x,y) |
|
|
a1 |
Л |
a2 |
Л |
a3 |
Л |
a4 |
Л |
a5 |
И |
X |
yQ(x,y) |
|
|
a1 |
И |
a2 |
И |
a3 |
И |
a4 |
И |
a5 |
И |
Применив кванторы общности и существования повторно, получим восемь высказываний (0-арных предикатов), представленных в таблице:
Высказывание |
Значение истинности |
|
7 |
|
|
y x Q(x, y) |
Л |
y x Q(x ,y) |
И |
y x Q(x ,y) |
И |
x y Q(x ,y) |
И |
x y Q(x ,y) |
И |
x y Q(x ,y) |
И |
Задания для самостоятельного выполнения
1.2.1. Пусть предикат P(x, y) определен на множествах: X={a1,a2 a3,a4}, Y={b1,b2,b3,b4,b5,b6,b7,b8} и имеет таблицу истинности. С помощью кванторов постройте высказывания и определите их истинность:
0)
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
И |
Л |
И |
|
Л |
И |
И |
Л |
|
a2 |
Л |
И |
И |
И |
|
Л |
И |
И |
Л |
|
a3 |
И |
И |
Л |
И |
|
Л |
Л |
Л |
Л |
|
a4 |
И |
И |
Л |
И |
|
Л |
Л |
Л |
Л |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
Л |
Л |
И |
|
Л |
И |
И |
Л |
|
a2 |
Л |
Л |
Л |
Л |
|
Л |
Л |
Л |
Л |
|
a3 |
И |
И |
Л |
И |
|
Л |
Л |
Л |
Л |
|
a4 |
Л |
Л |
Л |
И |
|
И |
Л |
И |
Л |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
Л |
И |
Л |
|
И |
Л |
И |
Л |
|
a2 |
Л |
И |
И |
Л |
|
Л |
Л |
Л |
И |
|
a3 |
И |
Л |
Л |
Л |
|
Л |
Л |
Л |
И |
|
a4 |
Л |
И |
Л |
И |
|
И |
Л |
Л |
И |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
И |
Л |
И |
|
И |
Л |
Л |
И |
|
a2 |
Л |
Л |
И |
Л |
|
И |
И |
И |
И |
|
a3 |
И |
Л |
И |
Л |
|
И |
И |
Л |
И |
|
a4 |
И |
И |
Л |
И |
|
Л |
Л |
Л |
И |
8
4)
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
И |
Л |
И |
|
Л |
И |
И |
Л |
|
a2 |
Л |
И |
И |
И |
|
Л |
И |
И |
Л |
|
a3 |
Л |
И |
Л |
И |
|
Л |
Л |
Л |
Л |
|
a4 |
И |
Л |
И |
Л |
|
Л |
Л |
Л |
Л |
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
И |
Л |
И |
|
И |
Л |
Л |
Л |
|
a2 |
Л |
И |
И |
И |
|
И |
Л |
Л |
И |
|
a3 |
И |
И |
Л |
Л |
|
И |
И |
Л |
И |
|
a4 |
И |
Л |
И |
Л |
|
И |
Л |
Л |
Л |
6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
И |
Л |
И |
|
И |
И |
И |
Л |
|
a2 |
Л |
И |
И |
И |
|
И |
И |
И |
Л |
|
a3 |
Л |
Л |
И |
И |
|
И |
Л |
Л |
Л |
|
a4 |
И |
Л |
Л |
И |
|
И |
И |
Л |
Л |
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
Л |
Л |
И |
|
Л |
И |
И |
Л |
|
a2 |
И |
И |
Л |
Л |
|
Л |
И |
И |
Л |
|
a3 |
И |
И |
Л |
И |
|
И |
И |
И |
Л |
|
a4 |
И |
И |
Л |
Л |
|
И |
Л |
Л |
Л |
8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
И |
Л |
И |
|
Л |
И |
Л |
И |
|
a2 |
И |
Л |
Л |
И |
|
И |
Л |
И |
Л |
|
a3 |
Л |
И |
Л |
И |
|
И |
Л |
Л |
И |
|
a4 |
Л |
Л |
И |
И |
|
И |
Л |
Л |
Л |
9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
Л |
Л |
Л |
|
Л |
Л |
Л |
Л |
9
a2 |
И |
И |
И |
И |
Л |
И |
И |
Л |
a3 |
Л |
И |
Л |
И |
И |
И |
И |
И |
a4 |
Л |
Л |
Л |
И |
И |
И |
Л |
И |
Решение:
Y |
|
b1 |
|
b2 |
b3 |
|
b4 |
|
b5 |
b6 |
b7 |
b8 |
||
x P(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x P(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
y P(x, y) |
|
|
|
|
X |
|
y P(x, y) |
|
|
|||
a1 |
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
1.2.2. Предикат R(x,y) определен на множествах: X={a1,a2,a3,a4,a5}, Y={b1,b2,b3,b4,b5,b6,b7,b8} и имеет таблицу истинности. С помощью кванторов постройте высказывания и определите их истинность:
0)
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
Л |
Л |
Л |
|
Л |
И |
И |
И |
|
a2 |
И |
И |
Л |
И |
|
И |
И |
Л |
Л |
|
a3 |
И |
И |
Л |
И |
|
И |
Л |
Л |
Л |
|
a4 |
Л |
Л |
Л |
И |
|
Л |
Л |
Л |
Л |
|
a5 |
Л |
Л |
Л |
Л |
|
Л |
Л |
Л |
Л |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
И |
Л |
И |
|
Л |
И |
И |
Л |
|
a2 |
Л |
Л |
Л |
И |
|
Л |
И |
Л |
Л |
|
a3 |
И |
И |
И |
И |
|
Л |
И |
Л |
Л |
|
a4 |
Л |
Л |
И |
И |
|
И |
И |
И |
И |
|
a5 |
И |
Л |
Л |
И |
|
Л |
И |
Л |
Л |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
Л |
И |
И |
|
И |
И |
И |
И |
|
a2 |
И |
Л |
Л |
И |
|
Л |
Л |
Л |
И |
|
a3 |
И |
Л |
Л |
И |
|
Л |
Л |
Л |
И |
|
a4 |
И |
Л |
Л |
И |
|
И |
Л |
Л |
И |
10
|
a5 |
И |
Л |
И |
И |
|
И |
И |
Л |
Л |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
И |
Л |
И |
|
И |
Л |
Л |
И |
|
a2 |
Л |
Л |
И |
Л |
|
И |
И |
И |
И |
|
a3 |
И |
Л |
И |
Л |
|
И |
И |
Л |
И |
|
a4 |
И |
И |
Л |
И |
|
Л |
Л |
Л |
И |
|
a5 |
И |
Л |
И |
Л |
|
Л |
Л |
И |
Л |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
И |
Л |
Л |
|
Л |
Л |
И |
Л |
|
a2 |
И |
И |
И |
И |
|
Л |
И |
И |
Л |
|
a3 |
И |
И |
И |
И |
|
Л |
Л |
Л |
Л |
|
a4 |
И |
Л |
И |
Л |
|
Л |
Л |
Л |
Л |
|
a5 |
Л |
Л |
Л |
Л |
|
Л |
Л |
И |
И |
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
Л |
Л |
И |
|
И |
Л |
Л |
Л |
|
a2 |
Л |
И |
И |
Л |
|
И |
Л |
Л |
И |
|
a3 |
Л |
И |
Л |
Л |
|
И |
И |
Л |
Л |
|
a4 |
И |
Л |
И |
Л |
|
И |
Л |
Л |
Л |
|
a5 |
Л |
И |
Л |
И |
|
Л |
Л |
И |
Л |
6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
Л |
И |
Л |
И |
|
И |
И |
И |
И |
|
a2 |
Л |
И |
И |
И |
|
И |
И |
И |
Л |
|
a3 |
Л |
И |
И |
И |
|
И |
Л |
Л |
Л |
|
a4 |
И |
Л |
Л |
И |
|
И |
И |
И |
И |
|
a5 |
И |
Л |
Л |
И |
|
Л |
Л |
Л |
Л |
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
b1 |
b2 |
b3 |
b4 |
|
b5 |
b6 |
b7 |
b8 |
|
a1 |
И |
Л |
Л |
И |
|
И |
И |
И |
Л |
|
a2 |
И |
И |
Л |
Л |
|
Л |
И |
И |
Л |
|
a3 |
И |
И |
Л |
И |
|
И |
И |
И |
Л |
