- •Мультимедийные лекции
- •Содержание
- •Лекция 1.Множества Элементы теории множеств. Операции над множествами.
- •Операции над множествами.
- •Лекция 2. Функция Понятие функции. Основные свойства функции.
- •Основные элементарные функции и их графики.
- •Лекция 3.Предел последовательности Числовые последовательности. Пределчисловойпоследовательности.
- •Лекция 4.Предел функции Предел функции в точке и в бесконечности. Основные теоремы о пределах.Бесконечно малые и бесконечно большие функции.
- •Бесконечно малые и бесконечно большие функции.
- •Основные теоремы о пределах функций.
- •Лекция 5.Техника вычесления пределов Замечательные приделы.
- •Первый замечательный предел.
- •Техника дифференцирования:
- •Примеры применения производной в экономике.
- •Лекция 7. Приложения производной к исследованию функций и построению графиков. Исследование функции на монотонность (возрастание и убывание функции)
- •Экстремум функции (исследование функции на экстремум)
- •Наибольшее и наименьшее значение функции на отрезке.
- •Исследование функции на выпуклость и точку перегиба.
- •Асимптоты графика функции. Исследование функции на асимптоты.
- •Общая схема исследования функций и построения графиков.
- •Лекция 8. Первообразная функция. Неопределенный интеграл и его свойства.
- •Свойства неопределенного интеграла и его геометрические свойства.
- •Основные приемы интегрирования
- •Лекция 10.Интегрирование тригонометрических функций.
- •Интегрирование некоторых видов иррациональных функций.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Лекция 14.Линейные дифференциальные уравненияпервого порядка.
- •Лекция 15.Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •Лекция 16.Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Лекция 17.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и правой частью специального вида.
- •Лекция 18. Числовые ряды.Сумма ряда.
- •Эталонные ряды.
- •Признаки сходимости знакоположительных рядов
- •Достаточные признаки
- •Лекция 19. Знакопеременные ряды. Понятие абсолютной и условной сходимости знакопеременого ряда.
- •Лекция 20. Степенные ряды. Область сходимости. Теорема н. Абеля.
- •Свойства степенных рядов
- •Ряд Маклорена. Ряд Тейлора.
Лекция 4.Предел функции Предел функции в точке и в бесконечности. Основные теоремы о пределах.Бесконечно малые и бесконечно большие функции.
Пусть функция y =f(x) определена в некоторойокрестностиx0,кроме, может быть, самой точки x0.
Определение. ЧислоA называется пределом функцииy =f(x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε> 0найдетсятакоечисло δ> 0, что для всех х x0, удовлетворяющих неравенству
│ х –x0│< δ, выполняется неравенство│f(x) –А│<ε.
Или кратко:
![]() ε>
0
ε>
0
![]() δ
> 0,
δ
> 0,
![]() x:│
х –x0│<
δ, х x0>
│f(x)
–А│<ε.
x:│
х –x0│<
δ, х x0>
│f(x)
–А│<ε.

Геометрический
смысл предела
функции заключается в следующем: число
 ,
если для любой ε
– окрестности точкиAнайдется
такая δ –
окрестность точки x0,
что для всех х
x0
из этой окрестности соответствующие
значения функции f(x)
лежат в ε –
окрестности точки А.
,
если для любой ε
– окрестности точкиAнайдется
такая δ –
окрестность точки x0,
что для всех х
x0
из этой окрестности соответствующие
значения функции f(x)
лежат в ε –
окрестности точки А.

Рис. 1
Пример:Доказать,
что

Решение.
Возьмем произвольное
 и найдем
и найдем
 такое,
что для всехx,
удовлетворяющих неравенству,
такое,
что для всехx,
удовлетворяющих неравенству,
 ,
выполняется неравенство
,
выполняется неравенство ,
то есть
,
то есть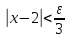 .
.
Взяв
 ,
видим, что для всехx,
удовлетворяющих неравенству,
,
видим, что для всехx,
удовлетворяющих неравенству,
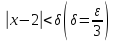 ,
выполняется неравенство
,
выполняется неравенство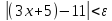 ,
следовательно,
,
следовательно,

Пусть
функция y
=f(x)
определена в промежутке (– ;
+
;
+ ).
).
Определение.
ЧислоA
называется пределом
функцииf(x)
при х

 ,
если для любого числа ε
>
0существуеттакоечисло M
= M
(ε) > 0, что
для всех значений x,
удовлетворяющих неравенству
│x│>M,выполняется
неравенство │f(x)
– А│<
ε. В этом
случае пишут
,
если для любого числа ε
>
0существуеттакоечисло M
= M
(ε) > 0, что
для всех значений x,
удовлетворяющих неравенству
│x│>M,выполняется
неравенство │f(x)
– А│<
ε. В этом
случае пишут
 f(x)
= А.
f(x)
= А.
Или кратко:
![]() ε>
0
ε>
0
![]() M>
0, │x│
>M>
│f(x)
–А│<ε.
M>
0, │x│
>M>
│f(x)
–А│<ε.
 f(x)
= А.
f(x)
= А.
Бесконечно малые и бесконечно большие функции.
Определение
1. Функция
f(x)
называется бесконечно
большойфункцией
при х →x0,
если
 f(x)
=
f(x)
=
 .
.
Определение
2. Функцияf(x)
называется бесконечно
малой функцией
при х →x0,
если
 f(x)
= 0.
f(x)
= 0.
Основные теоремы о пределах функций.
Теорема 1. Предел постоянной величины равен самой постоянной:
 c
= c.
c
= c.
Теорема 2. Пределсуммы (разности) двух функций равен сумме (разности) их пределов:

 =
=
 f(x)
f(x)
 φ(x).
φ(x).
Теорема 3.Пределпроизведения двух функций равен произведению их пределов:

 =
=
 f(x)
f(x)
 φ(x).
φ(x).
Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:

 ,
,


0.
0.
Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x0выполняются неравенства:
 и
и
 =
=
 =А,
то
=А,
то
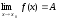 .
.
Лекция 5.Техника вычесления пределов Замечательные приделы.
Пример 1.

Будем
говорить, что предел отношения двух
функций
 есть неопределенность вида
есть неопределенность вида
 или
или ,
если числитель и знаменатель дроби
одновременностремятся к нулю или к
бесконечности. Раскрыть эти неопределенности
– значит вычислить предел отношения
,
если числитель и знаменатель дроби
одновременностремятся к нулю или к
бесконечности. Раскрыть эти неопределенности
– значит вычислить предел отношения ,
если он существует или установить, что
этот предел не существует.
,
если он существует или установить, что
этот предел не существует.
Пример
2.


Из
рассмотренного примера следует правило:
чтобы раскрыть неопределенность вида
 приx→x0
функции, заданной в виде отношения двух
многочленов, необходимо в числителе и
знаменателе выделить множитель x−x0
и дробь на него сократить.
приx→x0
функции, заданной в виде отношения двух
многочленов, необходимо в числителе и
знаменателе выделить множитель x−x0
и дробь на него сократить.
При
вычислении пределов отношения двух
многочленов при x→ для
раскрытия неопределенности вида
для
раскрытия неопределенности вида надо
числитель и знаменатель дроби разделить
наx
в старшей степени.
надо
числитель и знаменатель дроби разделить
наx
в старшей степени.
Пример 3.

Пример 4.