Лекция 20. Степенные ряды. Область сходимости. Теорема н. Абеля.

Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции.

Определение 1. Степенным рядом называется ряд вида:

где aи коэффициенты а₀,… ,а_n – постоянный.

При а=0 степенной ряд примет вид:

Определение 2.Совокупность значений x, при которых степенной ряд сходится, называется областью сходимостью степенного ряда.

Пример. Найти область сходимости.

1+x+ x² + … + xⁿ +…

Это геометрический рядq = x. Он сходится при то есть приилиследовательно, область сходимости (−1; 1).

Структура области сходимости степенного ряда устанавливается с помощью теоремы Н. Абеля:

1. Если степенной ряд (2) сходится приx = x₀≠ 0, то он абсолютно сходится и при всех значениях x, удовлетворяет неравенству .

2. Если степенной ряд (2) расходится приx = x₁≠ 0, то он расходится и при всех значениях x, удовлетворяет неравенству .

Из теоремы Н. Абеля следует, что существует такое число R ≥ 0, что при всех ряд (2) сходится, а прирасходится.

Число Rназывается радиусом сходимости степенного ряда, а интервал (−R; R) называется интервалом сходимости.

На концах интервала сходимости ряд (2) может, как сходится, так и расходится.

Для ряда (1) получим:

, то есть .Следовательно, интервал сходимости ряда (1) имеет вид:.

Радиус сходимости степенного ряда находится по формуле:

Пример 1.

Решение:

Тогда

Следовательно, (−2; 2) – интервал сходимости.

При ряд расходится, так как

То есть

Следовательно,при ряд расходится.

Пример 2.

Решение:

Тогда (−1;1) – интервал сходимости.

При x=1ряд расходится, как обобщенный гармонический.

При x=−1 получим знакочередующийся ряд.

На основании признака Лейбница он сходится, т.к.

Следовательно, область сходимости −1≤x˂1

Свойства степенных рядов

Пусть степенной ряд

имеет интервал сходимости.

Тогдаряд, полученный из данного ряда почленным дифференцированием или интегрированием, имеет тот же интервал сходимости.

Следовательно, на интервале сходимости степенные ряды можно почленно дифференцировать и интегрировать.

Ряд Маклорена. Ряд Тейлора.

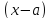Если функцияразлагается в степенной ряд по степеням, то ряд имеет следующий вид:

Этот ряд называется рядом Тейлора.

В частном случае при a=0 ряд примет вид:

Этот ряд называется рядом Маклорена.

Разложение в степенные ряды элементарных функций