Свойства векторного произведения.

1. ×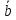=‒ (×)– не коммутативно

2. Если коллинеарен , то×=, т. к.sin 0⁰ = 0.

3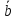.  (×) = ( · ) ×=× ( · ) – ассоциативность

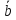4. (+) ×=×+×– дистрибутивность

Выражение векторного произведения через координаты.

Пусть = ();= ();

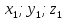Разложим а и b по базисным векторам:

а= x₁i + y₁ j + z₁k,     b = x₂i + y₂ j + z₂k.

Используя свойства векторного произведения, получаем

× = (x₁i + y₁ j+ z₁k)× (x₂i + y₂ j+ z₂k) =

= x_1·x_2·i×i + x_1·y_2·i×j + x_1·z₂·i×k +

+ y_1·x₂ j×i + y_1·y₂ j; j + y_1·z₂ j×k +

+ z_1·x₂ k×i + z_1·y₂ k×j + z_1·z₂ k×k.      (1)

По определению векторного произведения находим

i×i = 0,         i×j = k,           i×k= –j,

j×i = –k,      j×j  = 0,          j×k  = i,

k×i = j,         k×j = –i.      k×k = 0.

Учитывая эти равенства, формулу (1) можно записать так:

× =x₁y₂k–x₁z₂ j–y₁x₂k + y₁z₂ i + z₁x₂ j –z₁y₂i

или

× = (y₁z₂ –z₁y₂) i + (z₁x₂ –x₁z₂ )j + (x₁y₂–y₁x₂) k.   (2)

Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами.

Полученную формулу можно записать в другом более удобном для запоминания виде:

× =  (3)

Обычно формулу (3)  записывают еще короче:

× =(4)

‒ формула для вычисления векторного произведения.

Тогда,

S_{пароаллелограмма} = │×│=

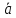S_{треугольника =} =;

Пример: найти векторное произведение векторов:

Решение:

Смешанное произведение векторов (геометрический смысл, свойства).

Смешанным произведением векторов( × ) называется скалярноепроизведениевектора( × )на вектор.

Геометрический смысл

Построим на векторах , параллелепипед и найдем его объемV.

V_{параллелепипеда} = S_осн. · H = ·=··Cos= .

= V_{параллелепипеда}

Модульсмешанногопроизведениятрехвекторов численно равен объему параллелепипеда, построенного натрехданных векторах ‒ множителях.

V_{тетраэдра} = V_{параллелепипеда}

Выражение векторного и смешанного произведения через координаты перемножаемых векторов.

Пусть = ();= ();

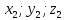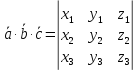
‒ формула для вычисления смешанного произведения.

Пример:

Дано: ABCD – тетраэдр. A (– 2; 3; – 4) B (3; – 1; 5) C (4; – 4; 2) D (5; 7; 1) Найти: 1) ABC 2) Уравнение BCD 3) VABCD

Решение:

1)

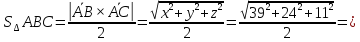
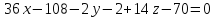
2)

│: 2

–уравнение BCD.

3)

кубических единиц.

Теорема. Признак компланарности векторов.

Для того чтобы векторы , были компланарны, необходимо и достаточно чтобы ихсмешанное произведение равнялось нулю, т.е.

,

т.к. объем V_{параллелепипеда} = 0 (векторы , в одной плоскости).

Пример: Проверить компланарны ли три вектора

= {1; 1; 1}, = {1; 3; 1},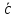= {2; 2; 2}.

Решение: найдем смешанное произведение векторов.

· [×] =

Ответ: вектора компланарны, так как их смешанное произведение равно нулю.

Уравнение плоскости, проходящей через три данные точки.

Пусть плоскость проходит через точки М₁ = (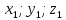),М₂ = () иМ₃ = (), не лежащие на одной прямой иМ (x, y, z)  – произвольная точка плоскости.

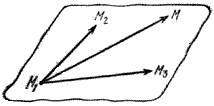
Векторы ,и‒ компланарные, т.к. находятся в одной плоскости. Следовательно,

· ·= 0.

Запишем это равенство в координатной форме:

‒ уравнение плоскости проходящей через три данные точки.

Понятие векторного (линейного) пространства. Вектор вn‒ мерном пространстве.

n ‒ мерным вектором называется упорядоченная совокупность n ‒ действительных чисел, записываемых в виде:

= (,, …,),

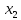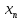где ‒i‒ компонента вектора =.

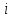Для n ‒ мерных векторов имеют место операции сложения и умножения на число, удовлетворяющие следующим свойствам:

1. +=+– коммутативность;

2. + (+) = (+) +– ассоциативность;

3. (= ()– ассоциативность;

4.  (+) = +  – дистрибутивность;

5. + (‒) =.

Линейным векторным пространством называется совокупность n ‒ мерных векторов с действительными компонентами, удовлетворяющих приведенным выше свойствам.