Исследование систем линейных уравнений. Теорема Кронекера - Капелли, базисные решения.

Теорема 1(Кронекера-Капелли). Система m – линейных уравнений с n – неизвестными совместна только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

r (A) = r (A_в)

Пример:

│А│= = 65 0, r (А) = 3;

A_B= =r (A_B) ≤ 3, так как

= ‒ 8 + 45 + 144 ‒ 40 + 72 ‒ 18 = 195 =r (A_B) = 3 =

r(A) = r (A_B) => по теореме Кронекера ‒ Капелли система совместна.

Теорема 2. Если ранг матрицы совместной системы равен числу неизвестных, т. е. r(A) = n, то система имеет единственное решение.

Если ранг матрицы системы меньше числа неизвестных, т. е. r (A) < n, то система имеет множество решений.

Тогда переменные х₁, х₂, …, х_r называются базисными, если минор, составленный из коэффициентов при этих неизвестных  0, остальные (n – r) – неизвестных называются свободными.

Пример: найти базисное решение системы уравнений.

Решение:

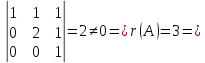х₁, х₂, х₃ – базисные, х₄ – свободная.

Пусть х₄= C = const; х₃= 2, тогда

2 х₂+ 2 + 2 C= 0 | · 2

х₂= – C – 1

х₁ – C – 1 + 2 + C= 2;

х₁= 1

Ответ:

х₁= 1;

х₂= – C – 1;

х₃ = 2;

х₄= C.

Найдем частное решение:

Пусть C = 1, тогда

х₁= 1;

х₂= – 2;

х₃ = 2;

х₄= 1.

Проверка:

Подставим значения х₁, х₂, х₃, и х₄ в систему уравнений

,

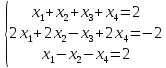Получим

Системы линейных однородных уравнений. Исследование решений. Фундаментальная система решений.

Однородной системой m – линейных уравнений с n – неизвестными называется система уравнений вида:

Теорема. Система (3) всегда имеет хотя бы одно тривиальное решение: х₁= х₂ = … = х_n= 0.

При решении однородной системы линейных уравнений возможны следующие случаи:

1) Если m = n и определитель матрицы системы ∆  0, то ∆ x₁ = ∆ x₂ = = … = ∆ x_n= 0. Тогда система (3) имеет единственное тривиальное решение х₁= х₂ = … = х_n= 0 - по формулам Крамера.

2) Если m = n, но определитель матрицы системы ∆ = 0, то система (3) имеет множество решений.

3) Если m<n, то система (3) имеет множество решений.

Определение. Система линейно независимых решений e_l, е₂, ..., е_k называется фундаментальной, если каждое решение системы (3) является линейной комбинацией решений e_l, е₂ , ..., е_k.

Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (3) меньше числа пере­менных n, то всякая фундаментальная система решений систе­мы (3) состоит из n – r решений.

Пример:

m = 3; n = 4.

х₁, х₂, х₃ – базисные, x₄ – свободное.

Пустьх₄= C, тогда

х₃ = х₄=>х₃= C

х₂– 7C– 14C= 0

х₂= 21C

х₁– 21C + 2C + 5C = 0

х₁= 14C

Ответ:

х₁= 14C;

х₂= 21C;

х₃= C;

х₄= C.

Модель Леонтьева многоотраслевой экономики. Продуктивные модели Леонтьева.

Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)

Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой — потребителем продукции, выпускаемой другими отраслями. Возникает довольно непростая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 г. в трудах известного американского экономиста В. В. Леонтьева, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.