Элементарные преобразования матрицы.

К элементарным преобразованиям матрицы относятся:

1. Изменение порядка строк (столбцов).

2. Отбрасывание нулевых строк (столбцов).

3. Умножение элементов любой строки (столбца) на одно число.

4. Прибавление к элементам любой строки (столбца) элементов другой строки (столбца), умноженных на одно число.

Системы линейных алгебраических уравнений слу (Основные понятия и определения).

1. Системой m линейных уравнений с n неизвестными называется система уравнений вида:

2. Решением системы уравнений (1) называется совокупность чисел x₁, x₂, … , x_n, обращающая каждое уравнение системы в тождество.

3. Система уравнений (1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной.

4. Система уравнений (1) называется определенной, если она имеет только одно решение, и неопределенной, если у нее более одного решения.

5. В результате элементарных преобразований система (1) преобразуется к равносильной ей системе (т.е. имеющей то же множество решений).

К элементарным преобразованиям систем линейных уравнений относятся:

1. Отбрасывание нулевых строк.

2. Изменение порядка строк.

3. Прибавление к элементам любой строки элементов другой строки, умноженных на одно число.

Методы решения систем линейных уравнений.

1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.

Системой n линейных уравнений с n неизвестными называется система уравнений вида:

Запишем систему (2) в матричном виде, для этого введем обозначения.

Матрица коэффициентов перед переменными:

X = ‒ матрица переменных.

В = ‒ матрица свободных членов.

Тогда система (2) примет вид:

A×X = B ‒ матричное уравнение.

Решив уравнение, получим:

X = A^-1×B

Пример:

; ;

1) │А│= 15 + 8 ‒18 ‒9 ‒12 + 20 = 4  0 матрицаА^-1 существует.

2) A^T= ;

3)

à =

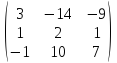
4) А^-1 = × Ã =;

Х = А^-1 × B

Ответ:

2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.

Рассмотрим систему 2 ‒ х линейных уравнений с 2 ‒ мя неизвестными:

Решим эту систему методом подстановки:

Из первого уравнения следует:

Подставив во второе уравнение, получим:

Подставляем значение в формулу для, получим:

=

Определитель Δ — определитель матрицы системы;

Δ x₁ — определитель переменной x₁;

Δ x₂ — определитель переменной x₂;

Формулы:

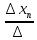x ₁ =;x ₂ =;…,x_n = ;Δ  0;

‒ называются формулами Крамера.

При нахождении определителей неизвестных х₁, х₂,…, х_nзаменяется столбец коэффициентов при той переменной, определитель которой находят, на столбец свободных членов.

Пример: Решить систему уравнений методом Крамера

Решение: 

Составим и вычислим сначала главный определитель этой системы:

Так как Δ ≠ 0, то система имеет единственное решение, которое можно найти по правилу Крамера:

где Δ ₁, Δ ₂, Δ ₃ получаются из определителя Δ путем замены 1‒ го, 2 ‒ го или 3 ‒ го столбца, соответственно, на столбец свободных членов.

Таким образом:

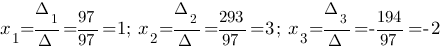
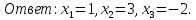
Метод Гаусса решения систем линейных уравнений.

Рассмотрим систему:

Расширенной матрицей системы (1) называется матрица вида:

Метод Гаусса – это метод последовательного исключения неизвестных из уравнений системы, начиная со второго уравнения по m – тое уравнение.

При этом путем элементарных преобразований матрица системы приводится к треугольной (если m = n и определитель системы ≠ 0) или ступенчатой (если m < n) форме.

Затем, начиная с последнего по номеру уравнения, находятся все неизвестные.

Алгоритм метода Гаусса:

1) Составить расширенную матрицу системы, включающую столбец свободных членов.

2) Если а₁₁  0, то первую строку делим на а₁₁ и умножаем на (– a₂₁) и прибавляем вторую строку. Аналогично дойти до m–той строки:

I стр. делим на а₁₁ и умножаем на (– а_m1) и прибавляем m – тую стр.

При этом из уравнений, начиная со второго по m – тое, исключится переменная x₁.

3) На 3 ‒ м шаге вторая строка используется для аналогичных элементарных преобразований строк с 3 ‒ й по m – тую. При этом исключится переменная x_{2 ,} начиная с 3 ‒ й строки по m – тую, и т. д.

В результате этих преобразований система приведется к треугольной или ступенчатой форме (в случае треугольной формы под главной диагональю нули).

Приведение системы к треугольной или ступенчатой форме называется прямым ходом метода Гаусса, а нахождение неизвестных из полученной системы называется обратным ходом.

Пример:

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицыA_b, получим матрицу:

Сложим вторую строку полученной матрицы с первой, умноженной на (‒2), а её третью строку – с первой строкой, умноженной на (‒7). Получим матрицу

К третьей строке полученной матрицы прибавим вторую строку, умноженную на (‒3), в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:

,

Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных: