
- •Мультимедийные лекции
- •Содержание
- •Основные сведения о матрицах.
- •Виды матриц
- •Операции над матрицами и их свойства.
- •Правило Саррюса (правило треугольника).
- •Теорема Лапласа
- •Свойства определителей.
- •Вырожденные и невырожденные матрицы, обратная матрица.
- •Решение матричных уравнений.
- •Ранг матрицы, нахождение ранга матрицы.
- •Элементарные преобразования матрицы.
- •Системы линейных алгебраических уравнений слу (Основные понятия и определения).
- •Методы решения систем линейных уравнений.
- •1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.
- •2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.
- •Метод Гаусса решения систем линейных уравнений.
- •Исследование систем линейных уравнений. Теорема Кронекера - Капелли, базисные решения.
- •Системы линейных однородных уравнений. Исследование решений. Фундаментальная система решений.
- •Модель Леонтьева многоотраслевой экономики. Продуктивные модели Леонтьева.
- •Балансовые соотношения
- •Линейная модель многоотраслевой экономики
- •Векторы (основные понятия и определения).
- •Сложение векторов
- •Разность векторов
- •Линейные операции над векторами. Направляющие косинусы.
- •Прямоугольный базис.
- •Декартова прямоугольная система координат в пространстве.
- •Прямоугольные координаты вектора (точки).
- •Разложение вектора по базису.
- •Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
- •Векторное произведение векторов (геометрический смысл, свойства).
- •Свойства векторного произведения.
- •Выражение векторного произведения через координаты.
- •Смешанное произведение векторов (геометрический смысл, свойства).
- •Выражение векторного и смешанного произведения через координаты перемножаемых векторов.
- •Уравнение плоскости, проходящей через три данные точки.
- •Понятие векторного (линейного) пространства. Вектор вn‒ мерном пространстве.
- •Размерность и базис векторного пространства.
- •Линейная оболочка и ее свойства.
- •Свойства линейной оболочки
- •Евклидово пространство.
- •Ортогональный и ортонормированный базис.
- •Переход к новому базису.
- •Линейные операторы.
- •Собственные векторы и собственные значения линейного оператора (матрицы).
- •Квадратичные формы.
- •Линейная модель обмена (международной торговли).
- •Уравнения прямой (различные виды). Параметрические уравнения прямой.
- •Уравнение прямой проходящей через две данные точки.
- •Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
- •Общее уравнение прямой.
- •Формула угла между прямыми.
- •Условия параллельности и перпендикулярности прямых.
- •Формула расстояния от точки до прямой.
- •Комплексные числа. Алгебраическая форма комплексного числа.
- •Действия над комплексными числами в алгебраической форме.
Правило Саррюса (правило треугольника).

Пример 1:
 =
–
2×1×
(–5)
+ 5×4×(–
4)
+ 3×2×(–
3)
–
(–
3)
×1× (–
4)
–
4×2×
=
–
2×1×
(–5)
+ 5×4×(–
4)
+ 3×2×(–
3)
–
(–
3)
×1× (–
4)
–
4×2×
(– 2) – 5×3 × (– 5) = 10 – 80 –18 –12 +16 +75 = – 9.
Пример 2:
 =
45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.
=
45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.
Минором Mij элемента aijквадратной матрицы n ‒ го порядка называется определитель (n ‒ 1) ‒ го порядка, полученный из данной матрицы вычеркиванием i ‒ й строки и j ‒ го столбца, на пересечении которых стоит данный элемент.
Пример:
 ;
;
M11
=
 = 15 + 2 = 17;
= 15 + 2 = 17;
M12
=
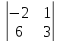 = –
6
–
6
= –12;
и т. д. всего 9 миноров.
= –
6
–
6
= –12;
и т. д. всего 9 миноров.
Алгебраическим дополнением Aijэлемента aij квадратной матрицы называется его минор, взятый со знаком (‒1)i+j.
Пример:

А 11 = (–1)1+1 × M11 = 17.
А 12 = (–1)1+2 × M12 = ‒ 1×M12 = 12.
А
13 =
(–1)1+3
×
 =
4 ‒ 30= – 26; и т.д.
=
4 ‒ 30= – 26; и т.д.
Теорема Лапласа
Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
 по
I
стр. =
по
I
стр. =
 ×
(–1)
1+2
×
×
(–1)
1+2
×
 +
+ ×(–1)
1+2
×
×(–1)
1+2
×
×
 +
+ ×(–1)
1+2×
×(–1)
1+2×
 ;
;
Пример:
 по
II
стр. = ‒ 2×(–1)2+1
×
по
II
стр. = ‒ 2×(–1)2+1
×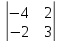 +5×(–1)2+2
×
+5×(–1)2+2
× +1×
+1×
×(–1)
2+3× =
2×(–12+4)+5×(9–12)–1×(–6+24) = 16–15–18= – 49.
=
2×(–12+4)+5×(9–12)–1×(–6+24) = 16–15–18= – 49.
Свойства определителей.
1. Определитель равен нулю, если содержит:
- нулевую строку или нулевой столбец;
- две одинаковые строки (столбца);
- две пропорциональных строки (столбца).
Пример:
 =
0;
=
0;
 = 0;
= 0; = 0;III
= I
× (-3).
= 0;III
= I
× (-3).
2. Общий множитель элементов любой строки (столбца) можно выносить за знак определителя.
Пример:
 =
2×
=
2× = 2×(30+24+4‒24+8+15) = 2×57= 114.
= 2×(30+24+4‒24+8+15) = 2×57= 114.
3. Определитель не изменится, если к элементам любой строки (столбца) прибавить элементы другой строки (столбца) умноженные на одно число.
Пример:
 I
× 5 + II; I × (‒2) + III; I × (‒ 4) + IV;
I
× 5 + II; I × (‒2) + III; I × (‒ 4) + IV;
=
 = 1×(–1)1+3×
= 1×(–1)1+3× .
.
Вырожденные и невырожденные матрицы, обратная матрица.
Матрица А-1называется обратной к матрице A, если при умножении ее на матрицу A, как справа, так и слева, получится единичная матрица.
А-1×A=A× А-1=E
Матрица называется невырожденной, если ее определитель не равен 0, и называется вырожденной, если ее определитель равен 0.
Теорема.
Обратная матрица А-1существует только тогда, когда матрица невырожденная, т.е. |A| ≠ 0.
Алгоритм нахождения.
1. Найти определитель матрицы А.
Если │A│= 0, то обратная матрица не существует, если │A│≠ 0, то перейти ко второму шагу.
2. Найти матрицу AT, транспонированную к матрице А.
3. Найти алгебраические дополнения элементов матрицы AT и составить из них матрицу Ã, которая называется присоединенной.
Ã
=

4. Обратную матрицу найти по формуле:

5. Сделать проверку А-1 × A = E
Решение матричных уравнений.
Матричное уравнение имеет вид:
A × Х= B
Умножим обе части уравнения на матрицу А-1 слева:
А-1× A ×Х = А-1 × В.
Так как А-1×А=Е, то Е×Х = А-1×В.
Так какЕ × Х=X, то Х= А-1×В
Пример:
Дано:
А
=
 ;
;
В
=
 ;
;
Найти:
X ‒?
Решение:
1)
│А│=

2)
AT=
 .
.
3)



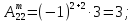
Ã=
 .
.
4)
А-1
=
 × Ã =
× Ã = ×
× =
=
Х=
А-1×
B
=


Ответ:
Ранг матрицы, нахождение ранга матрицы.
Рангом матрицы называется наивысший порядок не равных нулю миноров этой матрицы.
Обозначается rang (A) или r (A).
Теорема 1. Ранг матрицы не превосходит наименьшего из ее размеров.
r(A) ≤ min (m; n)
Пример:
А2×3
=
 ;
;
r (A) ≤ min (2; 3) = 2, т. е. согласно теореме r (A) ≤ 2.
 =
3 + 24 = 27
0; r
(A)
= 2 (порядок ненулевого минора).
=
3 + 24 = 27
0; r
(A)
= 2 (порядок ненулевого минора).
Теорема 2. Ранг квадратной матрицы n-го порядка равен ее порядку, если она не вырожденная.
Примеры:
1)А3×3
=
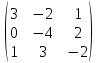 ;
r
(A)
≤ 3.
;
r
(A)
≤ 3.
│А│=
 = 24 + 0 – 4 + 4 – 18 – 0 = 6
0
= 24 + 0 – 4 + 4 – 18 – 0 = 6
0
 матрица не вырожденная
матрица не вырожденная r
(A)
= 3.
r
(A)
= 3.
2)А3×3
= ;
│А│=
0, т.к.
III = I × (– 3)
;
│А│=
0, т.к.
III = I × (– 3)
 r
(A)
< 3.
r
(A)
< 3.
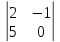 =
0 + 5 = 5
0
=
0 + 5 = 5
0
 r
(A)
= 2 (порядок ненулевого минора).
r
(A)
= 2 (порядок ненулевого минора).
Теорема 3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
