Квадратичные формы.

Пусть L = () ‒ симметричная матрицаn‒ го порядка, т.е. =.

Определение. Выражение

называется квадратичной формой переменных x₁, x₂, …, x_n.

Выра­жение (1) есть сумма всех квадратов переменных плюс сумма всех удвоенных произведений разных переменных, причем каждый член суммы взят с некоторым коэффициентом. Матрица L назы­вается матрицей квадратичной формы.

Построим квадратичную форму. Введем матрицу ‒ столбец переменных

матрицу ‒ строку этих переменных X^m = (x₁, x₂, …, x_n) и найдем произведение матриц:

После перемножения получим

Следовательно, в матричной форме квадратичная форма может быть представлена в виде

= X^T ·L ·X .

Матрице ‒ столбцу переменных можно поставить в соответствие вектор х, координатами которого в ортобазисе e₁, е₂, …, е_n, будут элементы матрицы ‒ столбца. Тогда выражение (1) можно интерпретировать как числовую функцию векторного аргумента х: (х).

Пример: Найти матрицу квадратичной формы

(x)= ‒ +6‒ 3+4+‒3

Решение: Общий вид заданной квадратичной формы

(x)= +++++

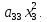
Поэтому

= .

Пусть оператор переводит векторв вектор. Поскольку действие линейного операторана векторсводится к умножению некоторой матрицыP = (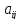) на матрицу ‒ столбецY, составленную из координат вектора , запишем линейное преобразование в матричном виде:

Х = P· Y.

Выясним, как изменяется матрица квадратичной формы при линейном преобразовании векторов х → у:

(x) = где=.

Пусть дополнительно выполняется условие невырожденности матрицы оператора | Р|  0 и квадратичная форма является числовой функцией вектора :(y) = .

Найдем, как изменяется матрица квадратичной формы при линейном преобразовании векторов у → х. Решим матричное уравнение

Х = P · Y,

умножив обе части равенства слева на .

Тогда

(y) = =

где .

Пример: Как изменится матрица квадратичной формы

(x) = ‒+ 2+ 3при линейном преобразовании векторов

.

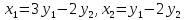Решение:Матрица заданной квадратичной формы равна

матрица линейного оператора при линейном преобразовании векторовх = (у) имеет вид .

Под действием линейного оператора матрица квадратичной формы станет равной ,

а квадратичная форма примет более простой вид:

(y) = .

Линейная модель обмена (международной торговли).

Пусть имеется n ‒ стран ,, …,, национальный доход которых обозначим соответственно,, …,.

Обозначим – долю национального дохода, которуюj – страна тратит на закупку товаров у i –страны. (i = ;j= )

Предположим, что весь национальный доход тратится либо на закупку товаров внутри страны, либо на импорт их из других стран.

Получим структурную матрицу торговли:

Из равенства (1) следует, что сумма элементов любого столбца матрицыАравна единице.

Для любой страны выручка от внутренней и внешней торговли будет находиться по формуле:

= ++ … +.

Для сбалансированной торговли нужна бездефицитность торговли каждой страны , т.е. выручка от торговли должна быть не меньше ее национального дохода:

(2)

Запишем неравенство (2) в виде системы линейных неравенств:

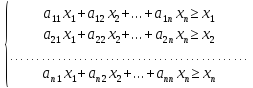(3)

Сложив левые и правые части неравенств системы, получим:

(++ … +)+ (++ … +)+ … + (++ … +)++ … +.

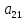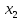Учитывая равенство (1) получим, что левая часть неравенства равна правой части, и система неравенств (3) станет системой уравнений.

A · X = XA · X – X = 0; (A – E) · X = 0

Задача свелась к нахождению собственного вектора матрицы A при = 1.

Пример: Структурная матрица торговли четырех стран име­ет вид:

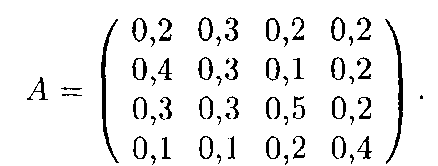
Найти бюджеты этих стран, удовлетворяющие сбалансиро­ванной бездефицитной торговле при условии, что сумма бюд­жетов задана:

Решение: Необходимо найти собственный вектор , отве­чающий собственному значению λ = 1 заданной структурной матрицыА, т.е. решить уравнение, которое в нашем случае имеет вид:

Поскольку ранг этой системы равен трем, то одна из неизвест­ных является свободной переменной и остальные выражаются через нее. Решая систему методом Гаусса, находим компонен­ты собственного вектора :

Подставив найденные значения в заданную сумму бюджетов, найдем величину с: с = 1210, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):