
- •Оглавление
- •Условные обозначения
- •Предисловие
- •Задачи биостатистики
- •Основные понятия и определения биостатистики
- •Классификация признаков
- •Анализ медико-биологических данных на основе их графического представления
- •Анализ медико-биологических данных на основе числовых статистических характеристик
- •Свойства нормального распределения
- •Теория проверки статистических гипотез
- •I алгоритм
- •II алгоритм
- •Проверка гипотезы о нормальности распределения случайной величины
- •Параметрические критерии проверки статистических гипотез
- •Анализ относительных величин
- •Доверительный интервал
- •Доверительный интервал для разности генеральных средних двух независимых групп
- •Доверительный интервал для разности генеральных средних двух зависимых групп
- •Доверительный интервал относительных показателей
- •Непараметрические критерии проверки статистических гипотез
- •Анализ качественных признаков. Таблицы сопряженности
- •Оценка факторов риска
- •Оценка чувствительности и специфичности диагностических тестов
- •Оценка прогностического значения диагностических тестов
- •Однофакторный дисперсионный анализ
- •Линейная корреляция
- •Коэффициент корреляции рангов к. Спирмена
- •Линейная регрессия
- •Анализ выживаемости
- •Методы прогнозирования
- •Методы простой экстраполяции
- •Метод среднего абсолютного прироста
- •Метод среднего темпа роста
- •Прогнозирование на основе математических моделей
- •Оценка факторов риска и прогнозирование на основе логистической регрессии
- •Анализ качественных признаков на основе логлинейной модели
- •Байесовский подход к диагностике и прогнозированию. Последовательный анализ вальда
- •Определение размера выборки
- •Расчет объема выборки при эпидемиологических исследованиях
- •Представление статистических данных в научных публикациях
- •Заключение
- •Список литературы
- •Приложение 1. Критические значения коэффициента асимметрии As
- •Приложение 2. Критические точки двустороннего tкритерия Стьюдента
- •Приложение 3. Критические значения Uкритерия МаннаУитни
- •Приложение 4. Критические значения парного Ткритерия Уилкоксона
- •Приложение 5. Критические значения χ2
- •Приложение 6. Критические значения коэффициента корреляции рангов Спирмена
- •Приложение 7. Критические значения Fкритерия Фишера
- •Ответы к контрольным заданиям
Параметрические критерии проверки статистических гипотез
Наиболее распространенным параметрическим критерием является критерий t-Стъюдента. Его используют для проверки гипотезы о равенстве двух генеральных средних. Как видно из рисунка 18, две выборки могут быть извлечены из одной генеральной совокупности и в этом случае у выборочных средних одна общая генеральная средняя, или же эти выборки принадлежат разным совокупностям и, следовательно, генеральные средние отличаются.
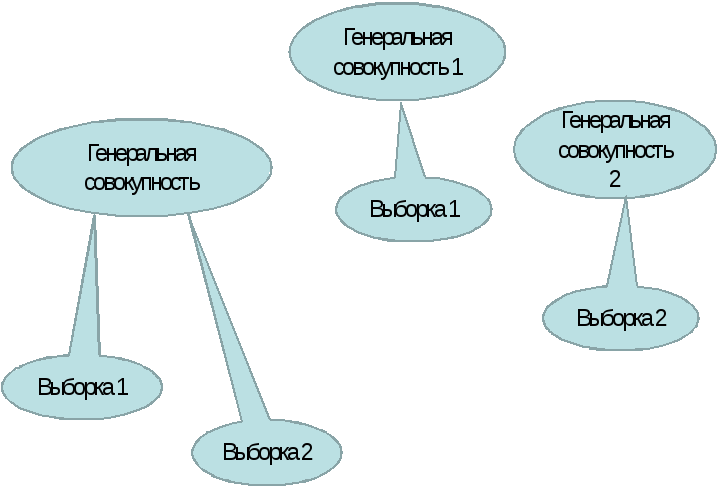
Рисунок 18. Гипотезы о равенстве
Критерий Стъюдента можно использовать при условии, если
признаки количественные и имеют нормальное распределение
генеральные дисперсии сравниваемых совокупностей равны
Несоблюдение этих условий может привести к некорректным результатам.
СЛУЧАЙ 1. Выборки независимые.
В этом случае нулевая гипотеза Н(0) звучит так:
две генеральные средние равны
или - две выборки извлечены из одной генеральной совокупности
или - две совокупности имеют одинаковое распределение
В медицинских задачах гипотеза может быть сформулирована, например, таким образом: содержание гемоглобина у городских и сельских жителей одинаково (подразумевая, что одинаково его распределение).
Проверяемый t-критерий вычисляется по формуле
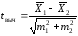 (11)
(11)
где
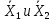 – выборочные средние
– выборочные средние
m1, m2 - стандартные ошибки средних значений сравниваемых выборок.
Находим по таблице tкрит для заданного α и числа степеней свободы
f =n1 + n2 – 2 (12)
Если │tвыч │< tкрит то принимается Н(0) (нет аргументов, чтобы ее отвергнуть)
Если │ tвыч│≥ tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости.
Условие равенства двух генеральных дисперсий проверяется по критерию Фишера, который равен отношению большей выборочной дисперсии к меньшей:
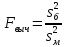 (13)
(13)
Fкрит находится по таблице (Приложение 7) для заданного α и числа степеней свободы
f1=n1-1 и f2=n2-1 (14)
Если Fвыч≥ Fкрит , то гипотеза о равенстве генеральных дисперсий отвергается
Если Fвыч< Fкрит , то принимается нулевая гипотеза о равенстве.
|
Пример. По данным из таблицы 14 определить, отличается ли при себорее содержание связанного холестерина крови (мг%) от нормы, если известно, что концентрация холестерина имеет нормальное распределение, а дисперсии в двух совокупностях одинаковы. Таблица 14. Данные к примеру
Решение: Вычислим средние значения для двух выборок:
Несмотря на то, что две выборочные средние отличаются, не исключена возможность, что генеральные средние равны. Поэтому выдвинем гипотезы: Н(0): среднее значение связанного холестерина в крови при себорее не отличается от нормы Н(1): среднее значение связанного холестерина в крови при себорее отличается от нормы Гипотезы будем проверять на уровне значимости α=0,05. Результаты вычислений представлены в таблице 15.
Таблица15. Итоги проверки гипотезы
Определим Fкрит по таблице (Приложение 7) для f1=8 и f2=7 Fкрит=3,73 Т.к. Fвыч< Fкрит (1,08<3,73) принимаем гипотезу о равенстве генеральных дисперсий Определим tкрит для α=0,05 и числа степеней свободы в двух группах f=n1+n2-2=9+8-2=15 Из таблицы (Приложение 2) получаем двусторонний tкрит=2,13 т.к.│tвыч│> tкрит (20,8>2,13) – то принимается альтернативная гипотеза. Вывод: Содержание связанного холестерина в крови при себорреи статистически значимо отличается от нормы с вероятностью не менее 95%. |
СЛУЧАЙ 2. Выборки зависимые
Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения, и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю изменений этого признака в результате получения терапии.
При подобных исследованиях все наблюдения можно представить в виде n-пар измерений (например, до и после)
Для каждой пары вычисляется разность di, где i=1, n
Для полученного
ряда вычисляется среднее
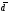 и
среднеквадратичное
отклонение
и
среднеквадратичное
отклонение
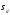
Далее вычисляется значение критерия Стъюдента
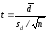 (15)
(15)
Проверка гипотезы производится по таблицам распределения Стьюдента (Приложение 2) для выбранного уровня значимости и числа степеней свободы f= п-1.
Если │tвыч │< tкрит то принимается Н(0)
Если │ tвыч│≥ tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями «до» и «после».
|
Пример. В группе из 6 человек изучалось влияние пробежки на ЧСС (уд/мин). В результате опыта получилось 2 ряда ЧСС: первый – до пробежки, второй – после пробежки: Таблица 16. ЧСС до и после пробежки
Изменяется ли ЧСС после пробежки? Необходимо оценить статистическую значимость полученных результаты, если известно, что ЧСС имеет нормальное распределение. Для наглядности представим данные в следующей таблице 17:
Таблица 17. Изменения ЧСС
x1i (до пробежки) х2i(после пробежки) di(разница ЧСС) 65 77 12 75 82 7 68 65
3 80 90 10 75 85 10 62 75 13 Ср. знач.=70,8 Ср. знач.=79 Ср. знач.= 8,2
Несмотря на то, что средние значения ЧСС до и после пробежки отличаются, не исключена возможность, что в генеральной совокупности пробежка не повлияет на ЧСС. Поэтому выдвигаем гипотезы: Н(0): после пробежки ЧСС в среднем не меняется Н(1): после пробежки ЧСС в среднем меняется Гипотезы будем проверять на уровне значимости α=0,05. Результаты вычислений представлены в таблице 18.
Таблица 18. Результаты проверки гипотезы
Определим по таблице Стьюдента (Приложение 2) для α=0,05 и числа степеней свободы f=n-1=5 двусторонний tкрит = 2,57. │tвыч │> tкрит – следовательно принимается Н(1). Вывод: изменение ЧСС после пробежки статистически значимо с вероятностью не менее 95%. |
Контрольное задание 5:
На каком уровне значимости можно утверждать, что содержание сахара в крови лиц основной и контрольной групп одинаково
Таблица 19. Данные к заданию
|
Сахар в крови, г/л |
|
t0,05 |
t0,01 |
tвыч |
|
Основная группа |
2,262 |
3,25 |
3,11 | |
|
Контрольная группа |
По данным из таблицы 20 сформулируйте нулевую и альтернативную гипотезы. Какая из гипотез будет принята.
Таблица 20. Данные к заданию
|
Аплитуда ЭЭГ |
фон |
альфа |
р |
|
гипервентилляция |
0,05 |
7,5% |

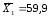
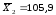
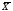 (мг%)
(мг%)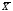 (уд/мин)
(уд/мин)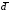 (уд/мин)
(уд/мин)