
- •Оглавление
- •Условные обозначения
- •Предисловие
- •Задачи биостатистики
- •Основные понятия и определения биостатистики
- •Классификация признаков
- •Анализ медико-биологических данных на основе их графического представления
- •Анализ медико-биологических данных на основе числовых статистических характеристик
- •Свойства нормального распределения
- •Теория проверки статистических гипотез
- •I алгоритм
- •II алгоритм
- •Проверка гипотезы о нормальности распределения случайной величины
- •Параметрические критерии проверки статистических гипотез
- •Анализ относительных величин
- •Доверительный интервал
- •Доверительный интервал для разности генеральных средних двух независимых групп
- •Доверительный интервал для разности генеральных средних двух зависимых групп
- •Доверительный интервал относительных показателей
- •Непараметрические критерии проверки статистических гипотез
- •Анализ качественных признаков. Таблицы сопряженности
- •Оценка факторов риска
- •Оценка чувствительности и специфичности диагностических тестов
- •Оценка прогностического значения диагностических тестов
- •Однофакторный дисперсионный анализ
- •Линейная корреляция
- •Коэффициент корреляции рангов к. Спирмена
- •Линейная регрессия
- •Анализ выживаемости
- •Методы прогнозирования
- •Методы простой экстраполяции
- •Метод среднего абсолютного прироста
- •Метод среднего темпа роста
- •Прогнозирование на основе математических моделей
- •Оценка факторов риска и прогнозирование на основе логистической регрессии
- •Анализ качественных признаков на основе логлинейной модели
- •Байесовский подход к диагностике и прогнозированию. Последовательный анализ вальда
- •Определение размера выборки
- •Расчет объема выборки при эпидемиологических исследованиях
- •Представление статистических данных в научных публикациях
- •Заключение
- •Список литературы
- •Приложение 1. Критические значения коэффициента асимметрии As
- •Приложение 2. Критические точки двустороннего tкритерия Стьюдента
- •Приложение 3. Критические значения Uкритерия МаннаУитни
- •Приложение 4. Критические значения парного Ткритерия Уилкоксона
- •Приложение 5. Критические значения χ2
- •Приложение 6. Критические значения коэффициента корреляции рангов Спирмена
- •Приложение 7. Критические значения Fкритерия Фишера
- •Ответы к контрольным заданиям
Доверительный интервал
Любая выборка дает лишь приближенное представление о генеральной совокупности, и все выборочные статистические характеристики (средняя, мода, дисперсия…) являются некоторым приближением или говорят оценкой генеральных параметров, которые вычислить в большинстве случаев не представляется возможным из-за недоступности генеральной совокупности (Рисунок 20).
Рисунок
20. Ошибка выборки
Но можно указать интервал, в котором с определенной долей вероятности лежит истинное (генеральное) значение статистической характеристики. Этот интервал называется доверительный интервал (ДИ).
Так генеральное среднее значение с вероятностью 95% лежит в пределах
от
 до
до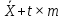 ,
(20)
,
(20)
где t – табличное значение критерия Стъюдента для α=0,05 и f=n-1
Может быть найден и 99% ДИ, в этом случае t выбирается для α=0,01.
Какое практическое значение имеет доверительный интервал?
Широкий доверительный интервал показывает, что выборочная средняя неточно отражает генеральную среднюю. Обычно это связано с недостаточным объемом выборки, или же с ее неоднородностью, т.е. большой дисперсией. И то и другое дают большую ошибку среднего и, соответственно, более широкий ДИ. И это является основанием вернуться на этап планирования исследования.
Верхние и нижние пределы ДИ дают оценку, будут ли результаты клинически значимы
Остановимся несколько подробнее на вопросе о статистической и клинической значимости результатов исследования групповых свойств. Вспомним, что задачей статистики является обнаружение хоть каких-либо отличий в генеральных совокупностях, опираясь на выборочные данные. Задачей клиницистов является обнаружение таких (не любых) различий, которые помогут диагностике или лечению. И не всегда статистические выводы являются основанием для клинических выводов. Так, статистически значимое снижение гемоглобина на 3 г/л не является поводом для беспокойства. И, наоборот, если какая-то проблема в организме человека не имеет массового характера на уровне всей популяции, это не основание для того, чтобы этой проблемой не заниматься.
|
Это положение рассмотрим на примере. Исследователи задались вопросом, не отстают ли в росте от своих сверстников мальчики, перенесшие некое инфекционное заболевание. С этой целью было проведено выборочное исследование, в котором приняли участие 10 мальчиков, перенесших эту болезнь. Результаты представлены в таблице 23.
Таблица 23. Результаты статобработки
Из этих расчетов следует, что выборочный средний рост мальчиков 10 лет, перенесших некое инфекционное заболевание, близок к норме (132,5 см). Однако нижний предел доверительного интервала (126,6 см) свидетельствует о наличии 95% вероятности того, что истинный средний рост этих детей соответствует понятию «низкий рост», т.е. эти дети отстают в росте. В этом примере результаты расчетов доверительного интервала клинически значимы. | |||||||||||||||||||

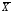 (см)
(см)