3. Описание состояний. Волновая функция. Принцип суперпозиции

Как описываются волновые частицы и системы таких частиц?

Постулат 0. Все свойства чистого1состояния квантовой системы описываются волновой функцией (амплитудой вероятности)

Под волновой функцией или амплитудой вероятности понимают комплексную функцию действительных переменных (,t), где– набор переменных системы, аt– момент времени. В координатном представлении подпонимают совокупность координат частиц системы:

 = (x₁, y₁, z₁, x₂, y₂, z₂, ... ).

Квадрат модуля волновой функции определяет плотность распределения переменных(М. Борн, 1926 г.):

(, t) = |(, t)|² = ^*(, t) (, t). (3.1)

Вероятность того, что в момент tзначения координат частиц лежат в интервале (,+d) будет равна

dw(, t) = (, t)d. (3.2)

Умножение волновой функции на число не приводит к новому состоянию. Поэтому ее принято нормировать так, чтобы полная вероятность была равна единице:

_ |(,t)|²d= 1. (3.3)

Интегрирование здесь производится по всей области возможных значений переменных . Следовательно, волновая функция должна быть квадратично интегрируемой. (Множество всех квадратично интегрируемых комплексных функций действительных переменных называют гильбертовым пространством и обозначаютL₂. Поэтому волновые функции представляют собой элементы гильбертова пространства).

Из статистического смысла волновой функции (1) следует, что и нормированная волновая функция остается неоднозначной. Она определяется с точностью до фазового множителя e^i, где– любое действительной число. Если произвести замену(,t)e^i(,t), то это не отразится на значениях измеряемых в опыте величин. Ведь в опыте можно измерить плотность вероятности, но не волновую функцию.

Анализ результатов многих экспериментов с микрочастицами показывает, что для состояний квантовых систем справедлив еще один фундаментальный принцип – принцип суперпозиции:

Если система может находиться в состояниях, описываемых волновыми функциями₁и₂,то она может находиться и в состоянии

=a₁₁+a₂₂, (3.4)

гдеa₁иa₂–произвольные комплексные числа, не нарушающие нормировку.

Например, рассмотренный выше опыт по интерференции можно объяснить, если значения волновой функции в точках наблюдения можно представить в виде линейной комбинации (4). Только в этом случае распределение вероятности попадания частиц в различные участки экрана будет содержать интерференционные члены:

||² = |a₁|²|₁|² + |a₂|²|₂|² + a₁*a₂₁*₂, + a₁a₂*₁₂*.

Математическим следствием принципа суперпозиции являетсялинейностьуравнений, которым удовлетворяют волновые функции.

Система постулатов квантовой механики должна быть построена таким образом, чтобы сами постулаты и выводы из них удовлетворяли сформулированным выше фундаментальным принципам, в которых сконцентрированы данные опыта. Помимо рассмотренных принципов: квантования, неопределенностей и суперпозиции далее будут рассмотрены также принцип причинности и принцип тождественности частиц.

4. Описание наблюдаемых. Эрмитовы операторы. Собственные функции и собственные значения операторов

Состояния квантовой системы характеризуются волновыми функциями, значения которых не могут быть измерены в опыте. В этом смысле состояния системы не наблюдаемы. Всякая теория должна рассматривать величины, значения которых могут измеряться в опытах, хотя бы в принципе. В квантовой механике их называют наблюдаемыми. Их значения должны быть действительными.

Постулат 1. Каждой наблюдаемойFставится в соответствие линейный эрмитов оператор.

Постулат 2. НаблюдаемаяFв любом квантово-механическом состоянии может принимать только те значения, которые являются собственными значениями ее оператора.

Рассмотрим некоторые необходимые математические определения, относящиеся к операторам.

1. Операторомназывают правило, которое функции() ставит в соответствие функцию():() =(). Примеры: операторы умножения на число, возведения в степень, умножения на некоторую функцию, однократного и многократного дифференцирования и т.д.

2. Оператор называютединичным, если для любой функции() имеет место() =().

3. Суммойилиразностью() операторовиназывают оператор, для которого имеет место ()=. Очевидна коммутативность и ассоциативность суммы операторов:,.

4. Умножение оператора на числоэквивалентно умножению на это число результата действия оператора: (a)=a().

5. Оператор называютлинейным, если для любых функций() и() имеет место(a+b) =a+b, гдеaиb– любые комплексные числа. Например, операторы умножения на функцию или число, операторы дифференцирования являются линейными, а операторы возведения в квадрат или в куб, операторы логарифмирования – нелинейными.

6. Произведениемоператоровназывают оператор, действие которого на функцию сводится к последовательному применению сначала оператора, а затем:. Произведение операторов обладает свойством ассоциативности и дистрибутивности:,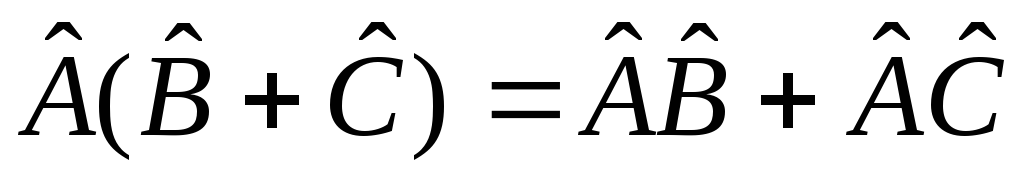. В общем случае произведение операторов не коммутативно:.

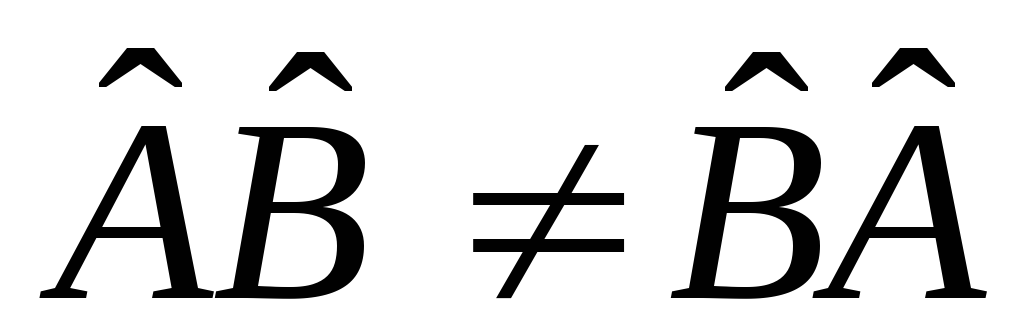7. Коммутаторомоператоровиназывают их перестановочное соотношение, обозначаемое так:. Если операторыикоммутируют, то. Легко видеть, что.

8. Оператор ^–1, удовлетворяющий условию, называют обратным оператору, если он существует.

9. Оператор называют эрмитовым (самосопряженным), если для произвольных функций₁^*и₂имеет место_₁^*₂d=_₂^*₁^*d.

10. Уравнение вида =A, гдеA– число,– искомая функция, называютуравнением на собственные функцииоператора. В общем случае решения этого уравнения существуют только для определенных значенийA_n, называемыхсобственными значениямиоператора:_n=A_n_n, где_n– соответствующие собственные функции.

11. Собственное значение называют невырожденным, когда ему соответствует (с точностью до постоянного множителя) лишь одна собственная функция. В противном случае собственные значения называютвырожденными(двукратно, трехкратно и т.д.). Совокупность собственных значений {A_n} называютспектромоператора. Спектры операторов могут быть дискретными, непрерывными или смешанными. Для определенности в дальнейшем будем рассматривать преимущественно операторы с дискретным спектром.

Физический смысл постулатов 1 и 2 помогают раскрыть следующие теоремы.

Теорема 1. Собственные значения линейных эрмитовых операторов являются действительными.

Доказательство. Пусть – линейный эрмитов оператор, собственные функции которого удовлетворяют уравнению

=F. (4.1)

Сопряженное ему уравнение имеет вид

** =F**. (4.2)

Умножив слева первое уравнение на *, а второе – на, проинтегрируем обе части каждого по всем возможным значениям переменных и вычтем почленно одно из другого. Оператор – эрмитов, поэтому

0 = (F–F*)_^*d. (4.3)

Так как _^*d> 0, получаемF=F*. Следовательно,F– действительное.

Определение. Говорят, что функции() и() взаимноортогональны, если

_^*()()d= 0. (4.4)

Теорема 2. Собственные функции линейного эрмитова оператора, относящиеся к различным собственным значениям, ортогональны.

Доказательство. Пусть_nи_m– собственные функции линейного эрмитова оператора , относящиеся к различным собственным значениям:

_n = F_n_n, (4.5)

*_m* = F_m_m*. (4.6)

Умножив слева первое уравнение на _m*, а второе – на_n, проинтегрируем обе части каждого по всем возможным значениям переменных и вычтем почленно одно уравнение из другого. Оператор – эрмитов, поэтому

0 = (F_n–F_m)__m*_nd. (4.7)

Так как по условию F_nF_m, получаем условие ортогональности:

__m*_nd= 0. (4.8)

Объединив условие ортогональности (4.8) собственных функций с условием нормировки (3.3), получаем условие, называемое условием ортонормированностисобственных функций оператора наблюдаемой:

__m*_nd=_mn, (4.9)

где _mn– дельта-символ Кронекера,

_mn=. (4.10)

Еще одним важным свойством оператора наблюдаемой является полнотасистемы его собственных функций, которая выражается условием

_n*() =(–), (4.11)

где (–) – дельта-функция Дирака. По сути, условие полноты и является необходимым условием того, что соответствующий эрмитов оператор представляет наблюдаемую величину.