Свой­ства квад­ра­тич­ной функ­ции

Здесь рас­смат­ри­ва­ют­ся свой­ства квад­ра­тич­ной функ­ции вида ,гра­фик квад­ра­тич­ной функ­ции и ре­ша­ют­ся за­да­чи на чте­ние гра­фи­ков и за­да­чи с па­ра­мет­ром. 

Напоминание

Опре­де­ле­ние. Квад­ра­тич­ной функ­ци­ей на­зы­ва­ет­ся функ­ция вида

, где .

Гра­фик – па­ра­бо­ла (см. Рис. 1) с вер­ши­ной в точке , где.

 

Рис. 1. Гра­фик функ­ции , где

. Функ­ция непре­рыв­на на всей .

  Свойства функции

  в слу­чае .

Пусть .

Свой­ства:

1. ;

2. ;

3. убы­ва­ет при;воз­рас­та­ет при;

4. - не су­ще­ству­ет;

5. Непре­рыв­на;

6. Вы­пук­ла вниз.

  Свойства функции

  в слу­чае .

Пусть .

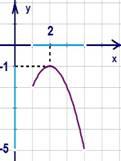
Свой­ства (см. Рис. 2):

 

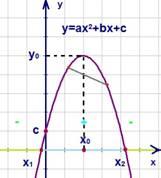
Рис. 2. Гра­фик функ­ции в слу­чае.

1. ;

2. ;

3. воз­рас­та­ет при;убы­ва­ет при;

4. - не су­ще­ству­ет;

5. Непре­рыв­на;

6. Вы­пук­ла вверх.

 Задача 1 на нахождение пределов изменения конкретной квадратичной функции

Най­ди­те пре­де­лы из­ме­не­ния функ­ции, про­чи­тай­те гра­фик.

 

а. 

Ответ: ;убы­ва­ет при;воз­рас­та­ет при.

	б.

Ответ: ;убы­ва­ет при;воз­рас­та­ет при.

Задача 2 на нахождение пределов изменения конкретной квадратичной функции

Най­ди­те пре­де­лы из­ме­не­ния функ­ции, про­чи­тай­те гра­фик.

	а.

Ответ: ;воз­рас­та­ет при;убы­ва­ет при.

 

б. 

Ответ: ;воз­рас­та­ет при;убы­ва­ет при.

  Задача 1 с параметром

Най­ди­те число кор­ней урав­не­ния с па­ра­мет­ром, где,.

Ответ (см. Рис. 3):

 

Рис. 3. Гра­фик функ­ции , рас­се­чен­ный пря­мы­ми, гдеи.

1. Кор­ней нет при ;

2. Урав­не­ние имеет

- один ко­рень при ;

- два корня при .

Задача 2 с параметром

Най­ди­те все зна­че­ния па­ра­мет­ра , при каж­дом из ко­то­рых урав­не­ние, где,, имеет хотя бы один ко­рень (см. Рис. 4).

 

 

 

 

 Ответ: .

Задача на построение и чтение графика функции

По­строй­те и про­чи­тай­те гра­фик функ­ции

 

, 

Ответ: (см. Рис. 5)

 

Рис. 5. Гра­фик функ­ции 

1. Воз­рас­та­ет при ;

2. Убы­ва­ет при .

Задача 3 с параметром

Най­ди­те число кор­ней урав­не­ния , где.

Ответ: урав­не­ние имеет (см. Рис. 6)

 

Рис. 6. Гра­фик функ­ции  ,

рас­се­чен­ный пря­мы­ми , гдеи.

1. Один ко­рень при ;

2. Два корня при ;

3. Три корня при .

 

За­да­чи на сте­пен­ные функ­ции

Здесь вспомним свой­ства сте­пен­ных функ­ций с целым от­ри­ца­тель­ным по­ка­за­те­лем и ис­поль­зу­ем их при ре­ше­нии задач на сте­пен­ную функ­цию.

  Напоминание: график и свойства функции

Функ­ция 

Ос­нов­ные свой­ства:

1. 

2. 

3. Функ­ция чет­ная.

4. Две ха­рак­тер­ные фик­си­ро­ван­ные точки для всех кри­вых: 

5. Асимп­то­ты: пря­мые 

6. Если тоy воз­рас­та­ет, 

Если тоy убы­ва­ет, 

  Напоминание: график и свойства функции

Функ­ция 

Ос­нов­ные свой­ства:

1. 

2. 

3. Функ­ция нечет­ная.

4. Две фик­си­ро­ван­ные ха­рак­тер­ные точки для всех кри­вых: 

5. Асимп­то­ты: пря­мые 

6. Если тоy убы­ва­ет, 

Если тоy убы­ва­ет, 

Решение задач

Рас­смот­рим ти­по­вые за­да­чи:

1. Какая из точек – А или В – при­над­ле­жит гра­фи­ку функ­ции если

Ре­ше­ние:

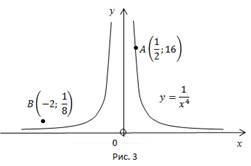
т. А: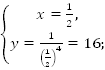 

т. А при­над­ле­жит гра­фи­ку.

т. В: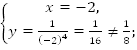 

т. В не при­над­ле­жит гра­фи­ку.

Ответ: т. А.

2. Какая из точек А, В, С при­над­ле­жит гра­фи­ку функ­ции если

 

Ре­ше­ние:

т. А: 

т. В: 

т. С: 

Ответ: т. В при­над­ле­жит гра­фи­ку.

3. По­строй­те гра­фик функ­ции и про­чти­те его.

Ре­ше­ние:

По­стро­им гра­фик функ­ции (Рис. 5). Его асимп­то­ты – пря­мыеи.

 

Чтобы по­лу­чить гра­фик функ­ции необ­хо­ди­мо гра­фиксдви­нуть на 1 вверх по осиyи на 1 еди­ни­цу влево по оси x (Рис. 6).

Асимп­то­ты по­лу­чен­но­го гра­фи­ка – пря­мые и, ха­рак­тер­ные точки

Если тоy воз­рас­та­ет, 

Если тоy убы­ва­ет, 

4. Най­ди­те все зна­че­ния па­ра­мет­ра m, при каж­дом из ко­то­рых урав­не­ние

 имеет хотя бы одно ре­ше­ние.

Ре­ше­ние:

Нам необ­хо­ди­мо по­стро­ить гра­фик функ­ции , пе­ре­сечь его се­мей­ством пря­мых, найти точки пе­ре­се­че­ния и за­пи­сать ответ (Рис. 7).

Ответ: 

5. Найти все зна­че­ния па­ра­мет­ра m, при каж­дом из ко­то­рых урав­не­ние  

1. Не имеет ре­ше­ний.

2. Имеет толь­ко от­ри­ца­тель­ные ре­ше­ния.

3. Имеет два корня раз­ных зна­ков.

Ре­ше­ние:

Ответ:

1. 

2. 

3. 

6. По­строй­те гра­фик функ­ции и про­чи­тай­те его.

Ре­ше­ние:

По­стро­им гра­фик функ­ции (Рис. 8).

Те­перь чтобы по­лу­чить гра­фик функ­ции сдви­нем кри­вуюна 2 впра­во вдоль осиx, и на 3 вверх по осиy (Рис. 9).

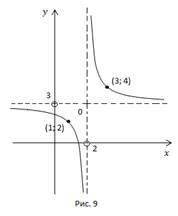
Пря­мые ияв­ля­ют­ся асимп­то­та­ми.

Ха­рак­тер­ные точки – 

Если тоy убы­ва­ет, 

Если тоy убы­ва­ет, 

7. Найти все зна­че­ния па­ра­мет­ра m, при каж­дом из ко­то­рых урав­не­ние

 имеет ре­ше­ния

1. На луче 

2. На луче 

Ре­ше­ние:

Изоб­ра­зим гра­фик функ­ции и пе­ре­се­чем его се­мей­ством пря­мых(Рис. 10).

Ответ:

1. 

2. 

8. Ре­ши­те гра­фи­че­ски нера­вен­ство 

Ре­ше­ние:

По­стро­им в одной си­сте­ме ко­ор­ди­нат гра­фик функ­ции и гра­фик функ­ции(Рис. 11).

Гра­фи­ки пе­ре­се­ка­ют­ся в точке 

 

Чтобы вы­пол­ня­лось нера­вен­ство кри­ваядолж­на рас­по­ла­гать­ся выше пря­мой

Ответ: 

9. Даны две функ­ции, и, где

До­ка­жи­те, что 

До­ка­за­тель­ство:

 

 

 

Тож­де­ство до­ка­за­но.