3. Изучение свойств функции
Рассмотрим
функцию 
Например,
Это четная функция. Графики всех таких функций проходят через три фиксированные точки (0; 0); (1; 1); (-1; 1).
Кривая 
касается
осиx в
точке (0; 0) и похожа на кривую 
но
круче при
Рассмотрим
взаимное расположение
кривых 
|
|
0 |
|
2 |
|
|
0 |
|
4 |
|
|
0 |
|
6 |
4. Решение задач
Рассмотрим примеры.
1.
Что больше: 
Ответ:
Что
больше: 
Ответ:
Что
больше: 
Ответ:
2.
Построить графики функций
и найти 
:
a. 
b. 
Решение:
a.
Чтобы получить график
функции 
необходимо
построить график функции
и сдвинуть его на 2 вправо вдоль
осиx (Рис.
4).
b.
Чтобы получить график
функции 
необходимо
построить график функции
и
сдвинуть его на 1 вверх вдоль осиy (Рис.
5).
3.
Найти 
построить
график функции
Решение:
Чтобы получить график функции 
,
кривую
необходимо
сдвинуть на 1 вправо и на 0,5 вверх
(Рис. 6).
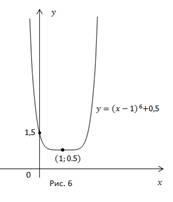
В следующей задаче мы используем данные предыдущей задачи.
4. Найти все значения параметра a, при каждом из которых уравнение
имеет
хотя бы одно решение.
Решение:
Рассмотрим
построенный график
функции 
(Рис.
6) и пересечем его семейством
прямых
.
Если 
нет
решений.
Если 
1
решение.
Если 
2
решения.
Фактически, множеством значений параметра, при которых уравнение имеет решение, является множество значений функции
Ответ: 
5.
Найти все значения параметра 
,
при каждом из которых уравнение
имеет:
a. два корня разных знаков;
b. два положительных корня.
Решение:
Методика
та же, что и в предыдущей задаче
– рассмотреть график функции 
и
пересечь его семейством
прямых
(Рис.
6).
Ответ:
a. 
b. 
Определить
число решений системы 
Решение:
Построим
графики функций 
и
в
одной системе координат
(Рис. 7).
На
промежутке 
функция
убывает,
а функция
возрастает,
имеется одна точка пересечения.
На промежутке
функция
возрастает,
а функция
убывает,
имеется одна точка пересечения.
Итого, имеется два решения
данной системы.
Ответ: Два решения.
Исследование функций на четность
В этой лекции напомним определения и свойства четных и нечетных функций, сформулируем алгоритм исследования функций на четность, и рассмотрим пример использования алгоритма для решения конкретных задач.
Напоминание:
Функция 
называется
четной, если для любого
График четной функции симметричен относительно оси y. Верно и обратное – если график функции симметричен относительно оси y, то функция четная.
Функция 
называется
нечетной, если для любого
График нечетной функции симметричен относительно начала координат. Верно и обратное – если график функции симметричен относительно начала координат, то функция нечетна.
Приведенные факты сформулируем более кратко и проиллюстрируем на графике.
1.
(Рис
).
2.
(Рис.
2).
Этими опорными фактами мы будем пользоваться при определении четности функции.
Алгоритм исследования функции на четность
Из приведенных определений и свойств вытекает
Алгоритм
исследования функции 
на
четность.
1.
Исследовать 
на
симметричность относительно
нуля
Если
не
симметрична относительно
нуля, это функция общего вида.
2.
Найти 
3.
Сравнить 
-
если 
то
функция четная;
-
если 
то
функция нечетная;
-
если хотя бы для одного 
то
это функция общего вида.
Решение примеров
Рассмотрим конкретные примеры.
Исследовать функцию на четность:
1. 
Решение:
(Рис.
3).
Область определения состоит из всех действительных чисел, кроме нуля. Область определения симметрична относительно нуля.
Ответ: Функция четная.
2. 
.
Решение:
(Рис.
4).
несимметрична
относительно нуля, значит
это функция общего вида.
Ответ: Функция общего вида.
3. 
Решение:
область
определения симметрична
относительно нуля.
Ответ: Функция нечетная.
4. 
Решение: 
(Рис.
5).
Область определения симметрична относительно нуля.
Ответ: Функция нечетная.
5. 
Решение: 
Область определения симметрична относительно нуля (Рис. 5).
Ответ: Функция четная.
6. 
Решение: 
Область
определения симметрична
относительно нуля.
Мы
видим, что для 
:
Функция
не является ни четной, ни
нечетной, значит, это функция
общего вида
Ответ: Функция общего вида.
7.
.
Решение: 
(Рис.
6).
Область определения несимметрична относительно нуля.
Ответ: Функция общего вида.
8. 
Решение:
Построим график функции (Рис. 7).
График симметричен относительно оси y, функция четная.
Эту
же функцию можно задать как 
Ответ: Функция четная.
9.
Постройте график функции 
и
прочитайте его, если
Решение: Построим график функции (Рис. 8).
График симметричен относительно оси y, функция четная.
Функция
возрастает при 
Функция
убывает при 