3. Понятие «устойчивость системы управления»

Система является устойчивой, если при любом ограниченном входном сигнале выходной сигнал также является ограниченным во все моменты времени. Таким образом, устойчивость системы гарантирует, что система не «пойдет вразнос». При этом не важно, как меняются внутренние переменные объекта, важны только входная и выходная переменные.

В классической теории устойчивости исследуется не устойчивость системы как таковой, а устойчивость ее так называемого невозмущенного движения, т.е. свободного движение системы без внешнего воздействия. Тогда под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Положением равновесия называют состояние системы, которая находится в покое, т.е. выходной сигнал — постоянная величина, и все его производные равны нулю.Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой (рис. 4.1).

Рис. 4.1. Устойчивость систем

Система автоматического управления может быть неустойчивой по двум причинам: неподходящий состав динамических звеньев и неподходящие значения параметров звеньев. Системы, неустойчивые по первой причине называются структурно неустойчивыми. Это означает, что изменением параметров системы управления нельзя добиться ее устойчивости, нужно менять ее структуру, например, с помощью местных обратных связей или включить в систему корректирующие звенья.

Правила, позволяющие судить об устойчивости системы, называются критериями устойчивости. Их можно разделить на алгебраические и частотные.

5. Условие устойчивости систем по а.М. Ляпунову и корневой критерий устойчивости

Решение дифференциального уравнения ищется в виде:

.

Здесь — решение однородного дифференциального уравнения, т.е. уравнения с нулевой правой частью:

.

  Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения.

—частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие . Поэтому вторая составляющая общего решения называетсявынужденной. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

Свободная составляющая представляет собой сумму из отдельных составляющих:, где— корни характеристического уравнения.

Корни могут быть либо вещественными, либо комплексно сопряженными . Постоянные интегрирования определяются исходя из начальных условий, подставляя в общее решение значенияи их производные в моменты времени и .

Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая , каждому положительному — экспоненциально расходящаяся, каждому нулевому корню соответствует (рис. 4.2).

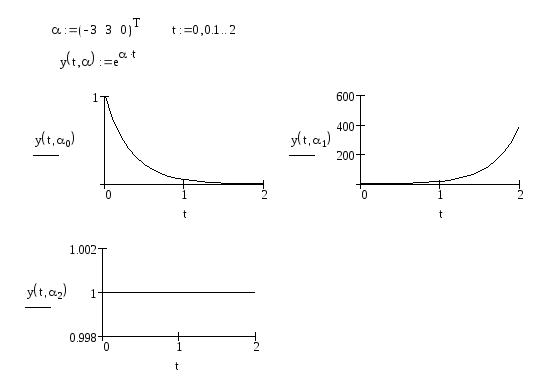
Рис. 4.2. Вид свободного решения уравнения при действительных корнях (фрагмент документа пакета Mathcad)

Пара комплексно-сопряженных корней с отрицательной вещественной частью определяет затухающие колебания, при положительной вещественной части — расходящиеся колебания, при нулевой — незатухающие (рис 4.3).

Так как после снятия возмущения , то устойчивость системы определяется только характером свободной составляющей . Поэтому условие устойчивости систем по А.М. Ляпунову формулируется так [5, 10]: в устойчивой системе свободная составляющая решения уравнения динамики, должна стремиться к нулю, т.е. затухать.

Тогда корневой критерий устойчивости: для того чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения (знаменателя передаточной функции замкнутой системы) имели отрицательные вещественные части (на комплексной плоскости были левыми). Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю, а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно-сопряженных корней, то система находится на границе колебательной устойчивости.

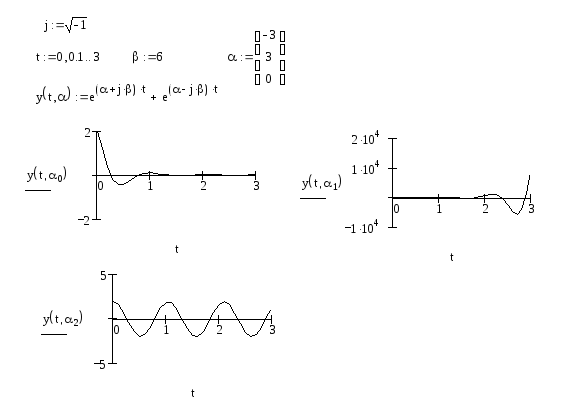
Рис. 4.3. Вид свободного решения уравнения при комплексно-сопряженных корнях (фрагмент документа пакета Mathcad)

Необходимое условие устойчивости. Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде:

,

(4.1)

где — корни уравнения.

Если система устойчива, значит все корни левые, т.е. вещественные части всех корней отрицательны, что можно записать как . Подставим их в уравнение:

.

Перемножая комплексно-сопряженные выражения, получим:

.

После раскрытия скобок получится выражение:

.

Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов не будет отрицательным. Поэтомунеобходимым условием устойчивости системы автоматического управления является положительность всех коэффициентов характеристического уравнения: [12].

Для систем первого и второго порядков это условие одновре­менно является и достаточным. Однако для более высоких порядков поло­жительность коэффициентов не гарантирует отрицательность корней характеристического уравнения.