
Лабораторная работа3
.docЛабораторная работа № 3
Цель лабораторной работы заключается в изучении и приобретении навыков работы в электронной таблице Excel с логическими функциями и построения разветвляющихся алгоритмов для решения задач
Основными задачами, решаемыми в процессе выполнения лабораторной работы, являются:
-
Разработка алгоритмов и их реализация на Excel и VBA.
-
Ознакомление с логическими функциями.
-
Приобретение практических навыков работы с процедурами –обработчиками событий.
Задание 1.
Рассчитать значение функции z=f(x,y), учитывая область существования. Считать, что аргументы x и y изменяются одновременно, принимая не менее 10 пар значений. Начальные, конечные значения и шаги изменения аргументов x и y задать самостоятельно. В том случае, если функция z не существует, выдать в качестве результата «Функция не существует» .
1.
z=ln(x+y) 13. z=![]()
2.
z=sin![]() 14. z=
14. z=![]()
3. z=lnx+lny 15. z=lnx+9y
4.
z=![]() 16. z=
16. z=![]()
5.
z=ln(xy) 17. z=![]()
6.
z=tg![]() 18. z=
18. z=![]()
7. z=lnx-4lny 19. z=y+lnx
8.
z=![]() 20. z=
20. z=![]()
9.
z=![]() 21. z=sin
21. z=sin![]()
10.
z=ln(x![]() y)
22. z=
y)
22. z=![]()
11.
z=ctg![]() 23. z=
23. z=![]() +lny
+lny
12. z=lnx+lnxy 24. z=lnxy+lny
25.
z=![]() 26. z=
26. z=![]()
27.
z=cos![]() 28. z=
28. z=![]()
29.
z=![]() 30. z=
30. z=![]()
Задание 2:
Заданы числа х и у и область D. Рассчитать величину z по формуле:
1 .
1
.
1
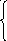 (x
(x![]() +1)
+1)![]() ,
(x,y)
D
,
(x,y)
D


 -1
1 z=
-1
1 z=
y![]() -1)
-1)![]() ,
(x,y) D
,
(x,y) D
 -1
-1
2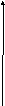 .
.

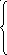 1
1



![]() ,
(x,y)
D
,
(x,y)
D
z=
-1 1 1+y, (x,y) D
-1
3. 1
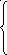

![]() ,
(x,y)
D
,
(x,y)
D
z=


 1
1
![]() ,
(x,y) D
,
(x,y) D
 -1
-1
4 .
.
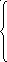 1
1

 x
x![]() ,
(x,y)
D
,
(x,y)
D

-1 1 z=

 15
, (x,y) D
15
, (x,y) D
 -1
-1
5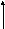 .
1
.
1


-1
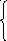



 1
e
1
e![]() ,
(x,y)
D
,
(x,y)
D
z=
y , (x,y) D
 -1
-1
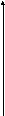
1


x![]() +4
+4![]() ,
(x,y)
D
,
(x,y)
D

 -1
1 z=
-1
1 z=
1 , (x,y) D
-1
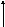

 1
1
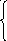
-
cos x +e
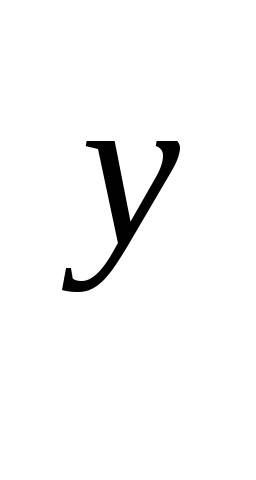 ,
(x,y)
D
,
(x,y)
D


 z=
z=
-1 1 3-x , (x,y) D
-1
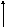
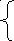 8.
8.
 1
x
1
x![]() -y
, (x,y)
D
-y
, (x,y)
D
z=
2x+1 , (x,y) D


 1
1
 -1
-1
1
9

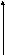 .
.
![]() , (x,y)
D
, (x,y)
D
-1 z=


 1-|x|
, (x,y) D
1-|x|
, (x,y) D

-1


1 0.
1
0.
1
![]() ,
(x,y)
D
,
(x,y)
D


 -1
1 z=
-1
1 z=
![]() , (x,y)
D
, (x,y)
D
 -1
-1
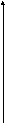
11.
1


e![]() +x
+x![]() sin
y , (x,y)
D
sin
y , (x,y)
D
-1 1 z=


 1
, (x,y) D
1
, (x,y) D
-1

1
 2.
1
2.
1
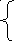
-1
1 x![]() -3y
+ 4xy , (x,y)
D
-3y
+ 4xy , (x,y)
D



 z=
z=
3x-y , (x,y) D
-1
1


 13.
y+
13.
y+
![]() , (x,y)
D
, (x,y)
D
z=
1 2x , (x,y) D


-1

1
1
 4.
4.
2x sin4y , (x,y) D
-1 1 z=

 x
x![]() +y
, (x,y) D
+y
, (x,y) D
-1
 1
1
1 5.
5.

 -1
1
-1
1
![]() , (x,y)
D
, (x,y)
D
z=

![]() -
1 , (x,y) D
-
1 , (x,y) D
- 1
 1
1
1 6.
6.
xcos2y, (x,y) D
z=
-1
1
ln(x![]() +y
+y![]() ),
(x,y) D
),
(x,y) D


-1
1
 7.
1
7.
1

 1
1
![]() , (x,y)
D
, (x,y)
D
z=
![]() ,
(x,y) D
,
(x,y) D
-
1

1 8.
8.
-1
1 ln(x![]() )
, (x,y)
D
)
, (x,y)
D


 z=
z=
![]() ,
(x,y) D
,
(x,y) D
- 1


 1
1
19.

-1
1 e![]() +y,
(x,y)
D
+y,
(x,y)
D

 z=
z=
5xy, (x,y) D
 1
1
2 0.
3xy
0.
3xy![]() ,
(x,y)
D
,
(x,y)
D
z=


 -1
1
-1
1
![]() ,
(x,y) D
,
(x,y) D
-1

2 1.
1
1.
1

![]() ,
(x,y)
D
,
(x,y)
D

 1
z=
1
z=
2, (x,y) D

2 2.
1
2.
1
1
 -
-![]() ,
(x,y)
D
,
(x,y)
D
-1 z=

 1+2׀y׀,
(x,y) D
1+2׀y׀,
(x,y) D
-1

1
2

 4.
4.
y+cos׀x׀, (x,y) D
z=

 2y,
(x,y) D
2y,
(x,y) D
-1 1
-1
2


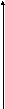 5.
1
5.
1
![]()
![]() -lny,
(x,y)
D
-lny,
(x,y)
D
z=
-1 1 5, (x,y) D


- 1
2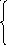

 6.
1
6.
1
![]() , (x,y)
D
, (x,y)
D
z=
-1 1 x, (x,y) D


- 1
2 7.
7.

 1
1
![]() , (x,y)
D
, (x,y)
D
z=


 -1
1
3x, (x,y) D
-1
1
3x, (x,y) D
- 1
2 8.
8.

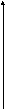 1
1
![]() , (x,y)
D
, (x,y)
D
z=

 1
2(3-y),
(x,y) D
1
2(3-y),
(x,y) D
- 1


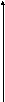 1
1
29.
 e
e![]() , (x,y)
D
, (x,y)
D
z=

 -1
1
1 , (x,y) D
-1
1
1 , (x,y) D
- 1

 1
1
30.
3x![]() +4xy+5y
+4xy+5y![]() , (x,y)
D
, (x,y)
D
z=


 -1
1
8e
-1
1
8e![]() ,
(x,y) D
,
(x,y) D
- 1
Задание 3.
Вычислить функцию y=f(x), обеспечив не менее 4-х точек из каждого интервала:

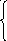
1.
–x![]() +3 , если x-6
2. x
+3 , если x-6
2. x![]() +1
, если x<-1
+1
, если x<-1
y=
x![]() +lnx
, если 0<x2
y=
2x+
+lnx
, если 0<x2
y=
2x+![]() , если 1<x9
, если 1<x9
x![]() +1
, если x>2
x
+1
, если x>2
x![]() +1
, если x>9
+1
, если x>9
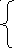
3 .
x
.
x![]() -3 , если x0
4. x
-3 , если x0
4. x![]() +3
, если x0
+3
, если x0
y=
(x+1)![]() , если 0<x8
y=
lnx
, если 0<x
7
, если 0<x8
y=
lnx
, если 0<x
7
3+![]() , если x>12
, если x>12
![]() , если x>10
, если x>10
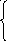
5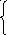 .
sin x
.
sin x![]() , если x-10
6. |x|
-1 , если x-1
, если x-10
6. |x|
-1 , если x-1
y= cos x , если 0<x2 y= x+lnx , если 2<x6
ln
x
, если x>20
2x+e![]() , если x>16
, если x>16
7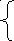
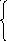 .
cosx
, если x-
8. 2x
+4 , если x3
.
cosx
, если x-
8. 2x
+4 , если x3
y=
tgx
, если <x2
y=
![]() ,
если 3<x6
,
если 3<x6
x+![]() , если x>2
x
, если x>2
x![]() -1
, если x>10
-1
, если x>10
9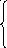
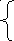 .
x
.
x![]() +sinx
, если x-2
10. e
+sinx
, если x-2
10. e![]() ,
если x0
,
если x0
y=
x+lnx
, если 2<x5
y=
e![]() , если 6<x12
, если 6<x12
e![]() ,
если x>5
sinx
,
если x>5
sinx![]() , если x>12
, если x>12
1
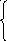 1.
sinx
, если x<0
12 2+ e
1.
sinx
, если x<0
12 2+ e![]() ,
если x-4
,
если x-4
y=
![]() x
, если 6<x10
y=
x+6
, если 2<x4
x
, если 6<x10
y=
x+6
, если 2<x4
lnx , если x>10 ln x , если x>4
1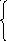
 3.
2x
3.
2x![]() , если x-10
14. 2+sinx
, если x-1
, если x-10
14. 2+sinx
, если x-1
y=
![]() ,
если 0<x5
y=
x+4
, если 4<x5
,
если 0<x5
y=
x+4
, если 4<x5
cos![]() x
x![]() , если x>5
lnx , если x>5
, если x>5
lnx , если x>5

