3.Деление отрезка в данном отношении. Пусть точка c лежит на отрезке ab. Говорим, что c делит отрезок ab в отношении 1:2 , если

₌  ₂AC= ₁CB.

Учитывая, что _{AC;\s\up10( –}CB;\s\up10( – , последнее равенство можно переписать так:

_{2AC;\s\up10( –} = _{1CB;\s\up10( –}.

Будем говорить, что точка C делит отрезок AB в отношении ₁:₂ , если выполнено_{2AC;\s\up10( –} = _{1CB;\s\up10( –}. Такое определение означает, что C может лежать на прямой AB за пределами отрезка AB, если ₁:₂ отрицательно. Число  = ₁/₂ (AC;\s\up10( – = CB;\s\up10( –) называется простым отношением точек A, B, C и обозначается (AB, C) или (ABC).

Пусть нам известны координаты концов отрезка: A(x₁, y₁, z₁), B(x₂, y₂, z₂). Требуется найти координаты точки C(x, y, z), которая делит этот отрезок в отношении ₁:₂. Из равенства _{2AC;\s\up10( –} = _{1CB;\s\up10( –} следует, что

^{x =} , ^{y =} , ^{z =} .

В частности, если C делит отрезок AB пополам, то

x = , y = , z = .

4.Ортогональная проекция вектора на направление. Осью будем называть прямую, на которой заданы начало отсчета, масштаб (единица длины) и положительное направление.

Ортогональной проекцией вектора на направление (ось)l называется число, равное длине отрезка A₁B₁, где A₁ и B₁  основания перпендикуляров, опущенных из концов вектора на направлениеl, взятое со знаком плюс, если направление вектора совпадает с направлениемl и со знаком минус, если направление вектора 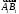противоположно направлениюl.

Проекцию вектора на направлениеl будем обозначать .

Свойства ортогональной проекции вектора на направление.

1.Проекция вектора на направление равна произведению его длины на косинус угла между вектором и положительным направлением оси: , где .

2. Проекция суммы векторов на направление l равна сумме проекций слагаемых на это направление: .

3. Проекция произведения вектора на число на направлениеl равна произведению этого числа на проекцию вектора на это направление:.

3. Скалярное произведение векторов

1.Скалярным произведением векторов иназывается действительное число, равное произведению длин векторов на косинус угла между ними.

Скалярное произведение векторов иобозначаетсяили. Итак,

.

2. Свойства скалярного произведения двух векторов.

1. (коммутативность);

2. 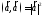(скалярный квадрат вектора равен квадрату его длины);

3. ;

4. (линейность);

5. (линейность);

6. ;

7.  0, и = 0  = (положительная определенность).

8. если , то;

9. если , то либо хотя бы один из векторовиравен нулю, либоиортогональны.

Так как направление нуль-вектора произвольно, то девятое свойство можно переформулировать как необходимое и достаточное условие ортогональности векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

Из определения скалярного произведения и свойств косинуса непосредственно вытекает неравенство Коши-Буняковского. Для любых векторов иимеем

.

При этом, если 0, то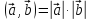тогда и только тогда, когда, где.

3. Механический смысл скалярного произведения заключается в следующем: если материальная точка под воздействием силы перемещается на вектор, то совершаемая этой силой работа равна скалярному произведениюна: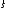

.

4. Из свойств скалярного произведения вытекает, что линейные комбинации векторов можно перемножать как многочлены. Возьмем в пространстве векторов базис . Тогда для векторови имеем

.

Здесь - метрические коэффициенты. Составим из метрических коэффициентов матрицу

Матрица Г называется матрицей Грама скалярного произведения для базиса е. Используя матрицу Грама, можно получить формулу для вычисления

.

Свойства матрицы Грама.

1⁰. Матрица Грама симметрична относительно главной диагонали.

2⁰.Диагональные элементы матрицы Грама строго положительны.

3⁰. Для матрицы Грама и любого n-мерного столбца х выполняется условие х ^ТГх  0.

Равенства

и =

Позволяют по координатам векторов и метрическим коэффициентам базиса находить длины векторов и углы между ними.

Базис е = (е₁,е₂, ... ,е_n) (на прямой, на плоскости или в пространстве называется ортонормированным, если

Длины векторов ортонормированного базиса равны единице:

Матрица Грама для ортонормированного базиса имеет вид

.

Ортонормированный базис в пространстве V² обычно обозначается , в пространствеV³  .

5. Пусть в ортонормированном базисе заданы векторы

, .

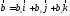В ортонормированном базисе скалярное произведение двух векторов равно сумме попарных произведений их соответствующих координат.

Вычисление длины вектора в ортонормированном базисе.

Вычисление угла между векторами в ортонормированном базисе

, откуда:

.

Вычисление координат орта вектора в ортонормированном базисе

Вычисление ортогональной проекции вектора на направление в ортонормированном базисе

.

Замечание. Если , то. Аналогично,. Таким образом, координаты вектора в ортонормированном базисе являются его ортогональными проекциями на направления, заданные соответствующими ортами.

Косинусы углов, которые отличный от нуля вектор образует с векторами ортонормированного базиса, называются направляющими косинусами.

.

Направляющие косинусы удовлетворяют соотношению

.

Из полученных выражений для направляющих косинусов видно, что они совпадают с координатами орта вектора.

.

Если A(x₁, y₁, z₁), B(x₂, y₂, z₂), то AB;\s\up10( – (x₂ – x₁, y₂ – y₁, z₂ – z₁) , то

AB;\s\up10( –= .

Обозначим (A, B) – расстояние между точками A и B. Тогда (A, B) вычисляется по той же формуле. Отметим, что эта функция обладает следующими свойствами:

1. (A, B) = (B, A);

2. (A, B) + (B, C)  (A, C) (неравенство треугольника);

3. (A, B)  0, и (A, B) = 0  A = B.

6. Если задан некоторый вектор , тоортогональной составляющей произвольного вектора вдоль вектора называется такой вектор , который коллинеарен, причем разностьперпендикулярна вектору.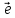

Аналогично, ортогональной составляющей вектора в плоскости называется вектор , компланарный плоскости, причем разностьперпендикулярна этой плоскости.