
- •Глава 1. Матрицы и определители
- •§1. Матрицы
- •1. Понятие матрицы
- •2. Квадратные матрицы
- •3. Действия с матрицами
- •Тогда суммарная производительность (за рабочий день) будет:
- •§2. Определители. Свойства. Вычисление
- •§3. Обратная матрица.
- •§4. Ранг матрицы
- •Идея практического метода вычисления ранга матрицы
- •Типовой пример. Найти ранг и указать какой-нибудь базисный минор матрицы .
- •Глава 2
- •§2. Решение линейных систем с помощью обратной матрицы. Правило Крамера. Теорема Кронекера-Капелли
- •§2. Метод Гаусса (метод последовательного исключения неизвестных) решения систем линейных уравнений
- •§4. Однородная система линейных алгебраических уравнений
- •Глава 3 линейные (векторные) пространства
- •§1. Понятие линейного пространства.
- •§ 2. Линейная зависимость и независимость систем векторов. Базис и размерность
- •Типовые примеры.
- •§ 3. Евклидовы пространства
- •Типовые примеры.
- •3.Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида
- •4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.
- •§4.Унитарное пространство
- •§5. Определение линейного оператора. Матрица линейного оператора.
- •§ 5. Собственные векторы и собственные значения матриц.
- •§6. Симметрические операторы. Квадратичные формы и их применения
- •Типовые примеры.
§2. Решение линейных систем с помощью обратной матрицы. Правило Крамера. Теорема Кронекера-Капелли
1.
Систему можно рассматривать как матричное
уравнение
![]() .
Пусть
матрица
.
Пусть
матрица![]() – невырожденная, тогда существует
обратная к ней матрица
– невырожденная, тогда существует
обратная к ней матрица![]() Умножим обе части данного равенства
слева на
Умножим обе части данного равенства
слева на![]() Получим
Получим
![]() Но
Но
![]() тогда
тогда![]() ,
а поскольку
,
а поскольку![]()
Итак, решением системы является произведение матрицы, обратной к А, на столбец свободных членов системы.
Типовые примеры.
1)
Решите систему
 .
.
►Матрица системы имеет вид
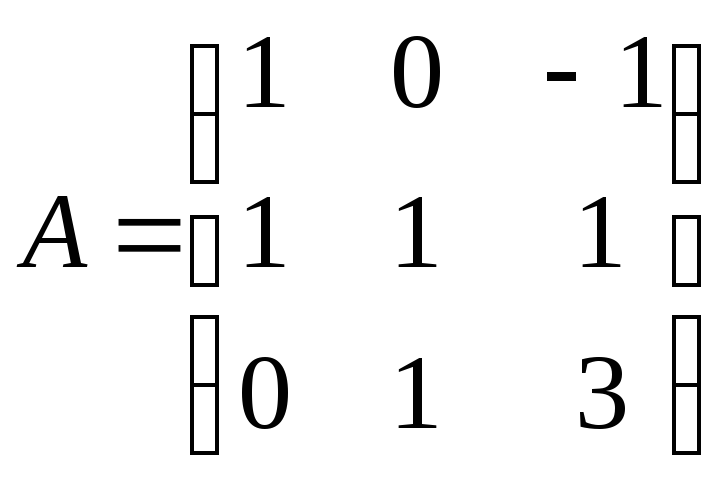
Она невырожденная, так как соответствующий ей определитель
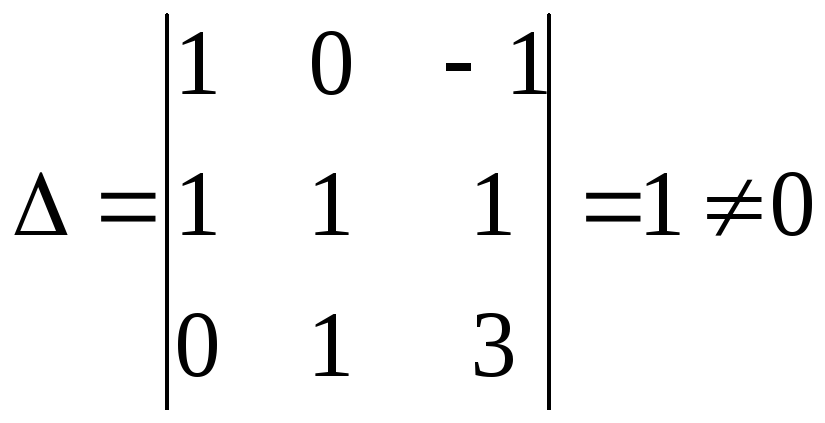 .
.
Следовательно,
решение системы может быть по формуле
![]() ,
где X
– матрица, состоящая из неизвестных, В
– матрица, состоящая из свободных
членов, А-1
– обратная матрица для матрицы А.
Обратную матрицу А-1
найдем по формуле
,
где X
– матрица, состоящая из неизвестных, В
– матрица, состоящая из свободных
членов, А-1
– обратная матрица для матрицы А.
Обратную матрицу А-1
найдем по формуле
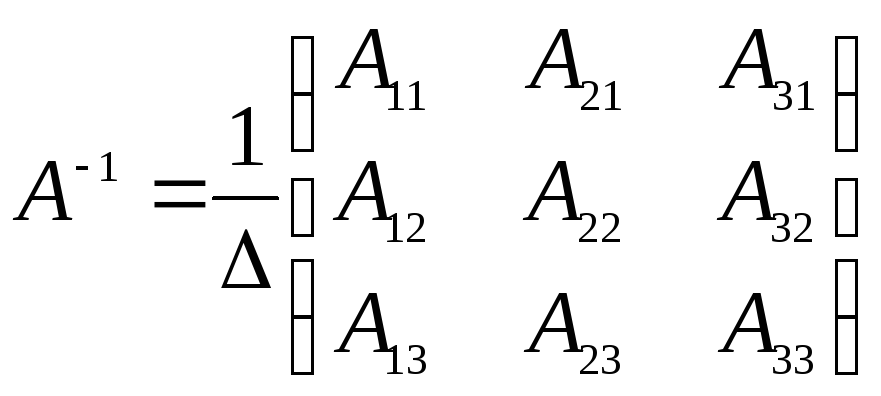
Определим алгебраические дополнения Аik элементов данной матрицы. Получим
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
Тогда
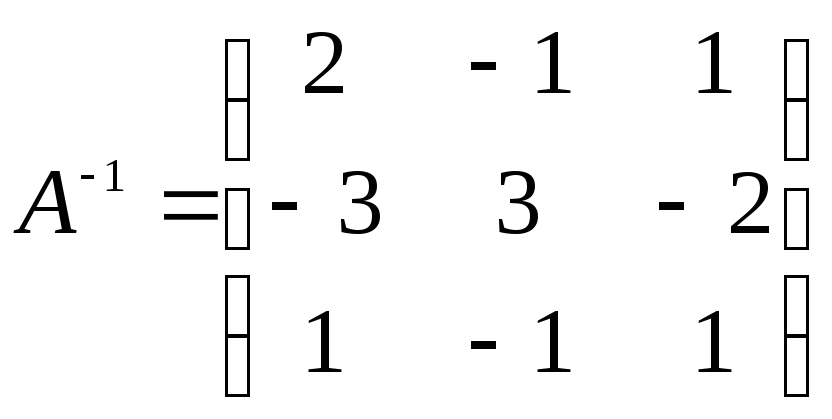
В данном случае матричное равенство X = A-1B может быть записано в виде
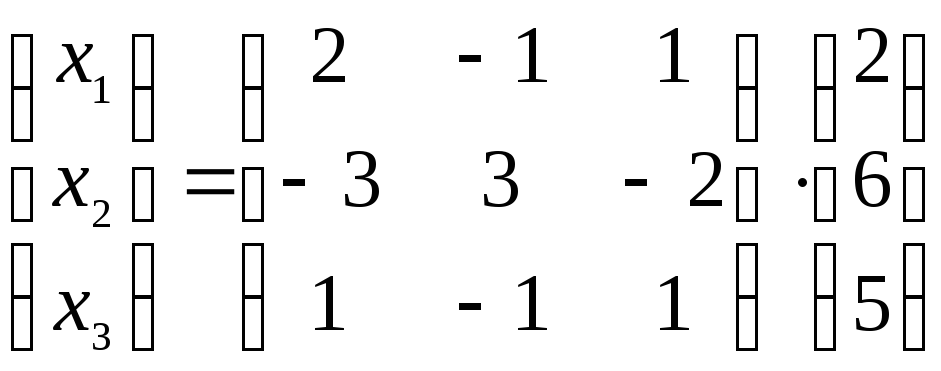
откуда
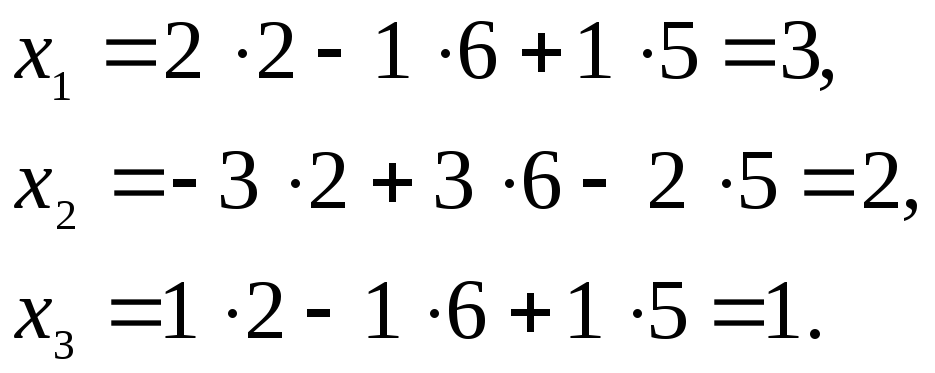 ◄
◄
2)
Решить систему
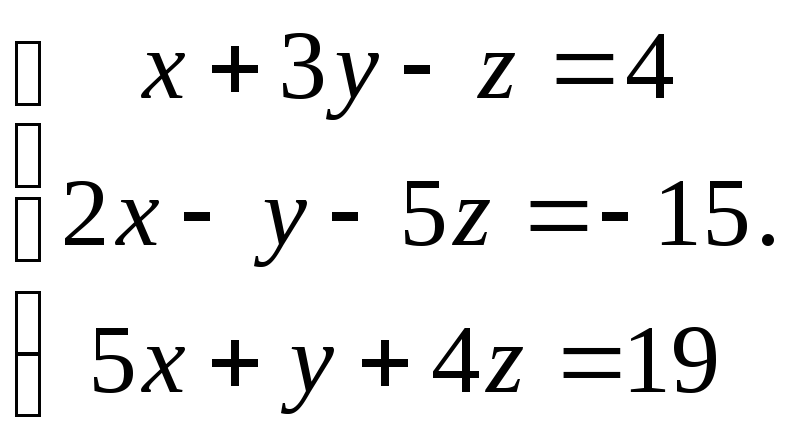
►Имеем
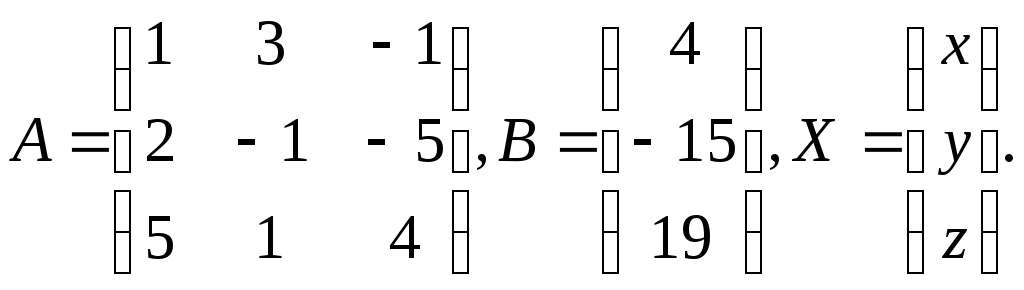
![]() Найдем
Найдем![]() :
:
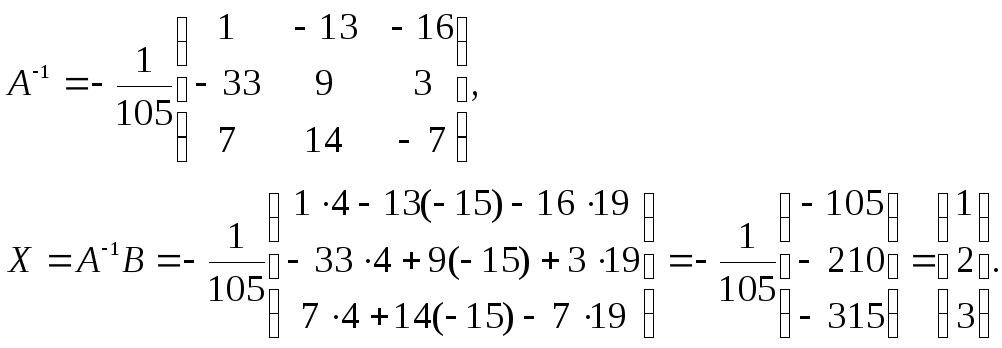
Таким
образом,
![]() .◄
.◄
2. Правило Крамера. Рассмотрим систему, у которых число уравнений равно числу неизвестных (такие системы называют квадратными).
Пусть
дана система
![]() линейных уравнений с
линейных уравнений с![]() неизвестными:
неизвестными:
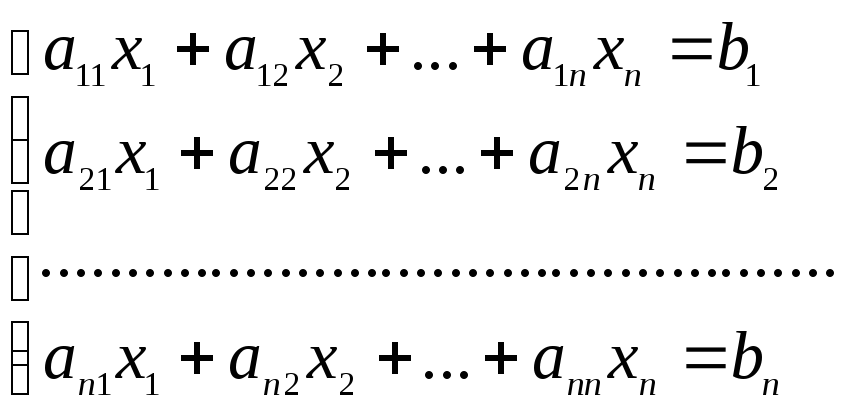
Определитель
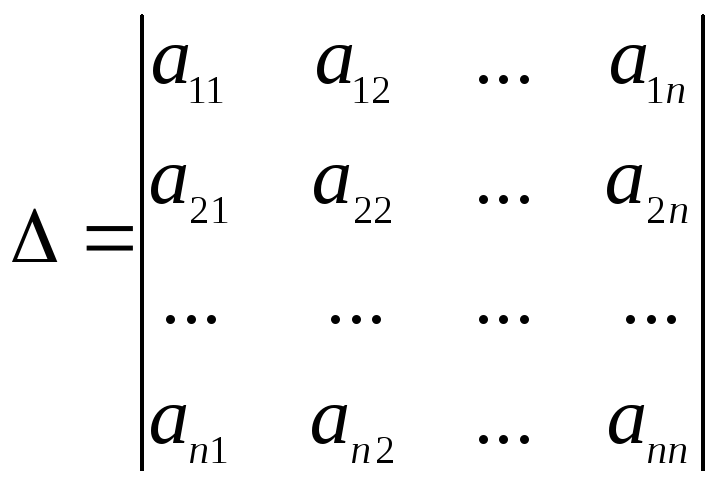 ,
,
составленный из коэффициентов при неизвестных, называется определителем системы.
ТЕОРЕМА.
Если
определитель
![]() квадратной системы отличен от нуля, то
эта система имеет единственное решение.
Это решение может быть найдено по
формулам
квадратной системы отличен от нуля, то
эта система имеет единственное решение.
Это решение может быть найдено по
формулам
![]() ,
,
где
![]() – определитель, получаемый из определителя
– определитель, получаемый из определителя![]() заменой
заменой![]() -го
столбца на столбец свободных членов.
-го
столбца на столбец свободных членов.
Формулы для неизвестных носят название формул Крамера.
Типовой пример. Решить с помощью формул Крамера систему уравнений
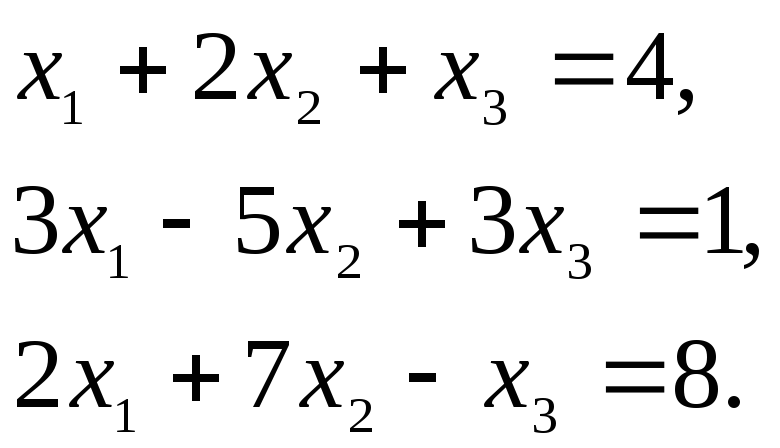
►Убедимся прежде всего в том, что определитель системы отличен от нуля:
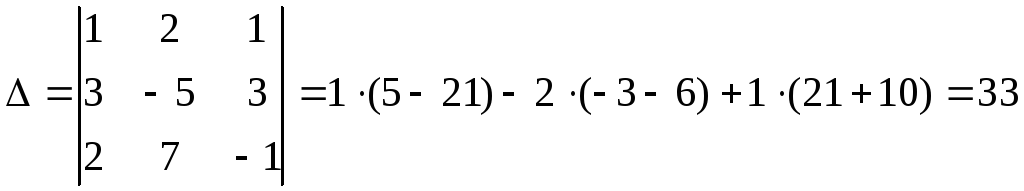 .
.
Вычислим теперь остальные, входящие в формулы Крамера, определители:
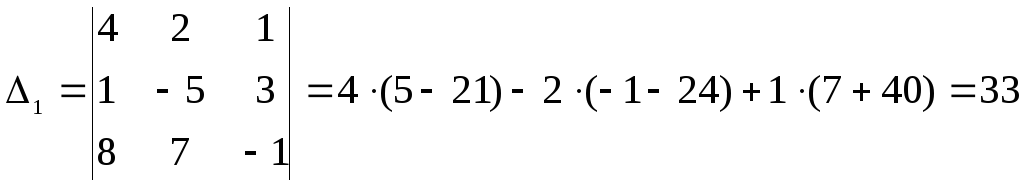 ,
,
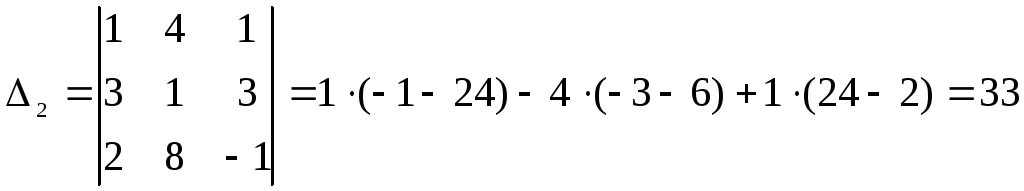 ,
,
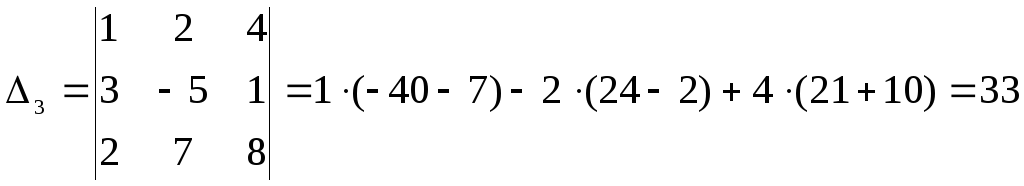 .
.
Подставив полученные значения определителей в формулы Крамера, имеем
![]()
Правильность
представленного решения можно проверить
подстановкой значений
![]() в исходную систему уравнений. ◄
в исходную систему уравнений. ◄
3.
Критерий совместности системы линейных
уравнений.
Рассмотрим снова произвольную систему
![]() линейных уравнений с
линейных уравнений с![]() неизвестными, которую запишем, как и
раньше, в матричной форме:
неизвестными, которую запишем, как и
раньше, в матричной форме:
![]() ,
,
где
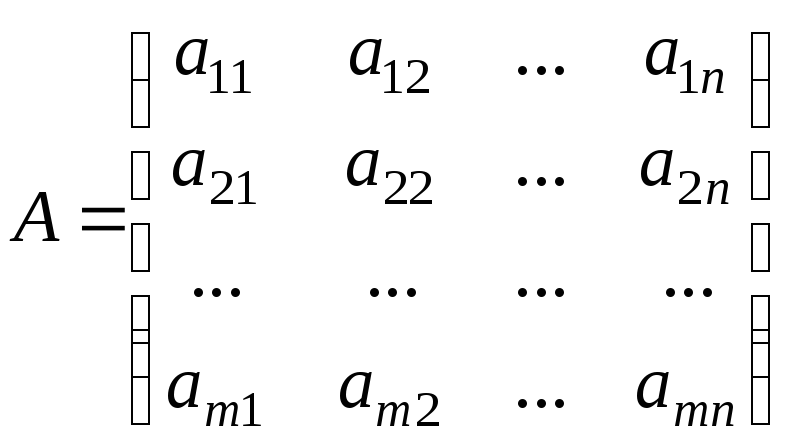 ,
,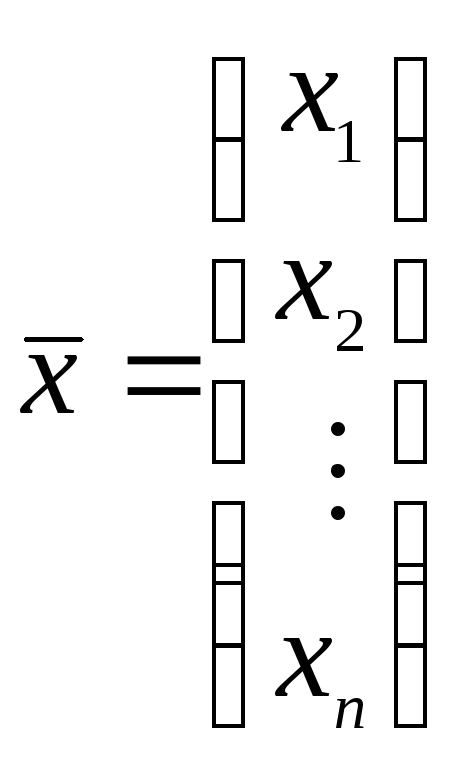 ,
,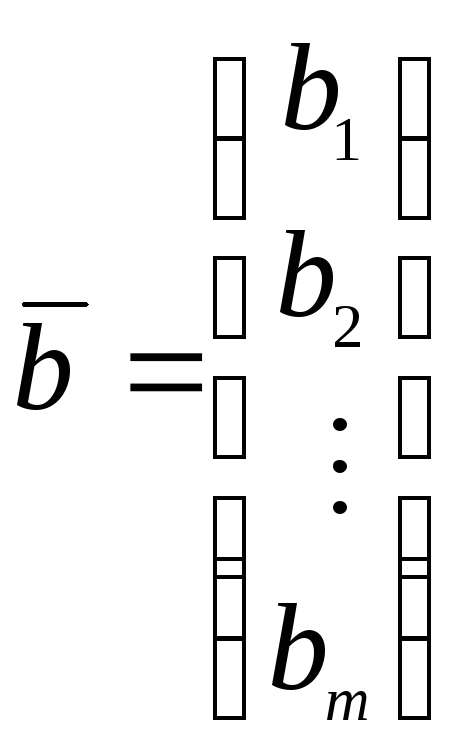 .
.
Матрицу
![]() называютматрицей
системы , а
матрицу, полученную из матрицы
называютматрицей
системы , а
матрицу, полученную из матрицы
![]() добавлением столбца свободных членов
добавлением столбца свободных членов![]() ,
–расширенной
матрицей системы.
Обозначим расширенную матрицу системы
символом
,
–расширенной
матрицей системы.
Обозначим расширенную матрицу системы
символом
![]() :
:
 .
.
Очевидно,
что ранги матриц
![]() и
и![]() связаны неравенством
связаны неравенством
![]() .
.
Ранг
матрицы
![]() может быть лишь на единицу больше ранга
матрицы
может быть лишь на единицу больше ранга
матрицы![]() .
.
Вопрос о совместности системы полностью решается следующей теоремой.
ТЕОРЕМА
(Кронекера-Капелли).
Для того
чтобы система линейных уравнений была
совместна, необходимо и достаточно,
чтобы ранг матрицы этой системы был
равен рангу ее расширенной матрицы,
т.е. чтобы
![]() .
.
Если
ранг матрицы системы равен рангу
расширенной матрицы, т.е.
![]() ,
то ранг матрицы системы называют
рангом
системы.
,
то ранг матрицы системы называют
рангом
системы.
