§3. Обратная матрица.

1. Как известно, для каждого числа существует такое число, что. Числоназывается обратным для. Если мы зафиксируем натуральное числои будем рассматривать квадратные матрицы-го порядка, то в этом множестве матриц единичная матрицабудет играть роль единицы. Естественно поставить вопрос о существовании обратной матрицы, т.е. такой матрицы, которая в произведении с данной матрицей дает единичную.

Пусть – квадратная матрица-го порядка. Квадратная матрица(того же порядка) называется обратной для, если

.

Матрицу, обратную к матрице , принято обозначать символом.

2. Способы вычисления обратной матрицы. Если для квадратной матрицы существует обратная матрица, то справедливо равенство, где– единичная матрица. Переходя в этом равенстве к определителям (и учитывая свойство 9 определителей), имеем, или. Отсюда заключаем, что(в противном случае левая часть последнего равенства равнялась бы нулю). Этим доказано, что если, то для матрицыне существует обратной. Другими словами, условиеявляется необходимым условием существования обратной матрицы. Оказывается, это условие является и достаточным.

Лемма. Если обратная матрица существует, то она единственна.

Квадратная матрица называетсяневырожденной, если ее определитель не равен нулю ( ). В противном случае матрицаназываетсявырожденной ( ).

Пусть матрица имеет вид

.

ТЕОРЕМА. Если – невырожденная матрица, то для нее существует обратная матрица, которая вычисляется по формуле

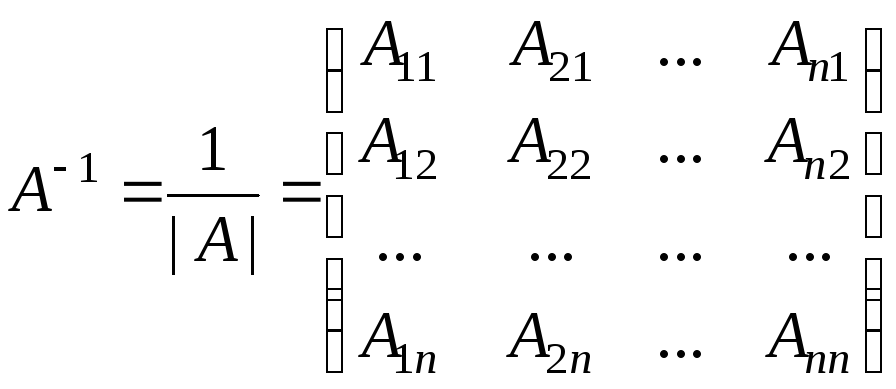, (5)

где – алгебраическое дополнение для элементаматрицы.

Замечание. Обратим внимание на расположение чисел в правой части формулы (5): число расположено не в -й строке и-м столбце, а наоборот, в-й строке и-м столбце. Таким образом, матрица, стоящая в правой части (5), является транспонированной матрицей алгебраических дополнений элементов матрицы.

Типовой пример. Найдите , если.

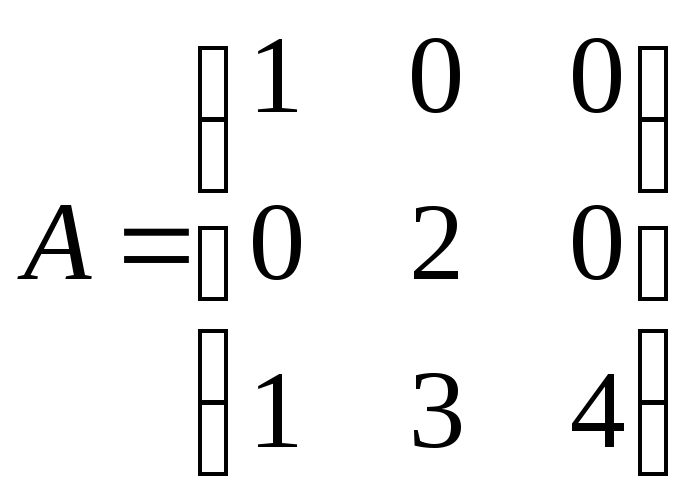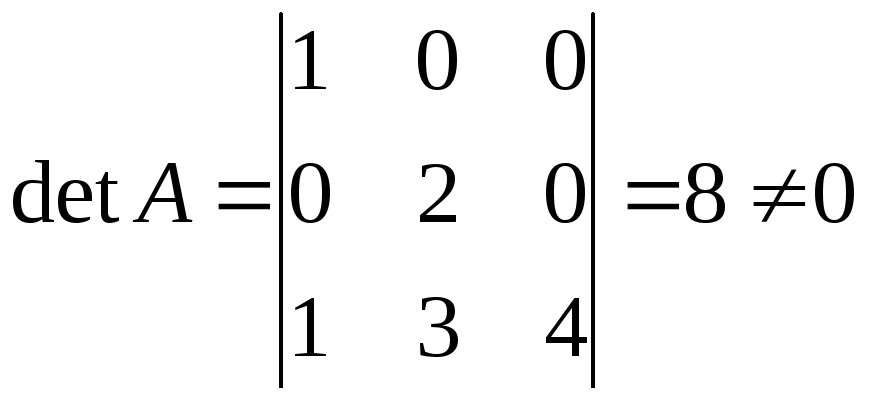► . – невырожденная матрица, следовательно, обратная для нее существует. Найдем ее по формуле:

.

Обратите внимание на индексацию алгебраических дополнений. Вычисляем алгебраические дополнения

; ; ;

; ; ;

; ; .

Тогда

.

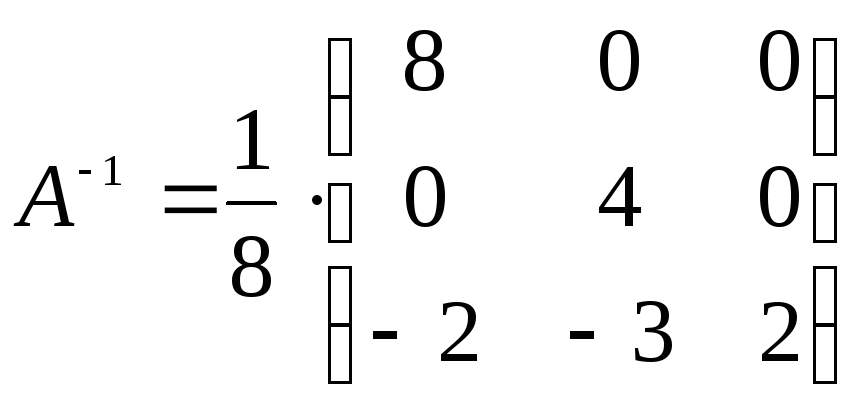Можно сделать проверку:

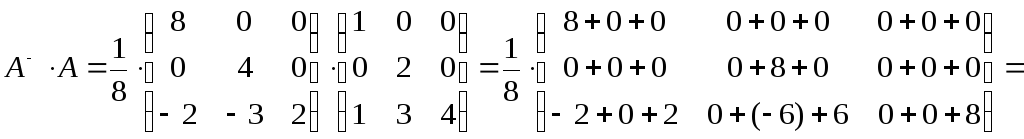
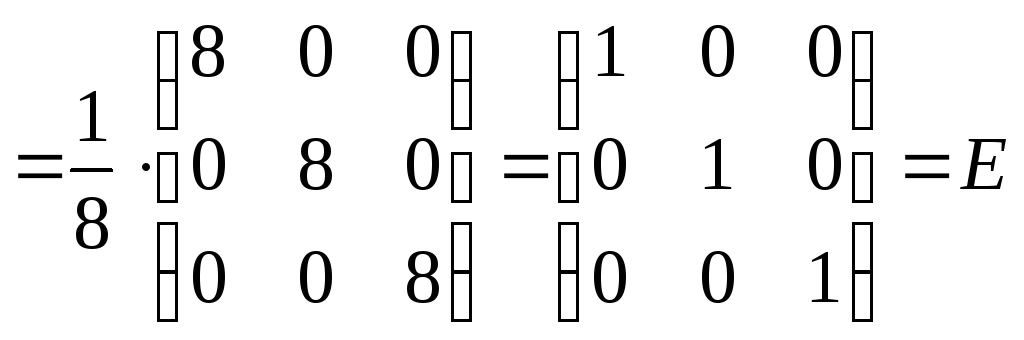. Значит, обратная матрица найдена верно.◄

3. Вычисление обратной матрицы методом элементарных преобразований. Элементарные преобразования матрицы.

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число .

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на любое число.

Чтобы найти матрицу, обратную данной, делаем следующее:

- для матрицы записываем прямоугольную матрицу, приписывая справа единичную матрицу;

- с помощью элементарных преобразований приводим матрицу к виду. Тогда. Эквивалентные матрицы обозначаются.

Типовой пример. Найти матрицу, обратную данной: .

►~(первую строку матрицы умножили на ) ~~~~

. Следовательно, .

Проверка: . ◄

С помощью обратной матрицы можно решать простейшие матричные уравнения, где неизвестной является матрица X. Это уравнения следующего вида

.

В этих уравнениях – матрицы таких размеров, что все операции умножения возможны и с обеих сторон от знаков равенств находятся матрицы одинаковых размеров. Если в первых двух уравнениях матрицаневырожденная, то их единственное решение записывается следующим образом соответственнои. Если в третьем матричном уравнении матрицы и невырождены, то его решение записывается в виде . Пример. В таблице приведены данные о дневной производительности пяти предприятий, выпускающих четыре вида продукции с потреблением трех видов ресурсов, а также количество рабочих дней в году каждого предприятия и цены каждого вида сырья:

Вид продукции	Производительность предприятий (изд. в день)					Затраты ресурсов ед веса/изд.
	1	2	3	4	5		1	2	3
1	4	5	3	6	7		2	3	4
2	0	2	4	3	0		3	5	6
3	8	15	0	4	6	4		4	5
4	3	10	7	5	4	5		8	6
	Кол-во раб. дней в году					Цены ед.сырья
	200	150	170	120	140	40		50	60

Требуется найти:

1) годовую производительность каждого предприятия по каждому виду продукции;

2) годовую потребность каждого предприятия по каждому виду ресурса;

3) годовую сумму кредитования каждого предприятия для закупки ресурсов, необходимых для выпуска продукции указанных видов и при определенном количестве рабочих дней.

►Введем следующие обозначения.

Данная матрица является матрицей производительности пяти предприятий по всем 4 видам продукции. Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду изделий. Следовательно, годовая производительность -го предприятия по каждому виду изделий получается умножением-го столбца матрицы А на количество рабочих дней в году для этого предприятия (к = 1,2,3,4,5)

А₁₁=0,79 А₂₁=0,16 А₃₁=0,02

А₁₂=0,16 А₂₂=0,8 А₃₂=0,1

А₁₃=0,02 А₂₃=0,1 А₃₃=0,96,

тогда .

Это матрица коэффициентов полных материальных затрат.

б) , т.е. валовый выпуск продукции 1-го, 2-го и 3-го цехов будут соответственно.

в) Найдем производственную программу каждого цеха (промежуточный продукт) по формуле (;)

;

;

;

;

;

;

;

;

.

В результате получим следующую таблицу:

Цех	Внутрипроизводственные потребления			Итого	Конечный продукт	Валовый выпуск
	1	2	3
1 2 3	0 48 0	37 0 19	0 40 80	37 88 99	200 100 300	237 186 400

г) Коэффициенты косвенных затрат определяются как разности полных внутрипроизводственных затрат и прямых затрат. В матричной форме:

; .◄

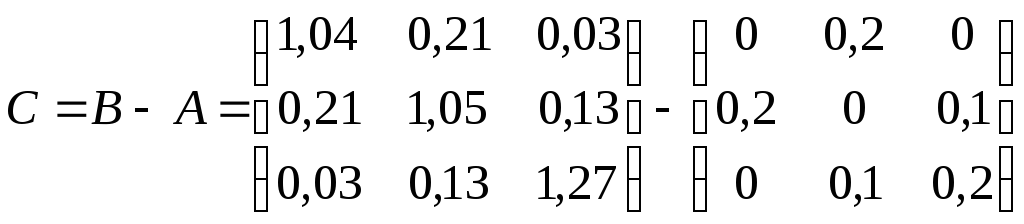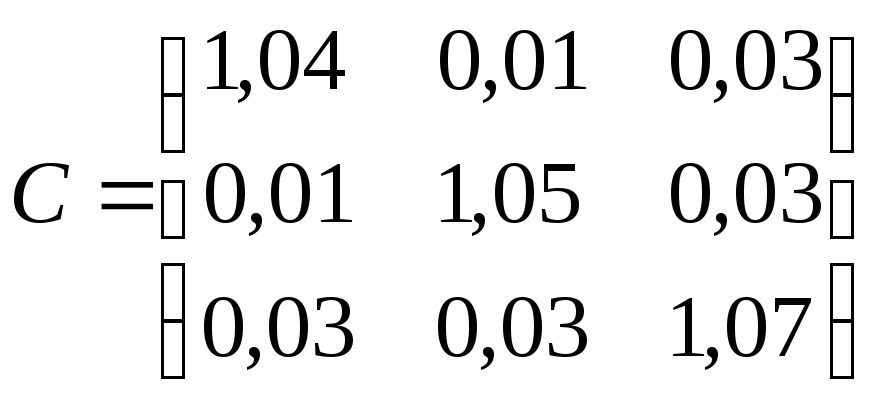4. Невырожденная квадратная матрица , для которой, называетсяортогональной. Свойства ортогональных матриц, играющих важную роль во многих приложениях, можно сформулировать в виде следующих теорем.

ТЕОРЕМА. Для ортогональной матрицы справедливо равенство.

ТЕОРЕМА. Каждая ортогональная матрица второго порядка , для которойможет быть представлена в виде, где - некоторое число, а каждая ортогональная матрица с - в виде.