Типовые примеры.
1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
.
►Следуя
алгоритму метода Лагранжа, выделим
вначале в квадратичной форме все члены,
содержащие
,
и дополним их до полного квадрата:
.
Сделаем
в этом выражении замену
и подставим его в квадратичную форму.
Получим:
.
Далее
выделим в
члены, содержащие
и проделаем с ними аналогичную процедуру:
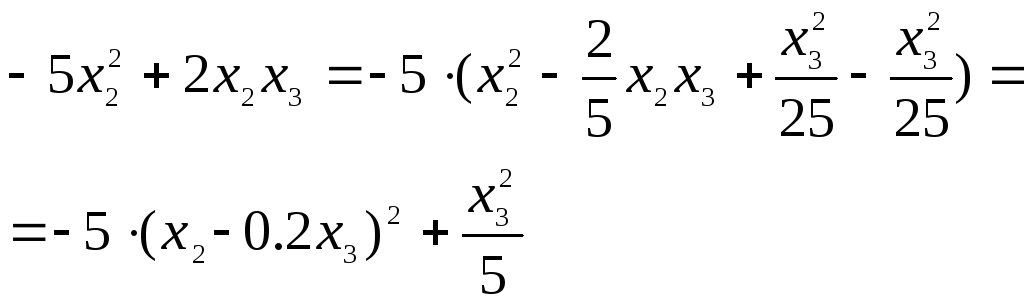
Если
положить
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также
,
тогда
канонический вид квадратичной формы есть
.
Соответствующее
преобразование от переменных
к переменным
имеет вид:
.◄
2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
.
►В
исходном базисе
матрица оператора, соответствующая
данной квадратичной форме, есть
.
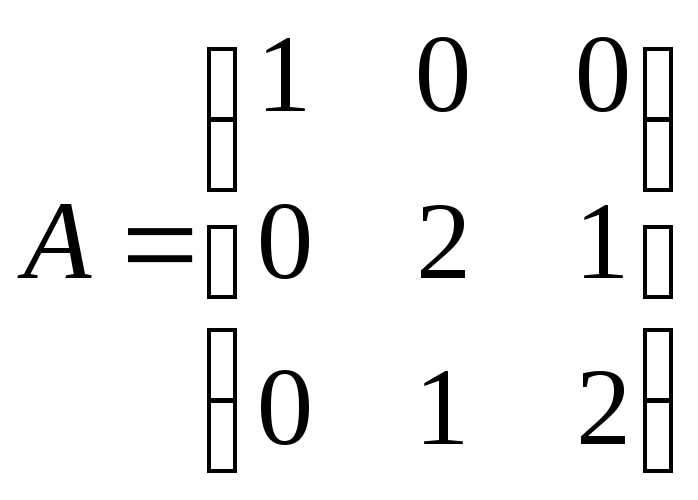Эта
матрица будет определять квадратичную
форму канонического вида в ортонормированном
базисе
,
составленном из собственных векторов
матрицы
.
Найдем их. Характеристическое уравнение
для матрицы
имеет вид
.
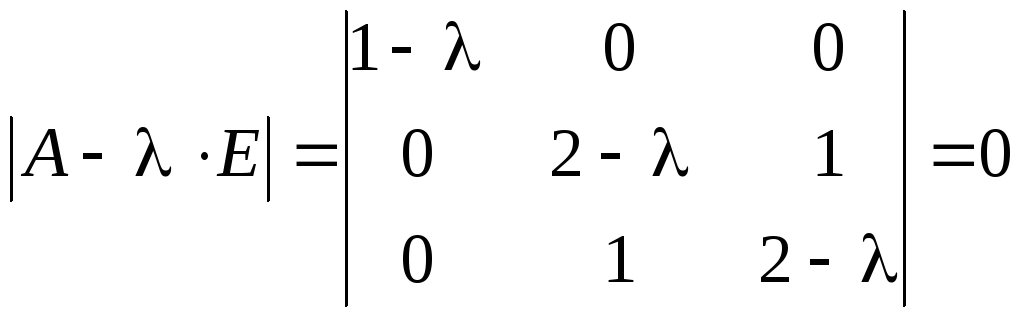Откуда следует
и
.
Как известно собственные векторы матрицы находятся из уравнений
.
Для
случая
имеем:
.
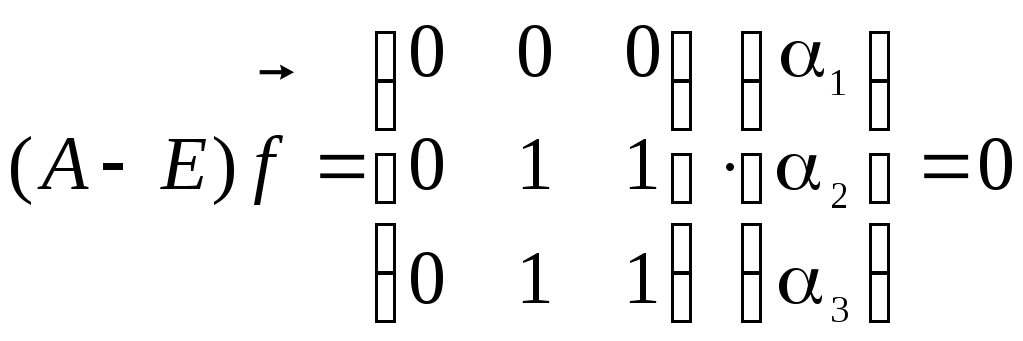Ранг
матрицы этой системы уравнений
(относительно
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина
принимает произвольные значения, а
величины
связаны соотношением
.
В качестве собственных можно выбрать,
например, векторы
Эти
векторы ортогональны:
(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор
к тому же и нормирован. Откуда следует
-
.
Нормируем теперь вектор
:
.
Для
случая
уравнение, определяющее собственный
вектор есть
.
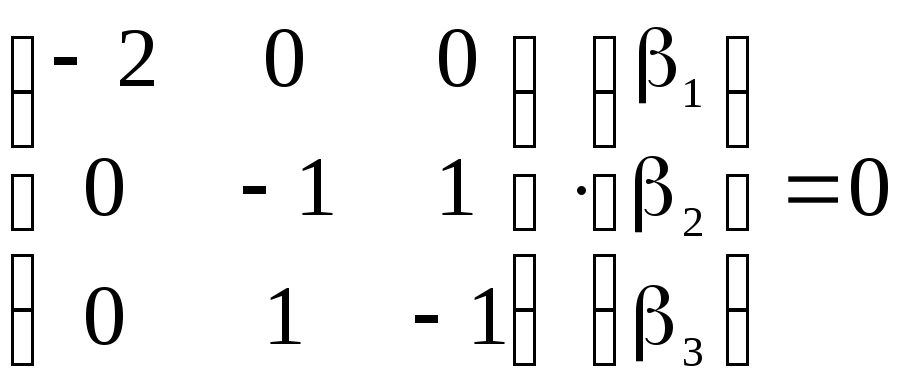Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например,
Отнормируем этот вектор:
.
Теперь можно составить искомую матрицу ортогонального преобразования:
.
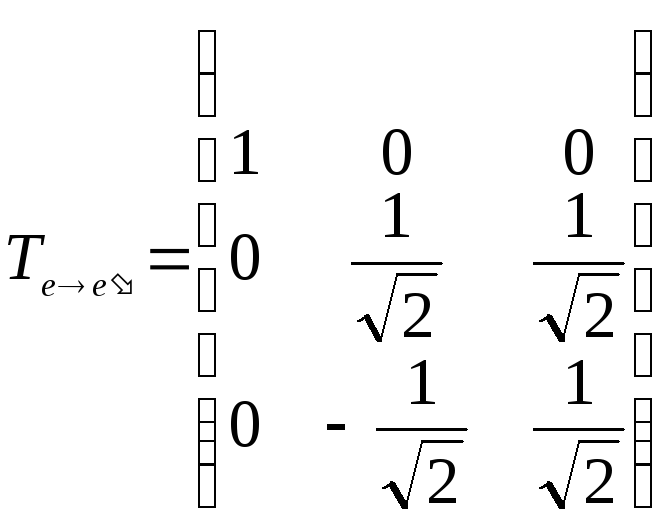Исходная квадратичная форма будет иметь следующий канонический вид
.
При
этом переменные
связаны с переменными
соотношением
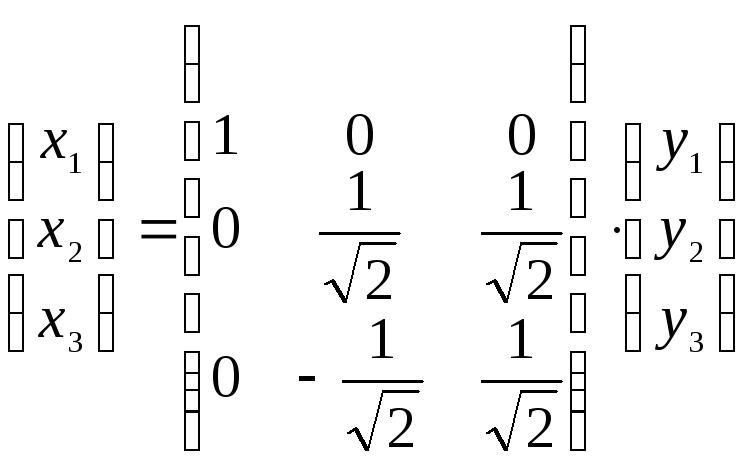или
.◄
3. Привести к главным осям квадратичную форму третьего порядка.
.
►Построим матрицу этой квадратичной формы:
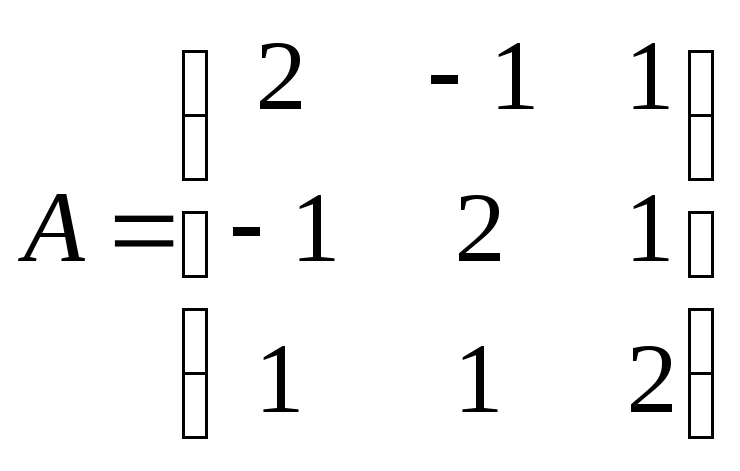
Найдём
собственные числа и векторы:
.
Простому корню 0 соответствует собственный
вектор
,
кратному корню 3 соответствуют два
собственных вектора:
,
.
Запишем матрицу перехода, предварительно
поделив каждый вектор на его модуль.
,
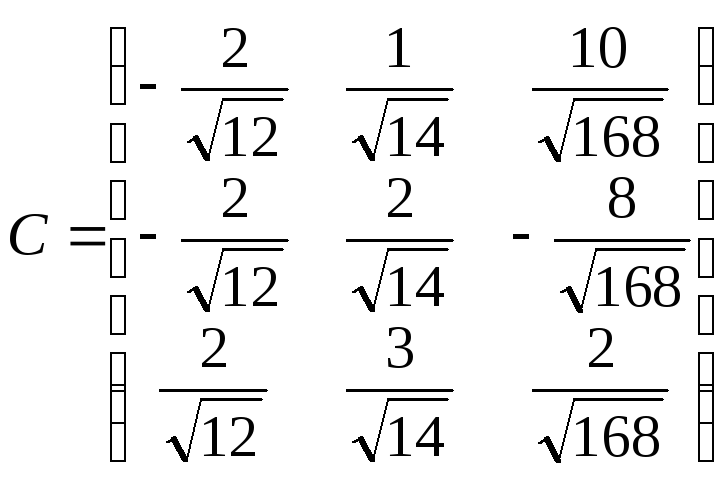а
квадратичная форма имеет вид:
.◄
4. (с дробными коэффициентами квадратичной формы). Привести к главным осям квадратичную форму третьего порядка.
.
►Сначала построим матрицу квадратичной формы.
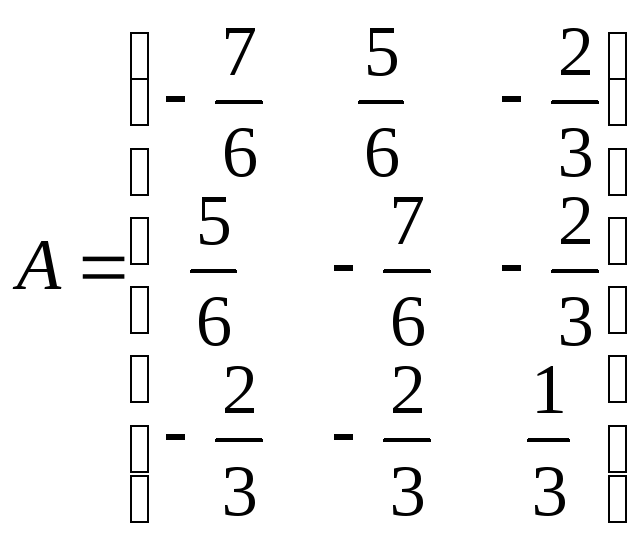
Найдём 3 собственных числа. λ = 1 , -1 , -2. Затем для каждого собственного числа найдём собственный вектор и нормируем его.
λ
=1 x=
λ
=-1 x=
.
λ
=-2 x=
Квадратичная
форма в новом базисе:
=
.◄
5. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
.
►Выделим
в этом выражении квадратичную форму
.
Это три первых слагаемых уравнения
.
Матрица
квадратичной формы равна
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
.
Его
корни таковы:
.
Найдём теперь собственные векторы,
соответствующие этим корням и ортонормируем
их. Для вектора
,
соответствующего
,
имеем
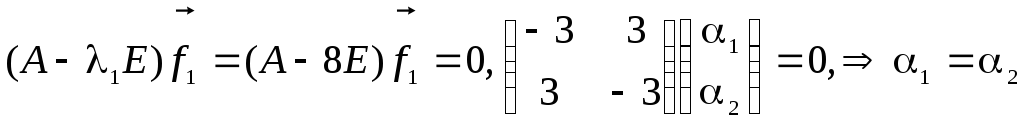
В
итоге собственный вектор, соответствующий
,
можно выбрать в виде
.
Аналогичная
процедура для собственного вектора
даёт:
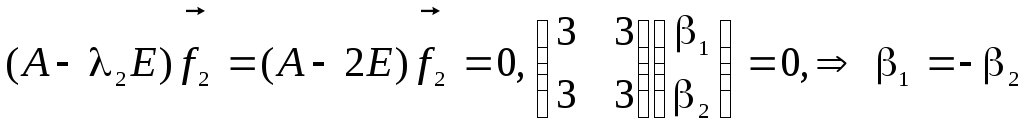
Откуда:
.
После нормировки полученных векторов имеем:
.
Эти
векторы представляют собой ортонормированный
базис новой системы координат. Матрица
ортогонального оператора, приводящего
квадратичную форму
к каноническому виду
,
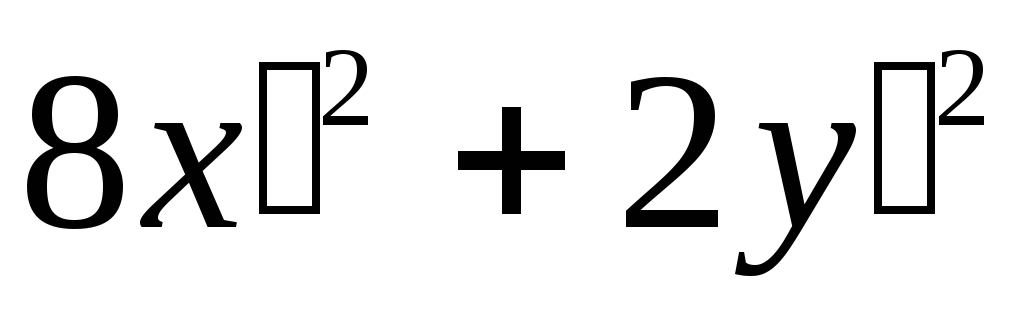есть
Связь
старых
и новых
координат определяется соотношением
.
Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду
.
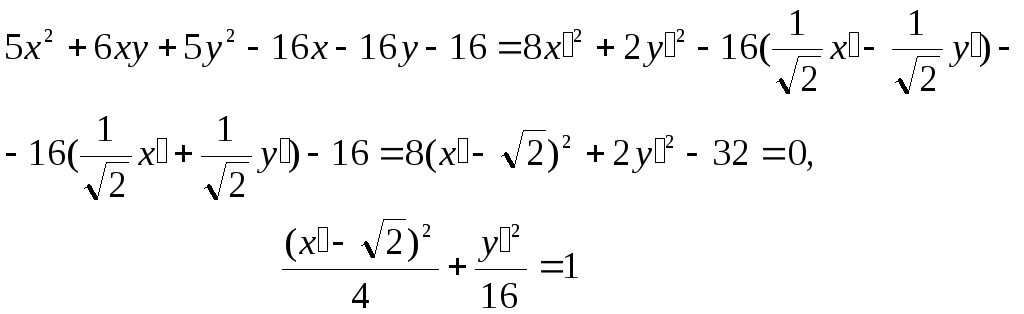Это есть каноническое уравнение эллипса
в системе координат
,которая
получается из исходной её поворотом на
угол
и
переносом начала координат в точку
.◄