§6. Симметрические операторы. Квадратичные формы и их применения

1. Симметрические операторы и их свойства. Линейный оператор называется симметрическим, если для любых вектороввыполняется.

Перечислим основные свойства симметрического линейного оператора:

1.Линейный оператор является симметрическим тогда и только тогда, когда его матрица в любом базисе симметрична.

2.Собственные векторы симметрического линейного оператора, соответствующие различным собственным значениям, ортогональны.

3.Всякому собственному числу кратности k симметрического оператора соответствует линейно независимая система из k собственных векторов.

4.Для всякого симметрического линейного оператора существует базис в пространстве , состоящий из его собственных векторов.

2. Билинейные и квадратичные формы. Билинейной формой на пространстве называется отображение, сопоставляющее каждой паре векторов число, причём:

.

Всякую билинейную форму можно задать с помощью матрицы билинейной формы:

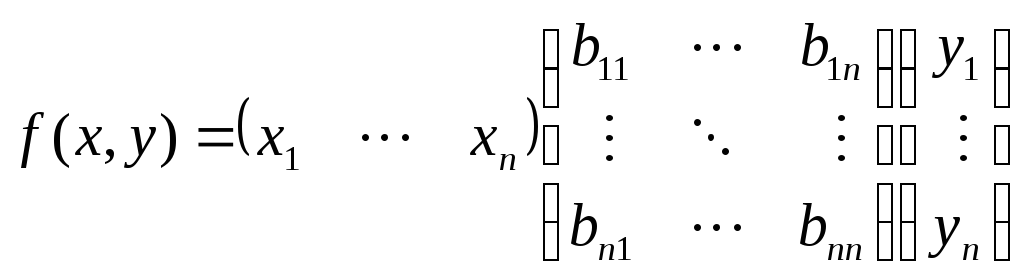
То есть, .

Замечание. Обычное скалярное произведение также является билинейной формой и соответствует единичной матрице .

Если положить для билинейной формы, то полученное отображениеназываетсяквадратичной формой на пространстве . Таким образом,квадратичной формой переменных, принимающих числовые значения, называется числовая функция вида

,

где - числа, называемые коэффициентами квадратичной формы.

Матрицей квадратичной формы переменных, называется симметрическая матрица порядка, элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный вой строкеом столбце, равен половине коэффициента при в квадратичной форме.

Рангом квадратичной формы называется ранг её матрицы. Квадратичная форма может быть записана в матричном виде где матрица квадратичной формы и .

Квадратичная форма называется канонической (имеет канонический вид), если коэффициенты при , то есть, если матрица квадратичной формы диагональная и следовательно

.,

где не все коэффициенты равны нулю.

ТЕОРЕМА (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны .

Алгоритм приведения квадратичной формы к главным осям:

1.Построить матрицу квадратичной формы.

2.Найти собственные числа и векторы, записать квадратичную форму (коэффициентами при квадратах новых переменных будут найденные собственные числа).

3.Нормировать собственные векторы и записать матрицу перехода от старого базиса к новому (а именно, состоящему из найденных векторов).

Квадратичная форма называется положительно (отрицательно) определённой, если при всех и положительно (отрицательно) полуопределённой, если при всех .

ТЕОРЕМА (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны, то есть, чтобы

Здесь -угловые миноры матрицы квадратичной формы.

Следствие. Для того чтобы квадратичная форма была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом: