
- •Глава 1. Матрицы и определители
- •§1. Матрицы
- •1. Понятие матрицы
- •2. Квадратные матрицы
- •3. Действия с матрицами
- •Тогда суммарная производительность (за рабочий день) будет:
- •§2. Определители. Свойства. Вычисление
- •§3. Обратная матрица.
- •§4. Ранг матрицы
- •Идея практического метода вычисления ранга матрицы
- •Типовой пример. Найти ранг и указать какой-нибудь базисный минор матрицы .
- •Глава 2
- •§2. Решение линейных систем с помощью обратной матрицы. Правило Крамера. Теорема Кронекера-Капелли
- •§2. Метод Гаусса (метод последовательного исключения неизвестных) решения систем линейных уравнений
- •§4. Однородная система линейных алгебраических уравнений
- •Глава 3 линейные (векторные) пространства
- •§1. Понятие линейного пространства.
- •§ 2. Линейная зависимость и независимость систем векторов. Базис и размерность
- •Типовые примеры.
- •§ 3. Евклидовы пространства
- •Типовые примеры.
- •3.Матрица Грамма.Матрицей Грамадля системы векторовназывается симметричная матрица вида
- •4. Ортогональное разложение векторов. Говорят, что векторортогонален к подпространству, если векторортогонален любому вектору из этого подпространства.
- •§4.Унитарное пространство
- •§5. Определение линейного оператора. Матрица линейного оператора.
- •§ 5. Собственные векторы и собственные значения матриц.
- •§6. Симметрические операторы. Квадратичные формы и их применения
- •Типовые примеры.
Глава 1. Матрицы и определители
§1. Матрицы
1. Понятие матрицы
Прямоугольная
таблица чисел, содержащая
![]() строк и
строк и![]() столбцов, называетсяматрицей размеров
столбцов, называетсяматрицей размеров
![]() .
Для записи матрицы используются круглые
или квадратные или двойные вертикальные
скобки:
.
Для записи матрицы используются круглые
или квадратные или двойные вертикальные
скобки:
Числа,
входящие в описание матрицы, называемые
ее элементами
(или
компонентами),
характеризуются как своим значением,
так и номерами строк и столбцов. Условимся
обозначать элемент матрицы, расположенный
в i-й
строке и j-м
столбце, как
![]() ).Часто вместо
подробной записи употребляют сокращенную:
).Часто вместо
подробной записи употребляют сокращенную:
![]() или даже
или даже![]() .
С помощью матриц удобно записывать
некоторые экономические зависимости.
.
С помощью матриц удобно записывать
некоторые экономические зависимости.
Пример
Имеется предприятие, выпускающее 4 вида изделий из 3-х видов сырья. Табл. 1 представляет расход каждого вида сырья на выпуск 1 единицы продукции и их запас на предприятии.
Таблица 1
|
Виды Виды прод сырья. |
Затраты сырья на 1 ед.про- дукции (усл. ед) |
Запасы ресурсов | |
|
1 2 3 4 | |||
|
I |
|
3 5 1 4 |
200 |
|
II |
2 10 7 8 |
300 | |
|
III |
6 1 5 9 |
220 | |
Она может быть записана в виде матрицы распределения ресурсов на выпуск 1ед. каждого вида продукции:
![]() =
=
Размерность
этой матрицы 34.
В этой записи матричный элемент
![]() =7
показывает, сколько ресурса второго
вида необходимо затратить для производства
1 ед. третьего вида продукции. Запас
ресурсов можно записать в виде такой
матрицы:
=7
показывает, сколько ресурса второго
вида необходимо затратить для производства
1 ед. третьего вида продукции. Запас
ресурсов можно записать в виде такой
матрицы:
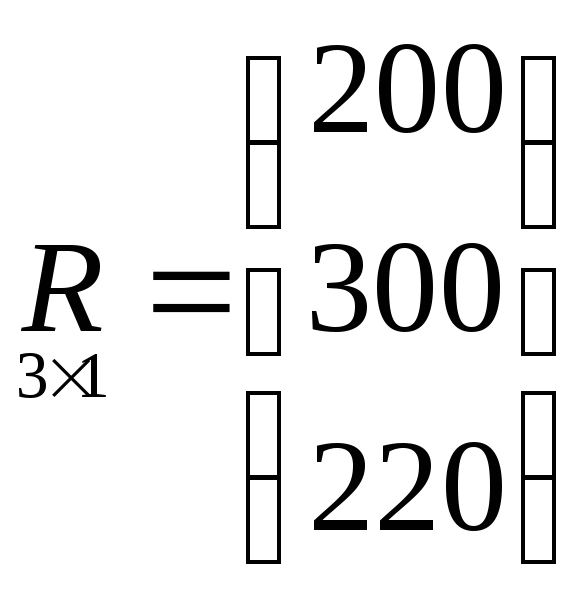
Матрица
состоит из 3-х строк и одного столбца.
Элемент
![]() показывает запас ресурса второго вида.
показывает запас ресурса второго вида.
Матрица, все элементы которой равны нулю, называется нулевой. Назовём матрицу произвольных размеров трапециевидной, если она имеет вид:

где
![]() отличны от нуля.
отличны от нуля.
2. Квадратные матрицы
Если
число строк матрицы равно числу ее
столбцов, то матрица называется
квадратной,
а число
![]() ее строк (равное числу столбцов) –порядком
квадратной матрицы:
ее строк (равное числу столбцов) –порядком
квадратной матрицы:
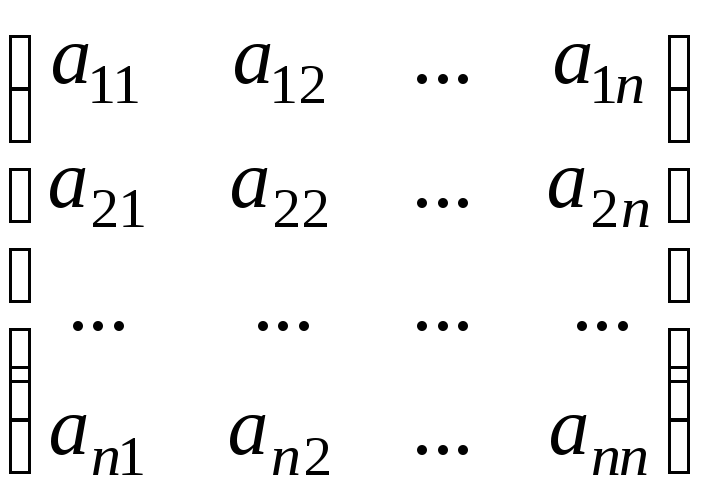 .
.
Элементы
![]() образуютглавную
диагональ
квадратной матрицы, а элементы
образуютглавную
диагональ
квадратной матрицы, а элементы
![]() –побочную
диагональ матрицы.
–побочную
диагональ матрицы.
Квадратная матрица называется треугольной, если все ее элементы, которые находятся ниже (или выше) главной диагонали, равны нулю, т.е. треугольная матрица имеет вид
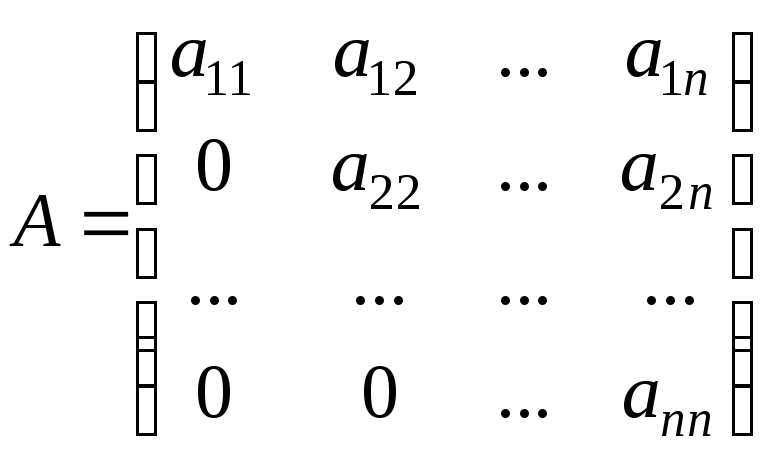 или
или
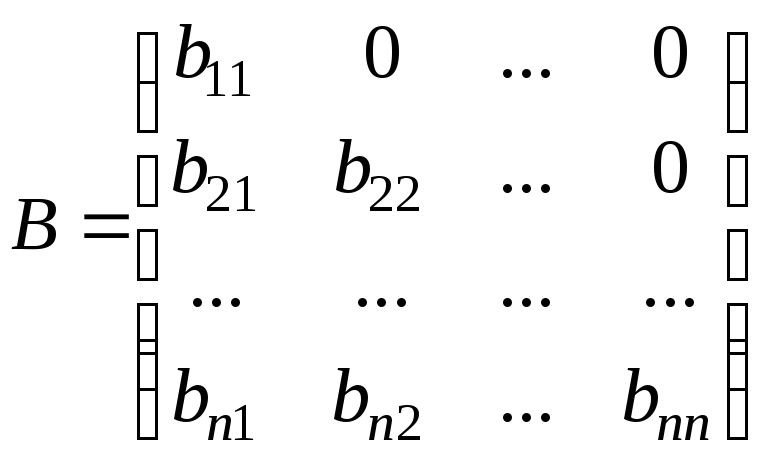 .
.
При
этом матрицу
![]() называютверхнетреугольной,
а матрицу
называютверхнетреугольной,
а матрицу
![]() –нижнетреугольной.
Матрица, у
которой элементы, расположенные вне
главной диагонали, равны нулю, называется
диагональной.
Если в диагональной матрице элементы
главной диагонали равны единице
(остальные нули), то матрица называется
единичной.
–нижнетреугольной.
Матрица, у
которой элементы, расположенные вне
главной диагонали, равны нулю, называется
диагональной.
Если в диагональной матрице элементы
главной диагонали равны единице
(остальные нули), то матрица называется
единичной.
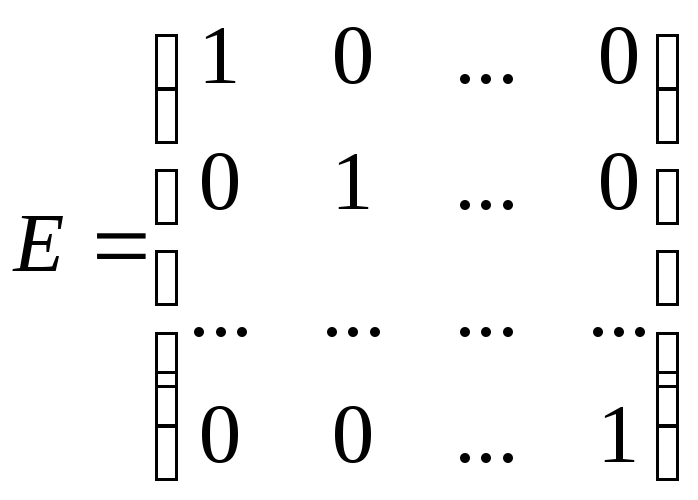 –единичная
матрица.
–единичная
матрица.
3. Действия с матрицами
Две
матрицы
![]() и
и![]() считаютсяравными,
если совпадают их размеры и
считаютсяравными,
если совпадают их размеры и
![]() при любых
при любых![]() и
и![]() .Сложение
матриц.
Складывать можно только матрицы с
одинаковым числом строк и столбцов,
т.е. матрицы одинаковых размеров. Суммой
матриц
.Сложение
матриц.
Складывать можно только матрицы с
одинаковым числом строк и столбцов,
т.е. матрицы одинаковых размеров. Суммой
матриц
![]() и
и![]() называется матрица
называется матрица![]() ,
элементы которой равны суммам
соответствующих элементов матриц
,
элементы которой равны суммам
соответствующих элементов матриц![]() и
и![]() ,
т.е.
,
т.е.![]() для любых индексов
для любых индексов![]() ,
,![]() .
.
Свойства сложения:
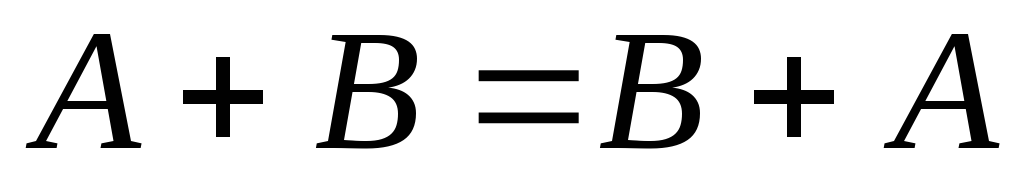 .
.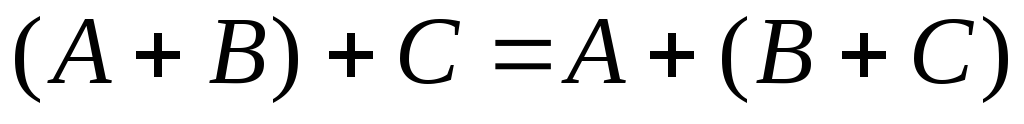 .
.
Если
 – нулевая матрица, то
– нулевая матрица, то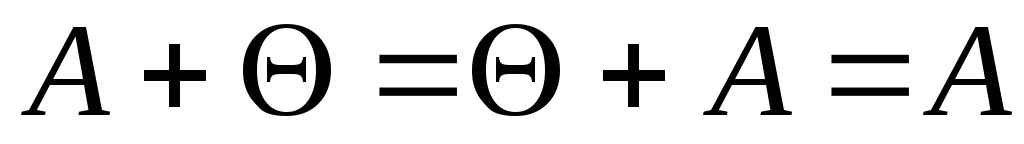 .
.
Умножение
матрицы на число.
Для того чтобы умножить матрицу
![]() на число
на число![]() ,
нужно каждый элемент матрицы
,
нужно каждый элемент матрицы![]() умножить на это число:
умножить на это число:![]() .
.
Свойства умножения матрицы на число:
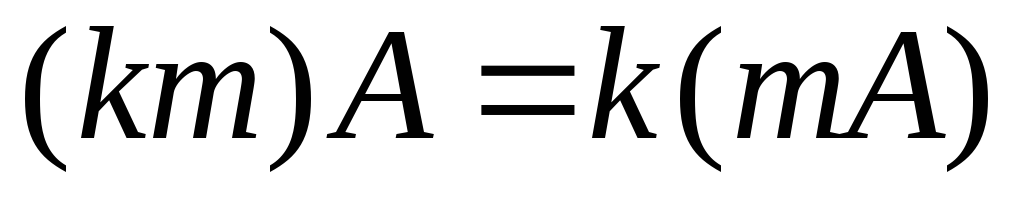 .
.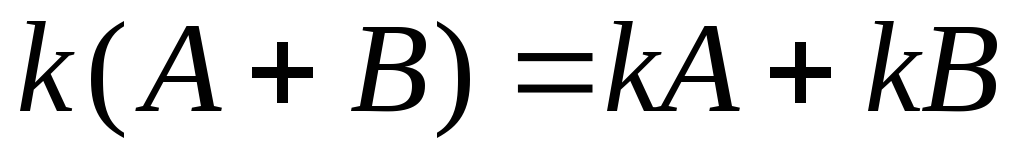 .
.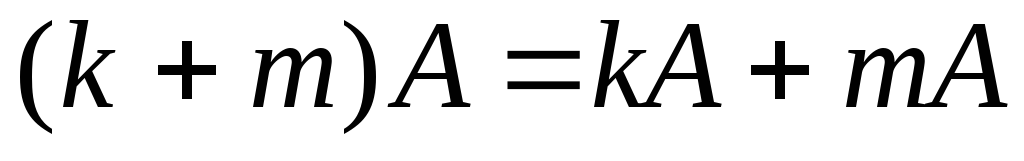 .
.
Вычитание
матриц можно
выполнить с помощью двух предыдущих
операций, т.е.
![]() .
.
Умножение
матриц.
Произведение матрицы
![]() на матрицу
на матрицу![]() (обозначается
(обозначается![]() )
определено только в том случае, когда
число столбцов матрицы
)
определено только в том случае, когда
число столбцов матрицы![]() равно числу строк матрицы
равно числу строк матрицы![]() .
В результате умножения получим матрицу
.
В результате умножения получим матрицу![]() ,
у которой столько же строк, сколько их
в матрице
,
у которой столько же строк, сколько их
в матрице![]() ,
и столько же столбцов, сколько их в
матрице
,
и столько же столбцов, сколько их в
матрице![]() .
Для удобства запоминания запишем это
кратко:
.
Для удобства запоминания запишем это
кратко:
![]()
Если
![]() ,
,![]() и
и![]() ,
то элементы
,
то элементы![]() определяются следующим образом:
определяются следующим образом:
![]() ,
(3)
,
(3)
где
![]() .
.
Итак,
произведением
матриц
![]() и
и![]() называется матрица
называется матрица![]() ,
каждый элемент которой
,
каждый элемент которой![]() равен сумме произведений элементов
равен сумме произведений элементов![]() - й строки первой матрицы (
- й строки первой матрицы (![]() )
на соответствующие элементы
)
на соответствующие элементы![]() -
го столбца второй матрицы (
-
го столбца второй матрицы (![]() ).
).
Схема вычисления:










Другими
словами, элемент ![]() является результатом
скалярного произведения
является результатом
скалярного произведения
![]() -й
вектор-строки и
-й
вектор-строки и![]() -го
вектор-столбца.
-го
вектор-столбца.
Некоторые
свойства произведения чисел не выполняются
для произведения матриц.
Заметим, что оба произведения
![]() и
и![]() можно определить лишь в том случае,
когда число столбцов матрицы
можно определить лишь в том случае,
когда число столбцов матрицы![]() совпадает с числом строк матрицы
совпадает с числом строк матрицы![]() ,
а число строк матрицы
,
а число строк матрицы![]() совпадает с числом столбцов матрицы
совпадает с числом столбцов матрицы![]() .
А именно, матрица
.
А именно, матрица![]() имеет размеры
имеет размеры![]() ,
а
,
а![]() – размеры
– размеры![]() .
При этом, вообще говоря,
.
При этом, вообще говоря,![]() (если
(если
![]() ,
то матрицы называютсяперестановочными).
Произведение двух ненулевых матриц
может равняться нулевой матрице:
,
то матрицы называютсяперестановочными).
Произведение двух ненулевых матриц
может равняться нулевой матрице:
![]() .
.
Из формулы (3) вытекают свойства умножения матриц:
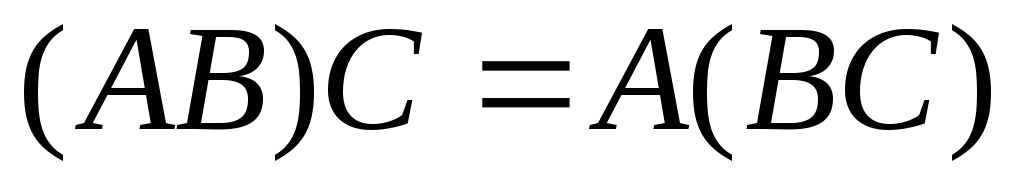 (ассоциативность
умножения);
(ассоциативность
умножения);
2)
![]() или
или![]() (дистрибутивность умножения относительно
сложения).
(дистрибутивность умножения относительно
сложения).
Легко
проверить, что для любой матрицы
![]()
![]() -го
порядка имеют место равенства
-го
порядка имеют место равенства
![]() и
и
![]() .
.
Эти
равенства показывают особую роль
единичной матрицы
![]() ,
аналогичную той роли, которую играет
число 1 при перемножении вещественных
чисел.
,
аналогичную той роли, которую играет
число 1 при перемножении вещественных
чисел.
Типовой пример
Найти:
![]() ,
если
,
если![]() =
=![]() ,
,![]() =
=![]() ,
,![]() .
.
►1)
![]() – найти нельзя, так как количество
столбцов в
– найти нельзя, так как количество
столбцов в![]() не равно количеству строк в
не равно количеству строк в![]() .
.
2)
![]() =
=![]() .
.![]() =
=![]() =
=![]() .
.
3)
![]() =
=![]()
![]() =
=
![]() =(18).
=(18).
4)
![]() =
=![]()
![]() =
=![]() =
=![]() .◄
.◄
Матрица,
полученная из данной заменой строк
столбцами с теми же номерами называется
матрицей, транспонированной
к данной и обозначается
![]() .
При транспонировании вектора-столбца
получается вектор-строка и наоборот.
.
При транспонировании вектора-столбца
получается вектор-строка и наоборот.
Операция транспонирования обладает следующими свойствами:
|
1.
|
3.
|
|
2.
|
4.
|
Типовой пример
Вычислить AB+2CT, если
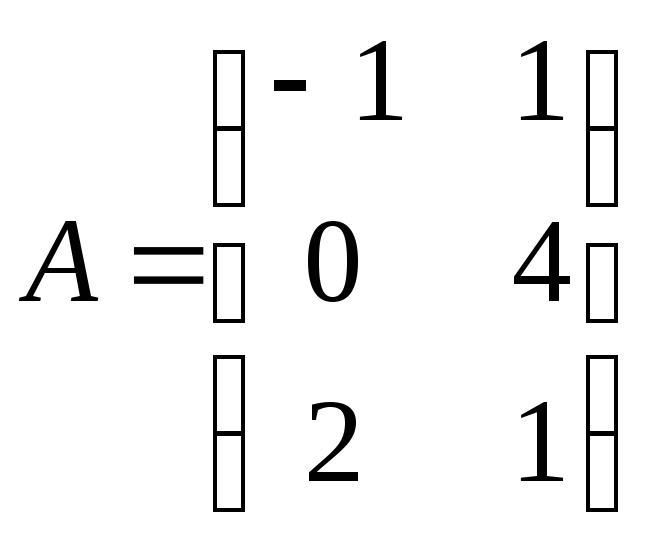 ,
,
![]() ,
,![]() .
.
►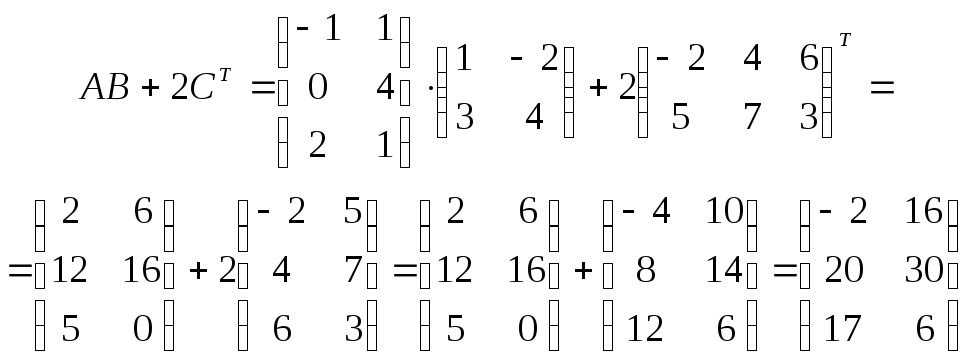 .◄
.◄
Возведение в степень возможно только для квадратных матриц.
![]() .
.
Свойства:
|
1)
|
2)
|
3)
|
4)
|
Типовой пример
►
![]() .◄
.◄
Многочлены
от матриц. Пусть
![]() - произвольная квадратичная матрица
- произвольная квадратичная матрица![]() -го
порядка,
-го
порядка,![]() -
натуральное число. Тогда
-
натуральное число. Тогда![]() -ой
степенью матрицы
-ой
степенью матрицы![]() называется произведение
называется произведение![]() матриц,
каждая из которых равна
матриц,
каждая из которых равна![]()
![]()
Нулевой
степенью
![]() квадратичной
матрицы
квадратичной
матрицы![]() называется единичная матрица:
называется единичная матрица:![]() .
Первой степенью
.
Первой степенью![]() матрицы
матрицы![]() называется сама матрица:
называется сама матрица:![]() .
.
Многочленом
степени
![]() от квадратичной матрицы называется
выражение вида
от квадратичной матрицы называется
выражение вида![]() ,
где
,
где![]() - числа.
- числа.
Типовые примеры
1.
Вычислить выражение
![]() ,
если
,
если
![]() .
.
►Выражение
![]() представляет собой матричный многочлен
представляет собой матричный многочлен
![]() ,
где
,
где
![]() - единичная матрица.
- единичная матрица.
Вычислим последовательно слагаемые этого выражения:
![]() ,
,
![]() ,
,
![]() .
.
Подставив
всё это в
![]() ,
имеем
,
имеем
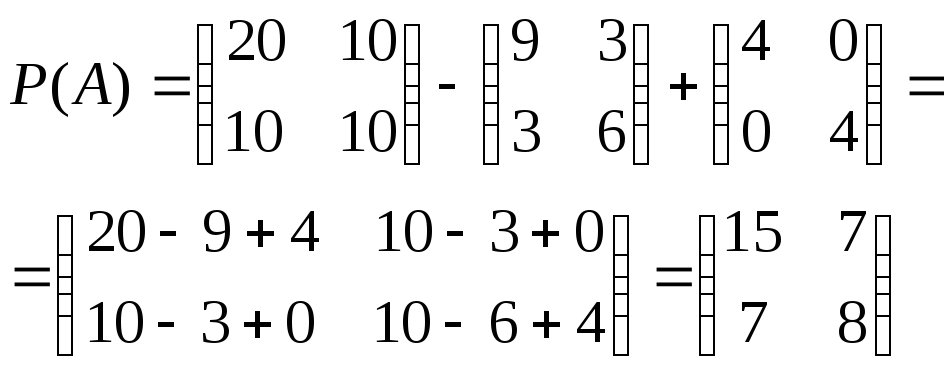 .◄
.◄
2.
Найти значение
![]() ,
если
,
если![]() .
.
►![]() ◄
◄
Пример
Данные о совокупных продажах (в тыс.руб.) некоторого торга в 1-ом и 2-м кварталах определенного года, записаны соответственно матрицами
![]() =
=
 ;
;![]() =
= .
.
Требуется записать в виде матрицы данные о совокупных продажах (в тыс. руб.) на 1-ое полугодие рассматриваемого года.
►Очевидно, искомая матрица Х является суммой двух данных матриц А и В, т.е.
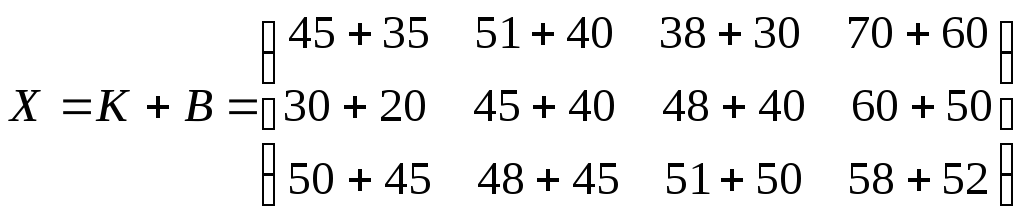 =
=
 .◄
.◄
Пример
Магазином в течение дня в розницу продано 45, 30 и 50 единиц трёх видов товаров, соответственно по ценам 1;2; 0,5 (усл. ед.). Вычислить дневную выручку от розничной продажи всех видов товаров.
►Представим
данные о проданных товарах как матрицу
![]() =
=![]() ,
а соответствующие цены (в тыс. руб) как
матрицу
,
а соответствующие цены (в тыс. руб) как
матрицу
![]() =
=
![]() .
Тогда искомую выручку
.
Тогда искомую выручку
![]() можно записать как произведение матрицы
можно записать как произведение матрицы![]() и матрицы
и матрицы![]() ,
т.е.
,
т.е.
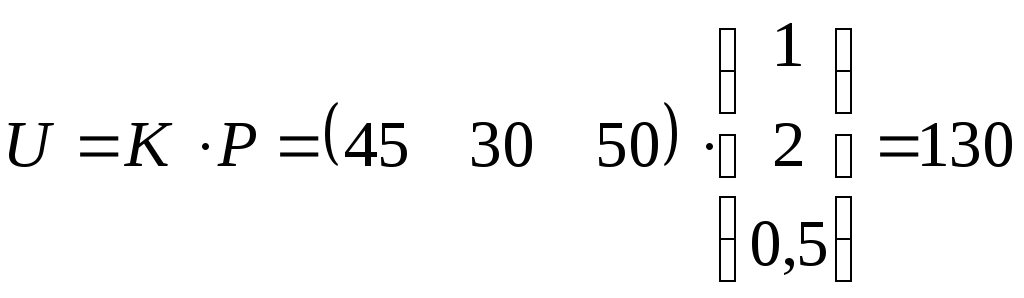 (тыс.
руб).
(тыс.
руб).
Следовательно, дневная выручка магазина от розничной продажи товара, составляет 130(тыс. руб).◄
Пример. Предположим, что указанный в предыдущем Типовой примере магазин кроме розничных, осуществляет также продажи оптовые на ярмарке и по линии посылторга. Причем данные о продажах за 1 день каждого вида товара записаны в таблице.
|
Вид продажи |
Виды товаров | ||
|
Костюм |
Пальто |
Платье | |
|
Розничная |
45 |
30 |
50 |
|
Оптовая |
38 |
25 |
40 |
|
Посылторг |
20 |
15 |
20 |
|
Цена одной ед. Товара |
1(тыс.руб) |
2(тыс.руб) |
0,5(тыс.руб) |
Требуется подсчитать дневную выручку от продаж (розничной, оптовой, посылторговской) каждого вида по отдельности. Выполнять эти вычисления с помощью матричной алгебры, предварительно переформулировав условие задачи.
►Данные о продажах (в штуках) некоторого магазина за 1 день запишем в виде матрицы:
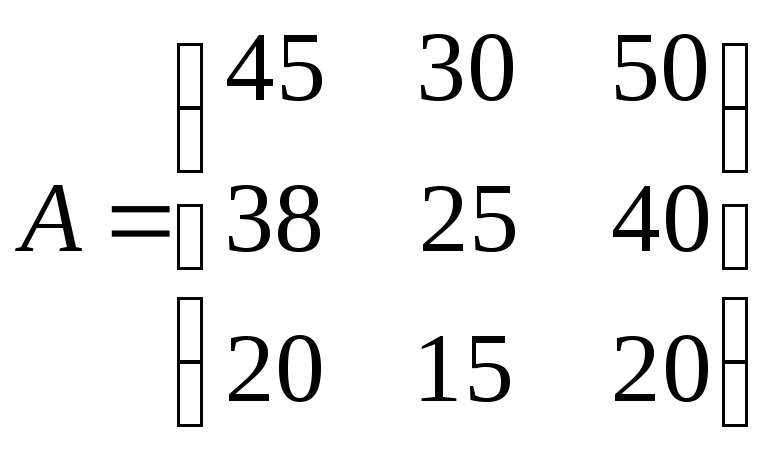 ,
,
где в строках указаны количества (в шт.) товара по видам продаж (розничная, оптовая и посылторговская), а в столбцах – количество (в шт.) по видам товаров (костюм, пальто, платье).
Данные
о ценах (в тыс. руб.) записаны матрицей-столбцом
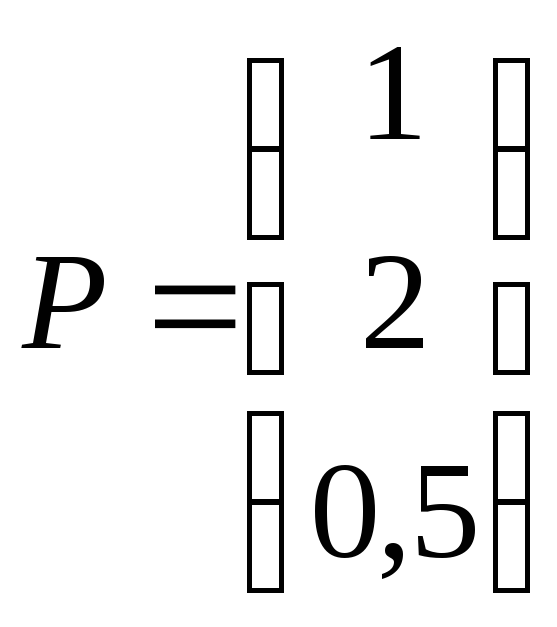 ,
элементы которой, являются ценами
соответственно первого, второго и
третьего (костюма, пальто, платья) видов
товаров.
,
элементы которой, являются ценами
соответственно первого, второго и
третьего (костюма, пальто, платья) видов
товаров.
Вычислить
дневную выручку от продажи каждого вида
товаров. Искомые дневные выручки
![]() продажи каждого из трех видов товара
можно записать в виде матрицы-столбца
продажи каждого из трех видов товара
можно записать в виде матрицы-столбца![]() и определить эту матрицу как произведение
матриц
и определить эту матрицу как произведение
матриц![]() и
и![]() следующим образом:
следующим образом:
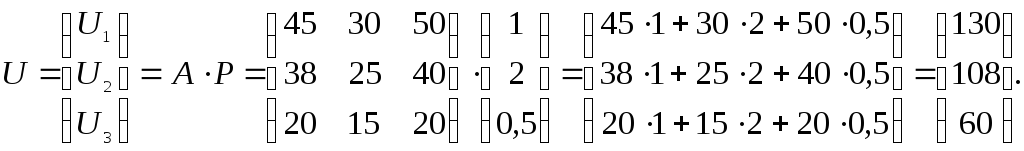
Следовательно, дневные выручки от продажи первого, второго и третьего видов товара составляют соответственно: 130, 108 и 60 (тыс.руб.).◄
Пример. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
|
Молокозавод |
Магазин | ||
|
|
М1 |
М2 |
М3 |
|
1 |
20 |
35 |
10 |
|
2 |
15 |
27 |
8 |
►Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.
![]() ,
,
![]() .
.
Тогда матрица затрат на перевозки будет иметь вид:
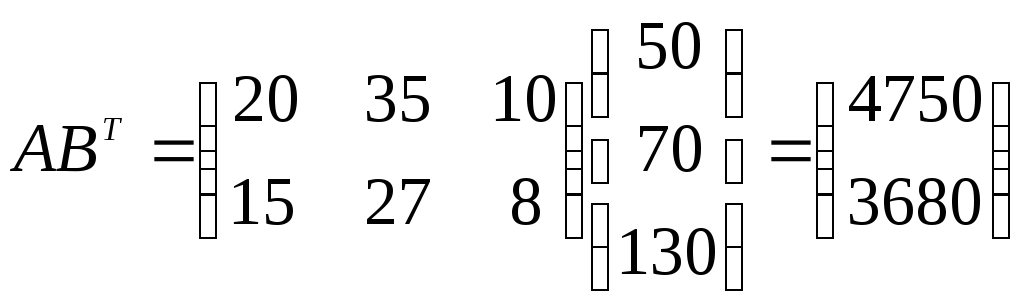 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден. ед.◄
Пример
Швейное
предприятие производит зимние пальто,
демисезонные пальто и плащи. Плановый
выпуск за декаду характеризуется
вектором
![]() .
Используются ткани четырех типов
.
Используются ткани четырех типов![]() .
В таблице приведены нормы расхода ткани
(в метрах) на каждое изделие. Вектор
.
В таблице приведены нормы расхода ткани
(в метрах) на каждое изделие. Вектор![]() задает стоимость метра ткани каждого
типа, а вектор
задает стоимость метра ткани каждого
типа, а вектор![]() - стоимость перевозки метра ткани каждого
вида.
- стоимость перевозки метра ткани каждого
вида.
|
Изделие |
Расход ткани | |||
|
|
Т1 |
Т2 |
Т3 |
Т4 |
|
Зимнее пальто |
5 |
1 |
0 |
3 |
|
Демисезонное пальто |
3 |
2 |
0 |
2 |
|
Плащ |
0 |
0 |
4 |
3 |
1. Сколько метров ткани каждого типа потребуется для выполнения плана?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
►Обозначим
через
![]() матрицу, данную нам в условии, т. е.
матрицу, данную нам в условии, т. е.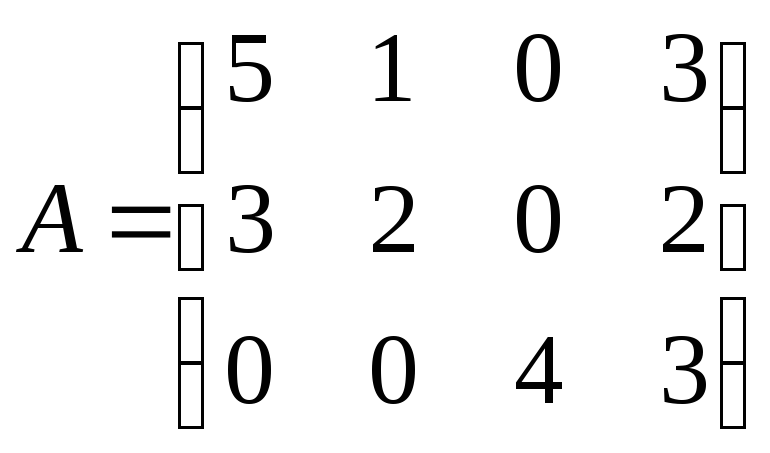 ,
,
тогда
для нахождения количества метров ткани,
необходимой для выполнения плана, нужно
вектор
![]() умножить на матрицу
умножить на матрицу![]() :
:

Стоимость
ткани, расходуемой на пошив изделия
каждого вида, найдем, перемножив матрицу
![]() и вектор
и вектор![]() :
:
 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
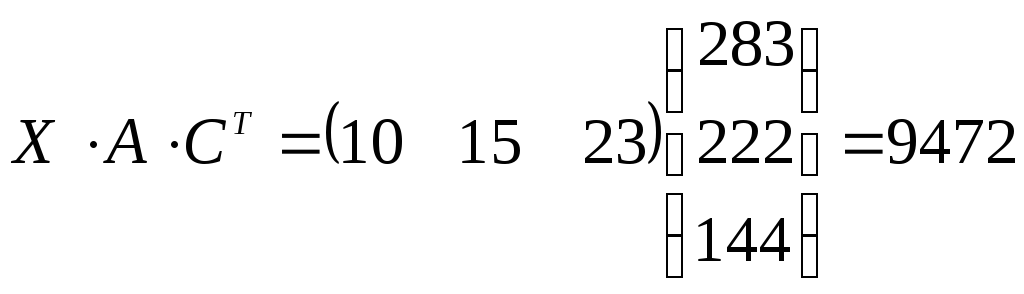 .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
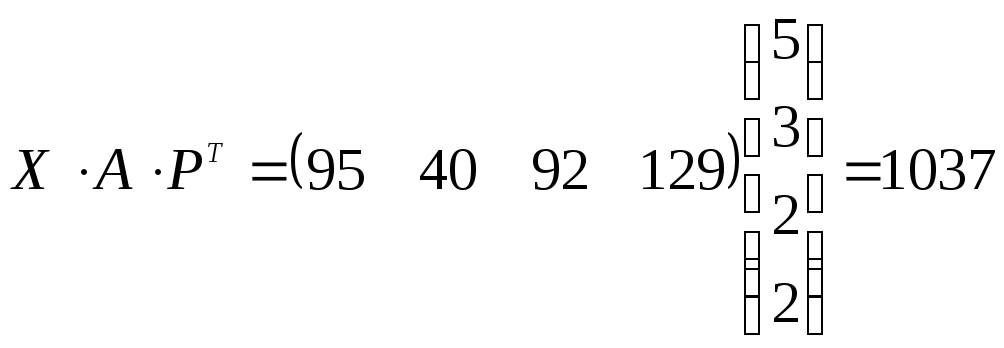 .
.
Итак,
![]() (ден. ед).◄
(ден. ед).◄
Пример
Имеется 4 предприятия, выпускающие 3 вида изделий и использующие при производстве 2 вида сырьевых материалов. Данные о дневной производительности предприятия по каждому изделию (число изделий в день) и о затратах сырья на 1ед изделия (кг/шт), а также число дней работы каждого предприятия и стоимость в руб. кг сырья каждого вида, даны в таблице.
|
Изделия |
Производительность в шт/день |
Затраты кг/шт | ||||
|
1 |
2 |
3 |
4 |
I |
II | |
|
|
7 |
10 |
3 |
0 |
5 |
12 |
|
|
5 |
7 |
2 |
0 |
10 |
4 |
|
|
0 |
4 |
8 |
4 |
6 |
8 |
|
|
Кол-во раб. дней в году |
Цены ед. сырья | ||||
|
100 |
120 |
50 |
200 |
30 |
20 | |
Требуется определить (записав с помощью операций над матрицами):
cуммарную производительность (за весь рабочий период) каждого предприятия по каждому из изделий.
количество каждого вида сырья, необходимого на каждом предприятии и для всех четырех предприятий.
размеры кредитов, которые необходимо предоставить всем предприятиям на закупку сырья.
►Прежде всего запишем условие задачи в матричном виде. Пусть матрица
![]() –матрица
производительности,
–матрица
производительности,
![]() –
матрица затрат сырья и матрица
–
матрица затрат сырья и матрица![]() -
-
матрица цен, тогда
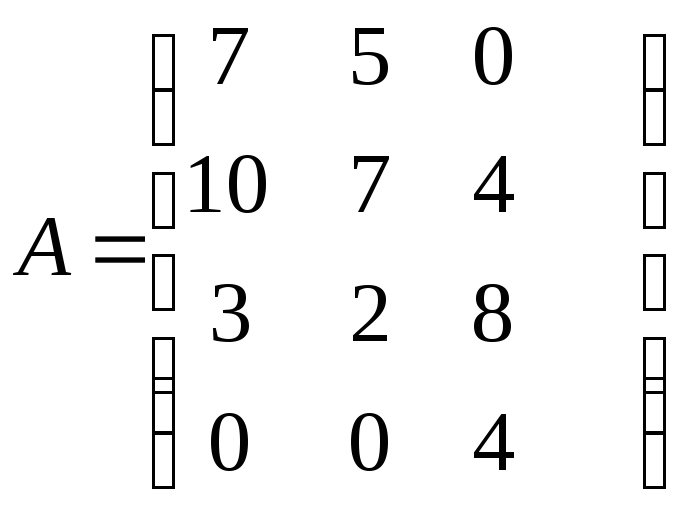 ;
;
 ;
;
![]() .
.
Для расчета суммарной производительности используем запись времени работы каждого из предприятий в виде диагональной матрицы
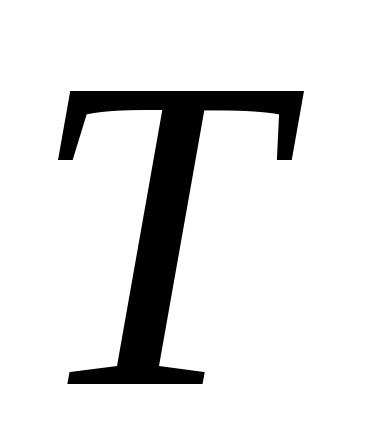
 .
.
