31. Функционально полные и функционально замкнутые системы булевых функций.

Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булефых функций (f₁, f₂, ... f_k), что произвольная булева функция f может быть записана в виде формулы через функции этой совокупности.

Перечислим предполные классы булевых функций:

1. булевы функции, сохраняющие константу 0;

2. булевы функции, сохраняющие константу 1;

3. самодвойственные булевы функции;

4. линейные булевы функции;

5. монотонные булевы функции;

Замкнутый класс в теории булевых функций — такое множество функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: . Другими словами, любая функция, которую можно выразитьформулой с использованием функций множества , снова входит в это же множество.

Особо важны для теории булевых функций следующие замкнутые классы, называемые предполными классами:

• Класс функций, сохраняющих константу 0:.

• Класс функций, сохраняющих константу 1:.

• Класс самодвойственных функций: .

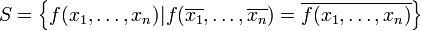• Класс монотонных булевых функций: .

• Класс линейных булевых функций: .

32 Полиномы Жегалкина. Метод неопределенных коэффициентов построения полиномов Жегалкина. Примеры.

: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие. Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере.

Пример. Найти полином Жегалкина для функции заданной векторно: 

 f( x,y )  =  ( 0, 1, 1, 0 ).

Составим  таблицу 1.14 задания данной функции.

Таблица 1.14

x	y	f
0	0	0
0	1	1
1	0	1
1	1	0

Полином Жегалкина для функции двух переменных ищем в следующем виде:

f( x, y )  =  a0 a1·xa2·ya3·xy                                  (1.6)

Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14.

            Подставляя набор переменных(0,0) в (1.6) получим: 

a = 0.

            Аналогично для набора  (0,1) получим:

.  a = 1

34.

Классы и их функциональная замкнутость. Метод определения принадлежности булевой функции классу линейных функций. Примеры.

Замкнутый класс в теории булевых функций — такое множество функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: . Другими словами, любая функция, которую можно выразитьформулой с использованием функций множества , снова входит в это же множество.

Множество всех возможных булевых функций замкнуто.

Особо важны для теории булевых функций следующие замкнутые классы, называемые предполными классами:

• Класс 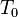функций, сохраняющих константу 0: .

• Класс функций, сохраняющих константу 1: .

• Класс самодвойственных функций: .

• Класс монотонных булевых функций: .

• Класс линейных булевых функций:

Булева функция называется линейной, если существуют такие, где, что для любыхимеет место равенство:

.