
Урав прямой каз
.docx-
6х-2у-8=0 түзуiне перпендикуляр түзудiң теңдеуi:
А) у=3х-9.
В) 2х-5у-8=0.
С)
+у=-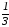 х-10.
х-10.
D) 2у=8-х.
Е)
у=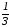 х-8.
х-8.
-
у=х-20 теңдеуiне перпендикуляр (-2; 3) нүктесi арқылы өтетiн түзудiң теңдеуi:
А)+у-3=-(x+2).
В) 2х-5у-8=0.
С) 2у=6х-8.
D) 2у=8-6х.
Е) 7х+5у-1=0.
-
2x+y=3 және х-у=0 түзулерiнiң қиылысу нүктесi:
А) +М(1; 1) .
В) М(3; -1) .
С) М(0; 0) .
D) М(-3; -1) .
Е) М(-6; 2) .
-
Координата бас нүктесi О мен А(-6; 2) нүктесiн қосатын ОА кесiндiнiң ортасы болатын М нүктесiнiң координатасы:
А) +М(-3; 1) .
В) М(3; -1) .
С) М(0; 0) .
D) М(-3; -1) .
Е) М(-6; 2) .
-
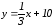 түзуiнiң
жалпы теңдеуі:
түзуiнiң
жалпы теңдеуі:
А) +х-3у+30=0.
В) 2х-5у-8=0.
С)
у=-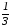 х-10.
х-10.
D) 2у=8-6х.
Е)
у=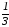 х-8.
х-8.
-
Оу осiне параллель және Ох осiн ұзындығы 4-ке тең кесiндiде қиятын түзудiң теңдеуi:
А) +х=4.
В) у=0.
С) у=-4.
D) х=-4.
Е) х=0.
-
Ох осiне параллель және Оу осiн ұзындығы 14-ке тең кесiндiде қиятын түзудiң теңдеуi:
А) +у=14.
В) у=0.
С) у=-4.
D) х=-4.
Е) х=0.
-
2х-3у=6 түзуiнiң k және b параметрлерi:
А)
к=-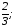 в=0.
в=0.
В)
+к=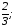 в=-2.
в=-2.
С)
к=-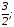 в=0.
в=0.
D)
к=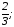 в=1.
в=1.
Е)
к=-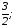 в=1.
в=1.
-
2х-у-2=0 түзуiнiң абсцисса осiмен қиылысу нүктесi:
А) М(1; 2) .
В) М(2; 4) .
С) М(0; 2) .
D) М(1; 4) .
Е) +М(1; 0) .
-
Екiншi реттi қисықтың жалпы теңдеуi:
А)Ax+By+C=0.
В) у=kx+b.
С) +Ax2+Bхy+Cу2+Dx+Ey+F=0.
D)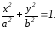
Е)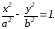
-
А(х1;у1) және В(х2;у2) берiлген. АВ кесiндiсiнiң ұзындығын есептеңiз:
A)+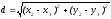 ;
;
B)
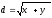 ;
;
C)
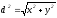 ;
;
D)
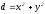 ;
;
E)
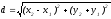 .
.
-
А(2; 4) және В(5;8) берiлген. АВ кесiндiсiнiң ұзындығын есептеңiз:
A) +5;
B) 25;
C) 1;
D) -7;
E) -12.
-
В=0, С
 0
болғанда, Ах+Ву+С=0
түзу қалай
орналасады:
0
болғанда, Ах+Ву+С=0
түзу қалай
орналасады:
A) ОХ осiне сәйкес
B) +ОУ осiне параллель
C) ОХ осiне параллель
D) ОУ осiне сәйкес
E) Координаттар басынан өтедi
-
2,5у-5х+5=0 түзуiнiң бұрыштық коэффициенттерi:
A) -2;
B) 2,5;
C)+ 2;
D) -2,5;
-
5.
-
А=0, С
 0
болғанда, Ах+Ву+С=0
түзу қалай
орналасады:
0
болғанда, Ах+Ву+С=0
түзу қалай
орналасады:
A) ОХ осiне сәйкес
B) ОУ осiне параллель
C) +ОХ осiне параллель
D) ОУ осiне сәйкес
E) Координаттар басынан өтедi
-
Ох осімен 2х+3у-6=0 түзуiнiң қиылысу нүктесi:
A)(0;-2).
B)(0;2).
C)(-3;0).
D)+(3;0).
E)(0;3).
-
Оу осiмен 3х-4у+12=0 түзуiнiң қиылысу нүктесi:
A)+(0;3).
B)(0;-3).
C)(3;0).
D)(4;0).
E)(-4;0).
-
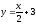 түзуiне
параллель түзудiң
бұрыштық коэффициентi... тең.
түзуiне
параллель түзудiң
бұрыштық коэффициентi... тең.
-
-2
-
2
-
3
-
+
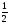
-
-
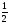
-
у=-2х+7 түзуiне перпендикуляр түзу:
-
у=2х+3
-
у=-2х-1
-
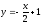
-
+
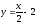
-
у=-3х-1
-
Бұрыштық коэффициентiмен берiлген түзудiң теңдеуi:
А)
+ .
.
В)
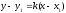 .
.
С)
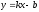 .
.
D)
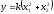 .
.
Е)
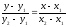 .
.
-
М(х1,у1) нүктесінен Ах+Ву+С=0 түзуiне дейiнгi ара қашықтықты есептеу формуласы:
A)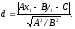
B)
+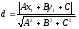
C)
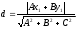
D)
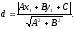
E)
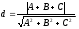
-
а және в қандай мәндерiнде ах-2у-1=0, 6х-4у-в=0 түзулерi параллель болады:
A)
+а=3,
в 2.
2.
B) а=2, в=2.
C) а=3, в=2.
D)
а=
-3, в![]() 2.
2.
E)
а=6,
в![]() 6.
6.
-
а және в қандай мәндерiнде у = ах+2, у = 5х-в түзулерi параллель болады:
A)
а=
-1/5, в![]() -2.
-2.
B) а= -1/5, в= -2.
C) а= -5, в= -2.
D)
+а=
5, в![]() -2.
-2.
E)
а![]() 5,
в= -2.
5,
в= -2.
-
A=0 болғанда, Ах+Ву+С=0 түзу қалай орналасады:
A) ОХ осiне сәйкес
B) ОУ осiне параллель
C) +ОХ осiне параллель
D) ОУ осiне сәйкес
E) Координаттар басынан өтедi
-
A=C=0 болғанда, Ах+Ву+С=0 түзу қалай орналасады:
A) +ОХ осiне сәйкес
B) ОУ осiне параллель
C) ОХ осiне параллель
D) ОУ осiне сәйкес
E) Координаттар басынан өтедi
-
B=C=0 болғанда, Ах+Ву+С=0 түзу қалай орналасады:
A) ОХ осiне сәйкес
B) ОУ осiне параллель
C) ОХ осiне параллель
D) +ОУ осiне сәйкес
E) Координаттар басынан өтедi
-
2х-6у+3z-12=0 жазықтығының нормаль векторын көрсетiңiз:
-
(2; 6; 3).
-
(2; 6; -12).
-
+(2; -6; 3).
-
(2; 6; 3;-12).
-
(-2; 6; -3).
-
Жазықтықтың жалпы теңдеуi:
-
Ax+By+C=0.
-
у=kx+b.
-
Ax2 +Bхy+Cу2 +Dx+Ey+F=0.
-
x2\a2 -y2\b2=1.
-
+Ax+By+Cz+D=0.
-
Кеңiстiкте түзу теңдеуiнiң параметрлiк түрде берiлуi:
-
A(x-x0)+B(y-y0)+ C(z-z0)=0.
-
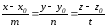 .
. -
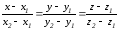 .
. -
у=kx+b.
-
+
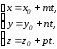
-
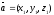
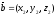 берілген.
берілген.
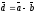 векторының координатасын
табыңыз:
векторының координатасын
табыңыз:
A)
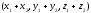
B)
+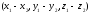
C)
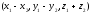
D)
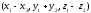
E)
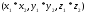
-
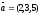 және
және
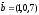 берілген.
берілген.
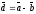 векторының координатасын
табыңыз:
векторының координатасын
табыңыз:
A) (3,3,12).
B) (1,3,2).
C) +(1,3,-2) .
D) (-1,-3,2).
E) (2,0,35).
-
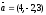 және
және
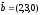 берілген.
берілген.
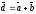 векторының координатасын
табыңыз:
векторының координатасын
табыңыз:
A) (6,-1,3).
B) (8,-6,0).
C) (-2,5,-3) .
D) (2,5,3).
E) +(6,1,3).
-
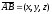 векторының ұзындығын
анықтайтын формула:
векторының ұзындығын
анықтайтын формула:
A)
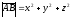 .
.
B)
+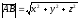 .
.
C)
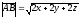 .
.
D)
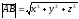 .
.
E)
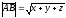 .
.
-
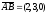 векторының ұзындығы:
векторының ұзындығы:
A)
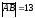 .
.
B)
+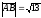 .
.
C)
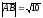 .
.
D)
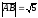 .
.
E)
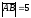 .
.
-
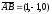 векторының ұзындығы:
векторының ұзындығы:
A)
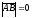 .
.
B)
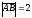 .
.
C)
+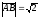 .
.
D)
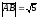 .
.
E)
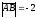 .
.
-
 және
және
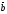 векторларының
скаляр көбейтiндiсiнiң
формуласы:
векторларының
скаляр көбейтiндiсiнiң
формуласы:
A)
+( ,
,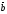 )=
)=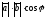 .
.
B)
( ,
,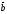 )=
)=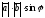 .
.
C)
( ,
,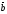 )=
)=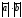 .
.
D)
( ,
,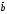 )=
)=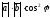 .
.
E)
( ,
,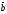 )=
)=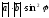 .
.
-
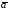 =(х1,х2,х3)
және
=(х1,х2,х3)
және
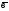 =(у1,у2,у3)
векторларының
перпендикуляр болуының
шарты:
=(у1,у2,у3)
векторларының
перпендикуляр болуының
шарты:
-
+x1* y1 + x2*y2 +…+xn yn =0.
-
(x1 + x2 +xn)*(y1 +y2 +yn)=0
-
x1* y1 +x2*y2 -…-xn yn =0
-
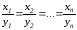
-
x1* y1 + x2*y2 +…+xn yn =1.
-
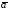 =(4,-2,-4)
және
=(4,-2,-4)
және
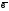 =(6,-3,2)
векторларының скаляр көбейтiндiсi:
A)23.
B)24.
C)
+22.
D)21.
=(6,-3,2)
векторларының скаляр көбейтiндiсi:
A)23.
B)24.
C)
+22.
D)21.
E)20.
-
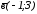 векторының
ұзындығын табыңыз:
векторының
ұзындығын табыңыз:
A) 2.
B)
4.
C) +
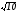 .
D)
.
D)
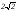 .
E)
.
E)
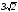 .
.
-
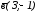 векторының
ұзындығын табыңыз.
векторының
ұзындығын табыңыз.
A) 2.
B) +
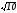 .
C)
.
C)
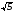 .
.
D) 3.
E)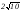 .
.
-
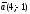 ,
,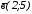 векторлары берілсін.
векторлары берілсін.
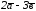 векторының координатасын табыңыз:
векторының координатасын табыңыз:
A) (-2; -16). B) (-6; 14). C) (-6; -15). D) (6;15). E) + (2;-17).
-
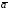 (х;
2) және
(х;
2) және
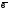 (1;-3)
векторлары х-тің қандай мәнінде
коллинеар болады?
(1;-3)
векторлары х-тің қандай мәнінде
коллинеар болады?
A) 2/3. B)+-2/3. C)-6. D)6. E)-1.
-
Скалярлық шама:
А) параметр.
B) Күш.
C) Жылдамдық.
D)+ Уақыт.
E) вектор
-
Векторлық шама:
А) Аудан.
B) + Күш.
C) сан.
D) Уақыт.
E) Масса.
-
Векторлардың қосындысының геометриялық мағынасы:
А) +үшбұрыш;
B) тiкбұрыш;
C) Квадрат.
D) ромб.
E) Трапеция.
-
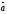 векторының
санына
көбейтiлген,
векторының
санына
көбейтiлген,
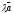 векторының бағыты
векторының бағыты
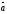 ,
векторының бағытына
бағыттас болады, егер:
,
векторының бағытына
бағыттас болады, егер:
А) =0.
B) +>0.
C) <0.
D) =1.
E) 0.
-
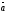 векторының
санына
көбейтiлген,
векторының
санына
көбейтiлген,
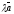 векторының бағыты
векторының бағыты
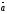 ,
векторының бағытына
қарама-қарсы
болады, егер:
,
векторының бағытына
қарама-қарсы
болады, егер:
А) =0.
B) >0.
C) +<0.
D) =1.
E) 0.
48.
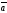 және
және
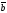 векторларының скаляр көбейтіндісі неге
тең:
векторларының скаляр көбейтіндісі неге
тең:
A)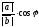
B)|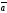 ||
||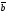 |
|
C)|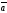 ||
||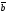 |tg
|tg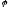
D)|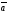 ||
||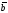 |sin
|sin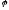
+E)| ||
||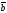 |cos
|cos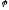
49.
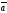 и
и
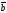 векторларының көбейтіндісі нөльге тең
болады, егер:
векторларының көбейтіндісі нөльге тең
болады, егер:
A)
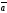 =
=
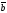
B)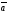 ||
||
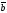
C)
+
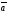
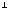
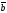
D)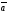 =-
=-
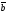
E)|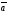 |=|
|=|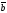 |=1
|=1
50.
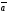 =(x1,
y1,z1)
и
=(x1,
y1,z1)
и
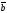 =(x2,
y2, z2)
векторлар үшін x1x2+y1
y2+z1z2
формуласы
=(x2,
y2, z2)
векторлар үшін x1x2+y1
y2+z1z2
формуласы
неге тең:
A)+
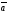
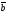
B)
пр
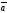
C)
пр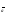
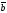
D)
соs(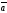
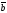 )
)
E)
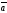 х
х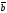
51.
A(1;2;3) және B(3;-4;6)
нүктелері берілген.
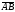 векторының ұзындығын анықтаңдар:
векторының ұзындығын анықтаңдар:
A) 6
B)
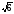
C) 1
D) + 7
E) 3
52.
Егер
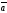 векторының x=4, y=
-12 екі координатасы және вектордың
ұзындығы
векторының x=4, y=
-12 екі координатасы және вектордың
ұзындығы
|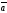 |=13
белгілі болса , онда үшінші координатасы
неге тең :
|=13
белгілі болса , онда үшінші координатасы
неге тең :
A)+
 3
3
B)
 4
4
C) 3
D)
 2
2
E) 5
53.
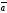
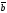 -ны
табу керек, егер |
-ны
табу керек, егер |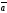 |=3,
|
|=3,
|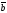 |=4,
|=4,
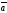

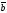 =
=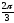 берілген болса:
берілген болса:
A) 6
B) -5
C) 4
D) + –6
E) 5
54.
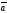 =(x1,
y1, z1)
және
=(x1,
y1, z1)
және
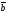 =(x2,
y2, z2)
векторлар үшін
=(x2,
y2, z2)
векторлар үшін
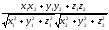 мына
мына
формула нені анықтайды:
A)
пр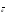
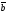
B)
пр
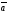
C)
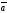
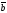
D)
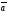 х
х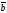
E)
+ соs(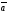

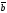 )
)
55.
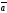 =
(1;1;0) және
=
(1;1;0) және
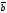 =
(1;0;1) векторларының арасындағы бұрышты
табу керек:
=
(1;0;1) векторларының арасындағы бұрышты
табу керек:
A)+ 600
B) 450
C) 0
D) 300
E) 900
56.
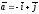 және
және
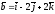 векторларының арасындағы бұрышты табу
керек:
векторларының арасындағы бұрышты табу
керек:
A) 450
B) + 1350
C) 600
D) 300
E) 900
57.
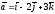 және
және
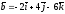 берілген болса, олар:
берілген болса, олар:
A)
|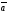 |=2,
|
|=2,
|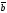 |
| 0
0
B)
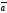
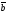
C)
+
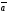 ||
||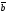
D)
|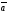 |=1,
|
|=1,
|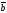 |=2
|=2
E)
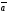 х
х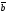 =0
=0
58.
Мына векторлар
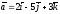 және
және
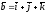 қалай орналасқан:
қалай орналасқан:
A)
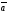 ||
||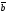
B)
|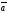 |=1,
|
|=1,
|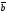 |=2
|=2
C)
|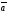 |=2,
|
|=2,
|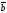 |
| 0
0
D)
+
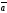
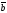
E)
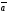 х
х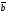 =0
=0
59.
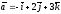 жане
жане
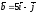 векторларының скаляр көбейтіндісін
табыңдар.
векторларының скаляр көбейтіндісін
табыңдар.
A) 0
B) + –7
C) 1
D) –4
E) 5
60.
Егер
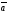 =(1,1,0),
=(1,1,0),
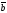 =(1,0,1),
пр
=(1,0,1),
пр
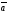 -ны
табыңдар
-ны
табыңдар
A) 2
B)
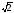
C)
+
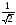
D) 0
E) 1
61. Бағыттаушы косинустардың квадраттарының қосындысы неге тең болады
A)+ 1
B) 2
C) 0
D)
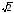
E)
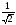
62. A(-3,7) және B(5,11) екі нүкте берілген. AВ кесіндісінің орта нүктесінің
координаталарын табыңыз:
A) (-9,-1)
B) (9,1)
C)(-1,9)
D) + (1,9)
E) (4,2)
63.
 және
және
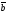 векторлары бойынша салынған параллелограмның
ауданы тең :
векторлары бойынша салынған параллелограмның
ауданы тең :
A)
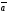 +
+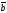
B)
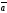 х
х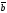
C)
|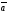 |х|
|х|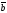 |
|
D)
|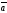 |х|
|х|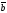 |cos
|cos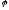
E)
+ |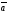 х
х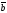 |
|
64.
Егер
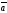 ,
,
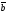 ,
,
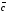 векторлары компланар болса, онда:
векторлары компланар болса, онда:
A)
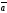 х
х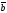 =0
=0
B)
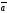 х
х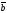 =0
=0
C)
+
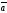
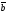
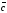 =0
=0
D)
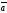
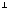
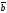
E)
(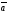 +
+
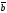 )
)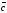 =0
=0
65.
Егер |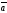 |=3,
|
|=3,
|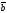 |=4,
|=4,
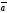

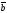 =
= берілген болса, |
берілген болса, |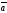 х
х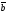 |
табу керек:
|
табу керек:
A) 12
B)
+ 6![]()
C) 7
D) 6
E)
7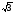
66.
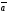 =(x1,
y1, z1),
=(x1,
y1, z1),
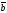 =(x2,
y2, z2)
,
=(x2,
y2, z2)
,
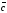 =(x3,
y3, z3)
векторлар үшін мына
=(x3,
y3, z3)
векторлар үшін мына
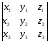
формула нені анықтайды:
A)+
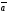
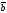
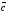
B)
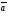
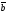
C)
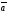 х
х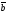
D)
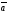 х
х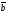
E)
(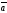 х
х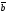 )х
)х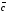
67.
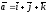 және
және
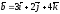 векторларының векторлық көбейтіндісін
табыңдар:
векторларының векторлық көбейтіндісін
табыңдар:
A)
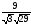
B)
+
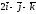
C)
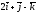
D)
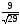
E)
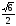
68.
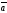 және
және
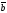 векторларының векторлық көбейтіндісі
қандай жағдайда нөльге тең болады:
векторларының векторлық көбейтіндісі
қандай жағдайда нөльге тең болады:
A)
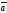
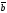
B)
|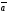 |=|
|=|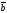 |=1,
|=1,
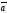
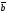
C)
|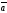 |=|
|=|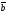 |=3,
|=3,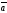
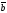
D)
|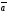 |=|
|=|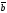 |=2,
|=2,
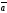
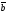
E)
+
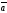 ||
||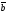
69.
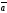 =(x1,
y1, z1)
және
=(x1,
y1, z1)
және
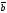 =(x2,
y2, z2)
болса, онда мына анықтауыш
=(x2,
y2, z2)
болса, онда мына анықтауыш
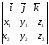
нені анықтайды:
A)
пр
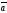
B)
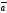 ||
||
C)
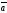
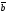
D)
+
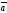 х
х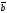
E)
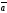
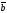
70.
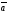 =(1,2,3),
=(1,2,3),
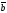 =(0,2,-1),
=(0,2,-1),
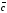 =
(-2,1,0) векторлары бойынша тұрғызылған
параллелепипедтің көлемін табыңдар:
=
(-2,1,0) векторлары бойынша тұрғызылған
параллелепипедтің көлемін табыңдар:
A) 0
B) 10
C) + 17
D) 7
E) 2
71.
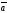 =(1,2,3),
=(1,2,3),
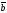 =(-2,3,4),
=(-2,3,4),
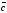 =
(-1,5,7) векторлар қалай орналасқан:
=
(-1,5,7) векторлар қалай орналасқан:
A)
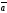 ||
||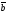
B)
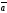
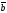
C)
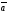 ||
||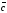
D) + компланар
E) компланар емес
72. A(х1,у1) және B(х2,у2) нүктелері арқылы өтетін түзудің теңдеуі:
A)+
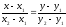
B) y-y1=k(x-x1)
C) y=kx+b
D)
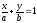
E)
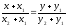
73. L1: y = k1x+b1 және L2: y = k2х+b2 түзулері параллель, егер:
A) k1+k2=1
B) k1k2 = -1
C) k1k2 =1
D) k1 = - k2.
E) + k1= k2
74. L1: y = k1x+b1 және L2: y = k2х+b2 түзулері перпендикуляр, егер:
A) k1+k2=1
B) k1= k2
C) k1k2 =1
D) k1 = - k2.
E) + k1k2 = -1
75. Бұрыштық коэффициент арқылы берілген түзудің теңдеуі:
A)
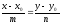
B)
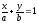
C) + y=kx+b
D) x=x1+tl, y=y1+tm
E)
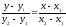
76. A(1;-3) және B(4;-2) нүктелері арқылы өтетін түзудің теңдеуін табыңдар:
A)+ x - 3y =10
C) x - 3y = 7
D) x+3y=8
B) x+3y =10
E) x-5y =10
77.
(1;-3) нүктесі арқылы
өтетін,
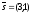 векторына параллель
болатын түзудің
векторына параллель
болатын түзудің
теңдеуін табыңдар:
A) х+3у=8
B) х+3у=10
C) х-3у=7
D) х-3у=8
E) + х-3у=10
78.
Егер
 - L1:y=k1x+b1
және L2:
y=k2x+b2
түзулерінің арасындағы бұрыш болса,
онда мына
- L1:y=k1x+b1
және L2:
y=k2x+b2
түзулерінің арасындағы бұрыш болса,
онда мына
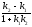 формула
нені анықтайды:
формула
нені анықтайды:
A)
cos
B)
+ tg
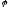
C)
sin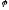
D)
ctg
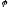
E)
cosec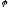
79. A(4;3) нүктесінен 3х+4у-10=0 түзуіне дейінгі арақашықтықты табыңдар:
A) 5
B) 3
C) + 2,8
D) 4,8
E) 2,4
80. 5х-у+7=0 және 3х+2у+9=0 түзулерінің арасындағы бұрышын табыңдар:
A) 900
B) 300
C) 600
D) + 450
E) 00
81. 5х+2у-3=0 түзуге перпендикуляр болатын түзудің бұрыштық коэффициентін
табыңдар:
A)+
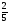
B)
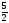
C)
-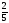
D)
-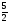
E) 5
82. (-1;2) нүктесі арқылы өтетін, 2х-3у+7=0 түзуге параллель болатын түзудің
теңдеуін табыңдар :
A)+ 2х-3у+ 8=0
B) 2х+3у- 4=0
C) 3х -2у -1=0
D) 3х+3у- 8=0
E) 2х+3у- 8=0
83. A(-1;3;2) нүктеден 2х+2у-z+3=0 жазықтыққа дейінгі қашықтықты табыңдар:
A) 2
B) + 5/3
C) 3
D) 2/3
E) 1
84. Кеңістіктегі түзудің канондық теңдеуі:
A) Ax1+By1+Cz1=0
B) x=x1+tl, y=y1+tm, z=z1+tn
C)
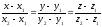
D)
+
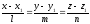
E) Ax1+By1+Cz1 +D=0
