1. Прямоугольные изометрические проекции

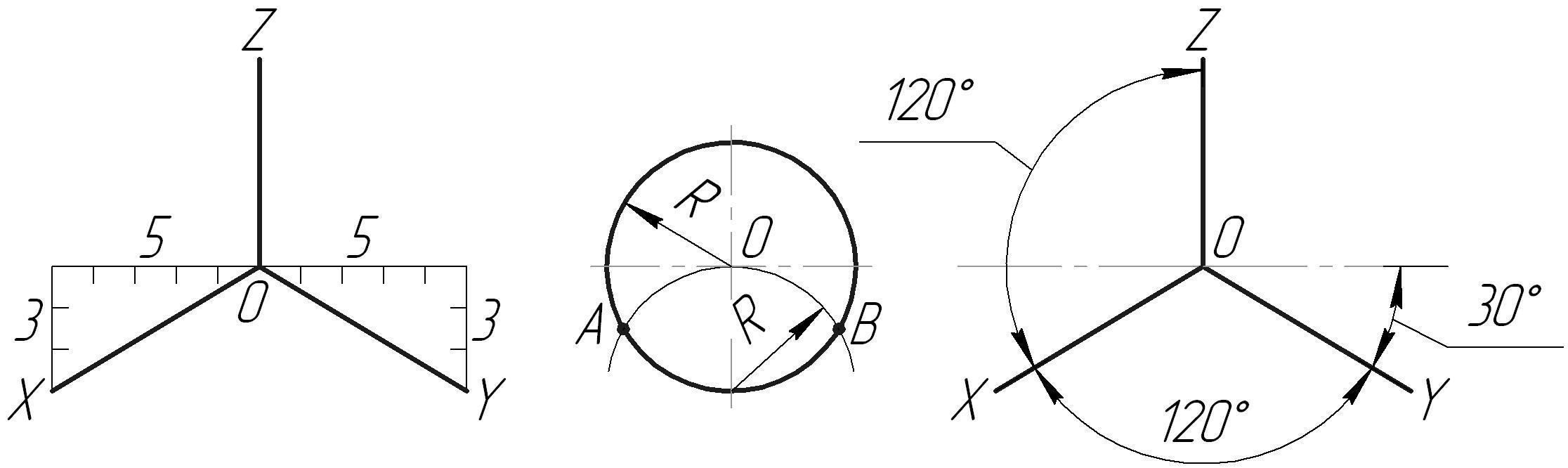
Прямоугольной изометриейназывается аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.

а) б) в)

Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.

При практических построениях коэффициент искажения (К) по аксонометрическим осям согласно ГОСТ 2.317- 2011 рекомендуют равный единице. При этом изображение получают более крупным по сравнению с теоретическим или точным изображением при коэффициентах искажения 0,82. Увеличение равно 1,22. На рис. 2 приведён пример изображения детали в прямоугольной изометрической проекции.

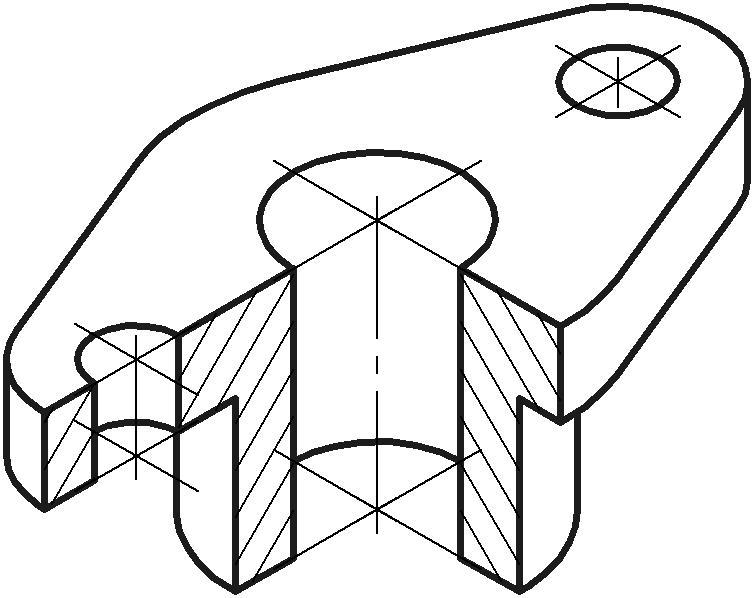
Рис. 2. Изометрия детали.

1. Построение в изометрии плоских фигур

Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П₁).

а) Строим изометрические оси (рис.3).

б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О₀ по осям откладываем натуральные величины отрезков: А₀О₀ = АО; О₀D₀ = ОD; К₀О₀ = КО; О₀Р₀ = ОР.

в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.

В нашем примере стороны ВС и FЕ параллельны оси Х.

В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В₀С₀ = ВС; F₀Е₀= FЕ.

г) Соединяя полученные точки, получим изометрическое изображение шестиугольника в плоскости Н (П₁).

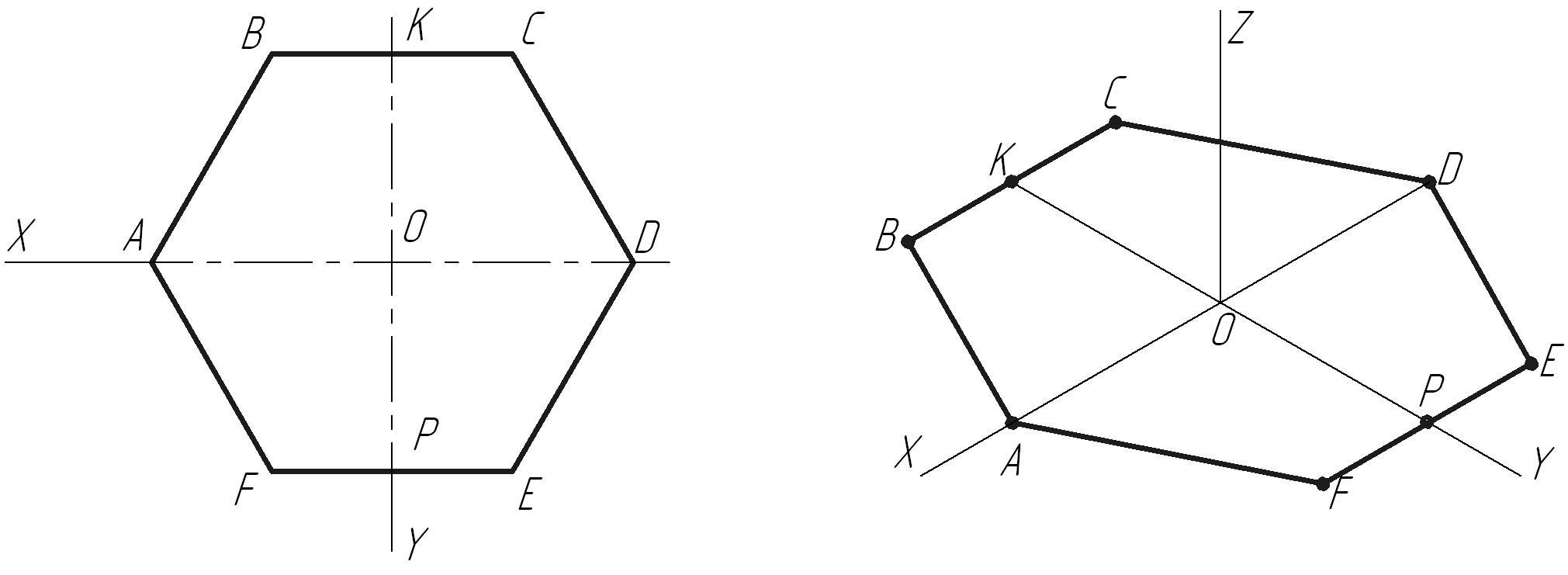
Рис. 3. Изометрическая проекция шестиугольника на чертеже

и в горизонтальной плоскости проекции

На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.

Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.

На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.

Рис. 4 Изометрическое изображение плоских фигур

а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскостиW.

Для прямоугольной аксонометрии любого вида правило определения главных осей эллипса овала, в который проецируется окружность, лежащая в какой-либо плоскости проекции, может быть сформулировано следующим образом: большая ось овала располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая совпадает с направлением этой оси. Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.

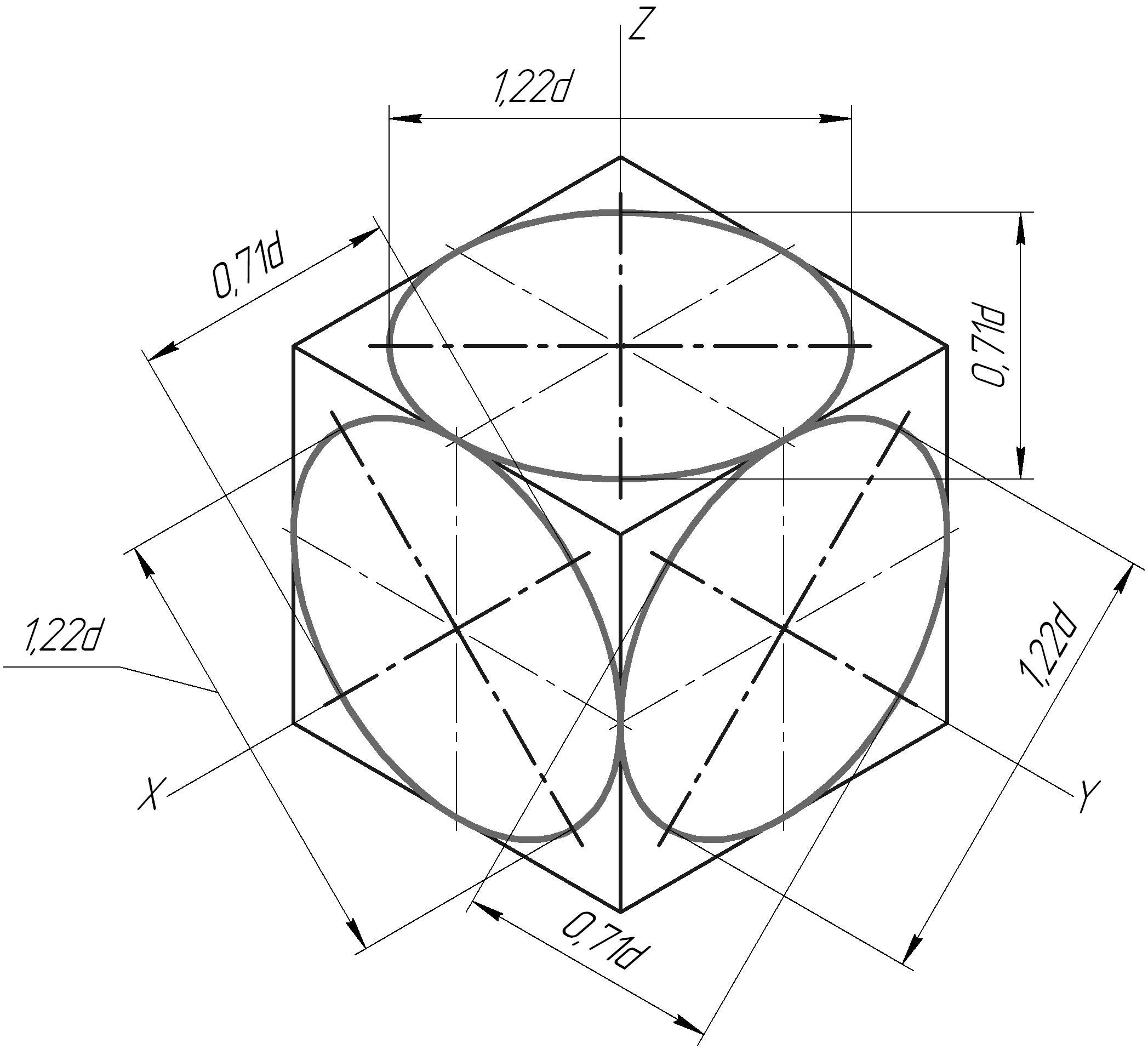
Рис. 5

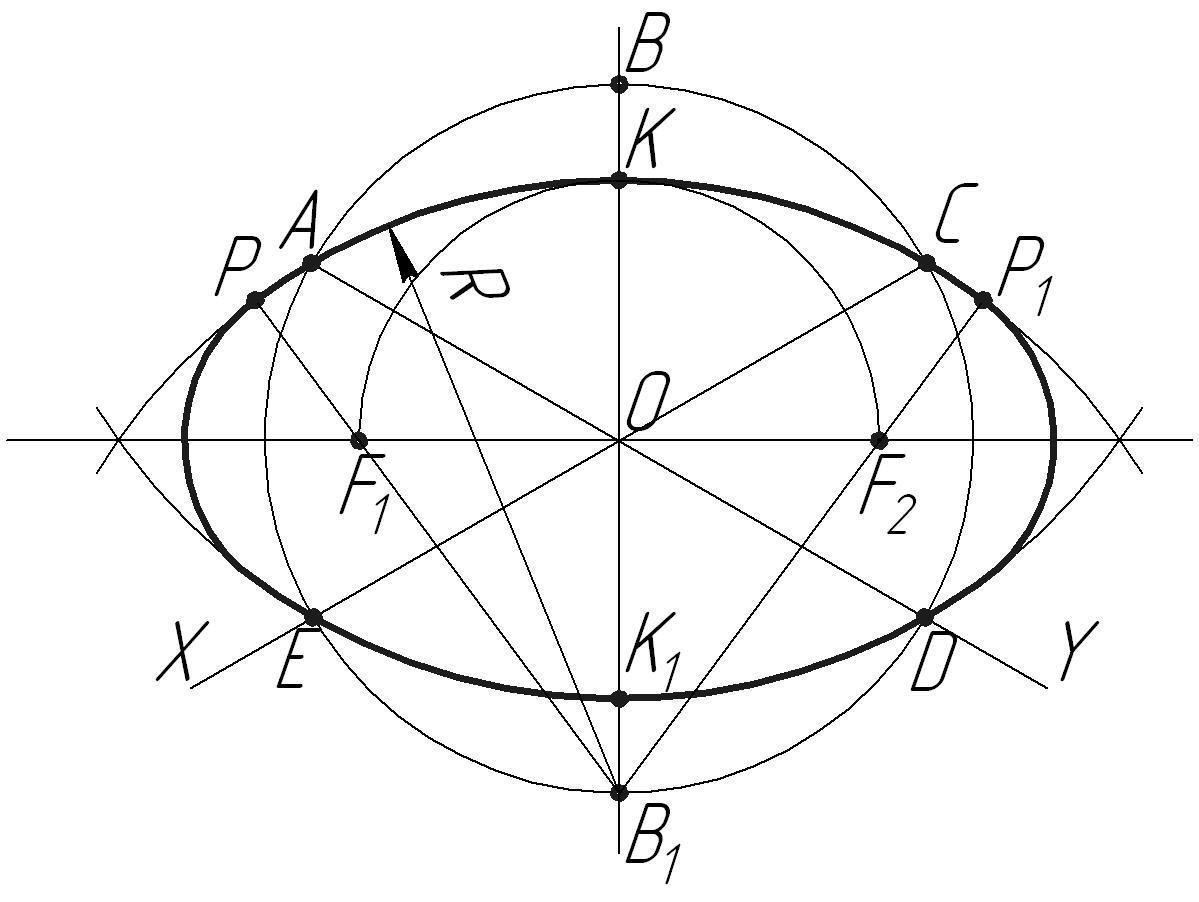
Рис. 6