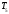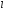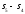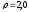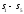Содержание
|
Задача №1 |
2 |
|
Задача №2 |
6 |
|
Задача №3 |
11 |
|
Задача №4 |
16 |
|
Список литературы |
20 |
Задача №1
В
процессе изменения состояния
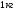 газа внутренняя энергия его увеличивается
на
газа внутренняя энергия его увеличивается
на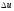 .
При этом над газом совершается работа,
равная
.
При этом над газом совершается работа,
равная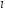 .
Начальная температура газа
.
Начальная температура газа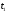 ,
конечное давление
,
конечное давление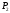 .
.
Определить
для заданного газа показатель политропы
 ,
начальные и конечные параметры, изменение
энтропии
,
начальные и конечные параметры, изменение
энтропии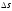 и изменение энтальпии
и изменение энтальпии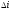
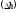 .
Представить процесс в
.
Представить процесс в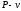 и
и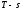 координатах. Изобразить здесь же (без
расчета) изобарный, изохорный,
изотермический и адиабатный процессы,
проходящие через начальную точку.
координатах. Изобразить здесь же (без
расчета) изобарный, изохорный,
изотермический и адиабатный процессы,
проходящие через начальную точку.

Решение:
Конечная температура процесса определяется из выражения для изменения внутренней энергии,
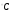 :
:
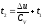 ,
,
где 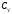 – удельная массовая теплоемкость в
процессе постоянного объема
– удельная массовая теплоемкость в
процессе постоянного объема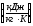 ,
вычисляемая из соотношения:
,
вычисляемая из соотношения:
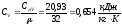 .
.
Конечная температура процесса равна:
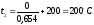 .
.
Показатель политропы определяется из выражения для работы процесса:
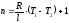 ,
,
где 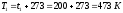 ;
;
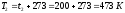 ;
;
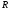 –постоянная
газовая постоянная,
–постоянная
газовая постоянная,
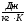 ,
определяемая выражением:
,
определяемая выражением:
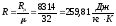 ,
,
где 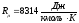 – универсальная газовая постоянная.
– универсальная газовая постоянная.
Показатель политропы равен:
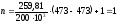 .
.
Так
как
 ,
то процесс изотермический.
,
то процесс изотермический.
Начальное давление газа можно найти из соотношения параметров изотермического процесса,
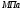 :
:
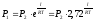 ;
;
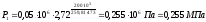 .
.
Начальный и конечный объем определяем из характеристического уравнения состояния газа,
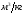 :
:
 ;
;
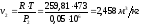 .
.
Изменение энтропии составит,
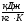 :
:
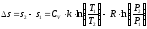 .
.
Или для изотермического процесса:
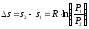
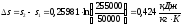 .
.
Изменение энтальпии процесса,
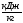 :
:
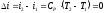 .
.
Для построения процессов в координатах
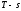 необходимо вычислить значение энтропии
газа в начальном состоянии по формуле,
необходимо вычислить значение энтропии
газа в начальном состоянии по формуле,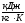 :
:
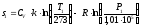 ,
,
где 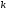 – показатель адиабаты, определяемый
зависимостью:
– показатель адиабаты, определяемый
зависимостью:
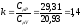 .
.
Значение энтропии газа в начальном состоянии равно:
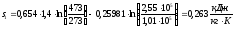 .
.
Изображение термодинамических процессов.
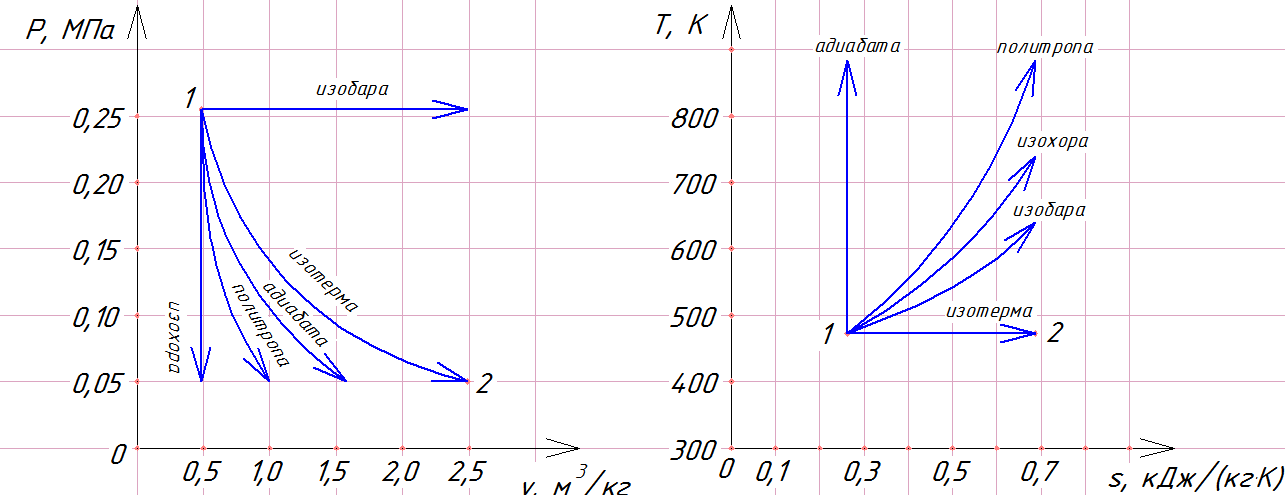
Задача №2
Определить
параметры рабочего тела в характерных
точках идеального цикла поршневого
двигателя внутреннего сгорания, если
известны давление
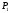 и температура
и температура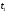 рабочего тела в начале сжатия.
рабочего тела в начале сжатия.
Степень
сжатия
 ,
степень повышения давления
,
степень повышения давления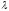 ,
степень предварительного расширения
,
степень предварительного расширения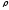 заданы.
заданы.
Определить работу, получаемую от цикла, его термический КПД и изменение энтропии отдельных процессов цикла.
За
рабочее тело принять воздух, считая
теплоемкость его в рабочих интервалах
температур постоянной, построить в
масштабе этот цикл в координатах
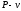 и
и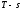 .
.
Исходные данные и искомые показатели
|
Дано |
Определить | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Удельный объем воздуха
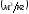 в точке 1 цикла, соответствующей
начальному состоянию, находится из
характеристического уравнения:
в точке 1 цикла, соответствующей
начальному состоянию, находится из
характеристического уравнения:
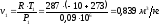 ,
,
где 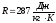 – индивидуальная газовая постоянная
воздуха.
– индивидуальная газовая постоянная
воздуха.
Так как сжатие происходит по адиабатному процессу, то параметры состояния рабочего тела в точке 2 цикла определяются выражениями:
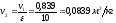 ;
;
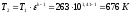 ,
,
где 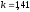 – показатель адиабаты для воздуха.
– показатель адиабаты для воздуха.
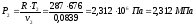 .
.
В процессе 2-3 цикла осуществляется изохорный подвод теплоты в количестве
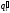 .
Исходя из этого, параметры рабочего
тела в точке 3 будут иметь следующие
значения:
.
Исходя из этого, параметры рабочего
тела в точке 3 будут иметь следующие
значения:
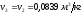 ;
;
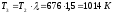 ;
;
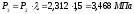 .
.
Линия 3-4 на диаграмме изображает изобарный процесс подвода теплоты в количестве
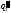 .
Исходя из условий изобарного процесса,
параметры рабочего тела в точке 4
составят:
.
Исходя из условий изобарного процесса,
параметры рабочего тела в точке 4
составят:
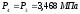 ;
;
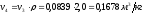 ;
;
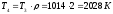 .
.
Дальнейший процесс расширения происходит по адиабате 4-5. Параметры состояния рабочего тела в точке 5 определяются выражениями:
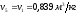 ;
;
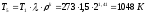 ;
;
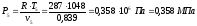 .
.
Количество подведенной теплоты в цикле составит:
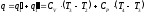 ,
,
где 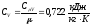 – удельная массовая теплоемкость
воздуха в процессе постоянного объема;
– удельная массовая теплоемкость
воздуха в процессе постоянного объема;
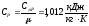 –удельная
массовая теплоемкость воздуха в процессе
постоянного давления.
–удельная
массовая теплоемкость воздуха в процессе
постоянного давления.
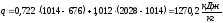 .
.
Отведенная теплота цикла (процесс 5-1) равна:
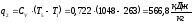 .
.
Полезная работа цикла составит:
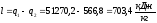 .
.
Термический КПД цикла равен
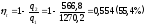 .
.
Изменение энтропии в процессах цикла определяется по формуле:
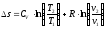 .
.
Адиабатные процессы 1-2 и 4-5:
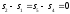 .
.
Изохорный процесс 2-3:
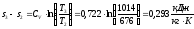 .
.
Изобарный процесс 3-4:
 .
.
Изохорный процесс 5-1:
 .
.
Проверка.
Для цикла должно быть:
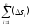 ,
,
где  – число участков цикла.
– число участков цикла.
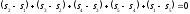 ;
;
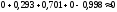 .
.
Следовательно, вычисления выполнены правильно.
Для построения цикла в координатах
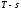 необходимо вычислить значение энтропии
газа в начальном состоянии по формуле:
необходимо вычислить значение энтропии
газа в начальном состоянии по формуле:
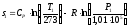 ;
;
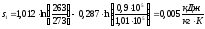 .
.
Расчетные данные для построения цикла ДВС.
Параметр
Координаты характерных точек цикла
1
2
3
4
5
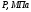
0,09
2,312
3,468
3,468
0,358
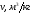
0,839
0,0839
0,0839
0,1678
0,839
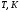
263
676
1014
2028
1048

0,005
0,005
0,298
0,999
0,999
Расчетная диаграмма термодинамического цикла ДВС со смешанным подводом теплоты (цикл Тринклера).
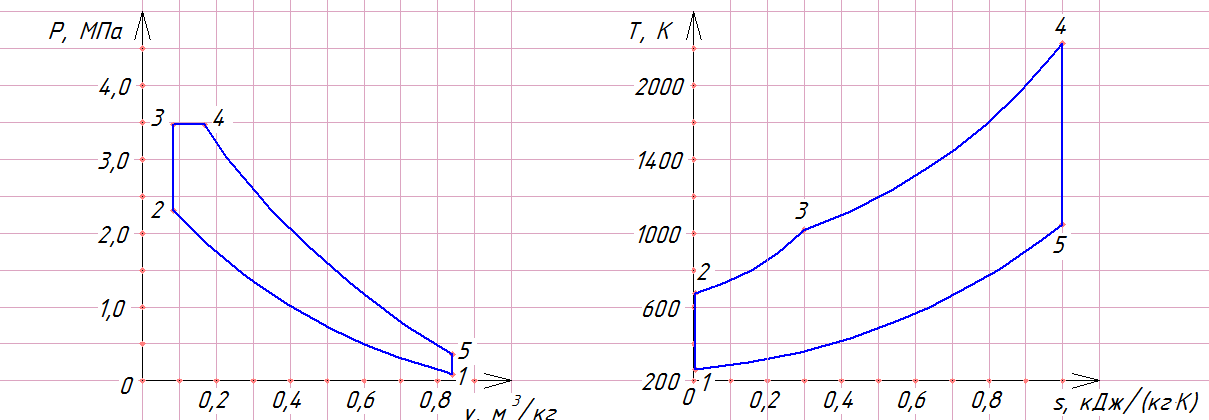
1-2 – сжатие;
2-3 – подвод теплоты в процессе расширения при постоянном давлении;
4-5 – расширение;
5-1 – выпуск ОГ при постоянном объеме.
Основные формулировки второго закона термодинамики.
Теплота не может самопроизвольно переходить от более холодного тела к более нагретому (формулировка Клаузиуса).
Вечный двигатель второго рода невозможен (формулировка Оствальда).
Там где есть разница температур возможно совершение работы (формулировка Карно).
Все самопроизвольные процессы в природе идут с увеличением энтропии.
При прохождении в изолированной системе самопроизвольных процессов энтропия системы возрастает (энтропия изолированной системы стремится к максимуму, так как самопроизвольные процессы передачи тепла всегда будут происходить, пока есть перепады температур).

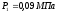
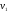 ,
,
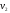 ,
,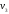 ,
,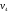 ,
,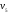
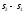
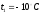
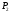 ,
,
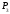 ,
,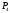 ,
,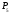
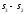
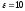
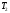 ,
,
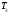 ,
, ,
,