уч.пос

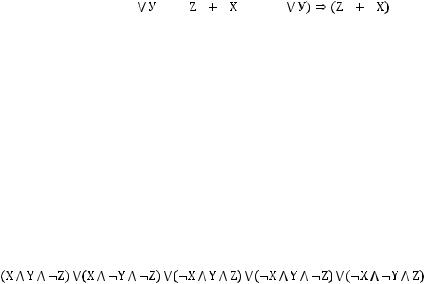
Задача №5. Привести пропозициональную форму к СДНФ:

(Х.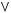

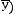
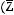
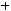
Варианты ответов:

1)(

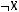
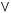
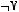
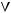
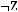
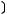
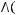
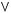
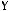
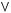
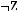
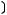
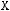
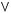
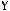
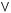
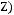
2)

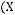
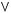
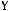
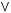
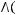
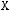
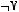
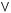
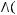
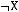
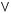
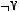
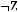
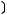
3)

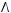
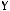
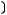
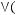
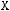
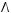
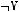
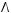
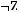
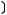
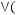
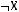
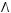
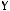
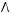
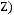
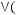
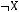
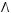
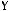
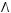
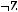
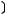
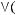
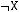
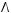
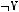
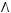
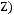
4)

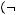
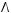
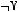
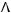
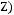
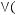
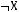
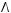
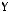
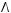
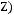
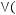
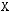
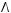
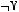
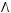
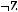
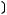
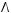
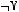
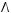
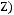
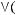
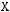
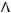
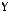
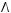
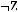
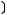
5)

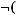
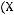
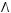
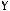
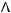
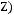
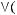
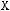
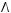
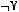
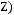
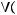
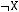
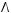
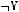
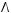
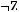
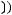
6)не существует

Решение:

Построим таблицу истинности для данной пропозициональной формы:

Для каждой строки таблицы, в которой получилось значение “истина”, построим соответствующую элементарную конъюнкцию.

2 строка: ;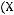

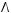
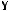
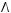
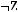
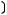4строка: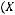

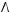
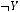
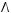
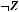
5строка: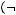

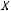
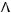
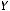
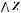
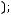
6строка: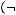

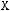
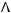
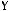
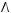
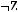
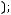
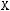
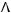
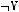
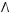
7строка: 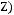. СДНФ:

Ответ: 3).

11

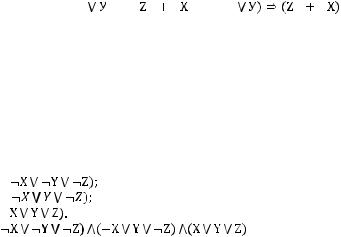
Задача №6. Привести пропозициональную форму к СКНФ:

(Х.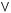

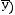
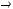
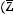
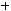
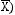Варианты ответов:

1)(

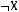
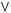
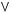
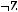
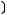
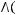
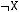
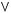
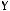
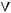
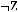
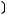
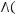
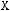
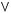
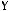
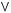
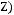
2)

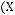
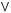
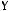
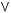
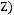
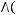
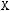
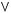
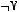
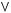
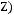
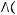
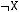
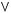
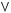
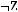
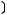
3)

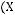
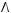
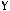
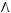
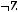
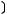
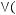
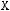
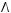
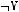
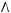
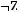
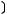
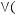
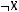
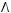
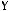
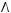
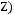
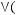
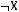
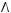
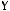
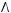
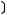
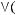
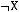
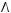
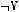
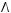
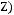
4)

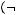
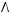
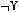
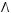
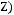
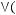
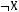
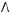
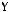
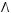
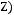
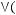
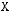
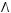
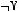
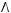
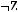
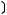
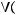
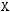
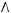
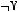
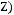
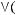
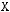
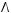
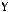
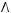
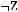
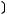
5)

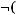
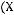
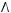
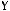
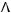
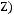
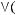
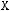
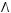
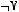
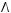
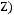
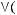
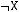
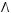
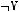
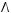
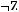
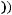
6)не существует

Решение:

Построим таблицу истинности для данной пропозициональной формы:

Для каждой строки таблицы, в которой получилось значение “ложь”, построим соответствующую элементарную дизъюнкцию.

Ответ: 1).

12

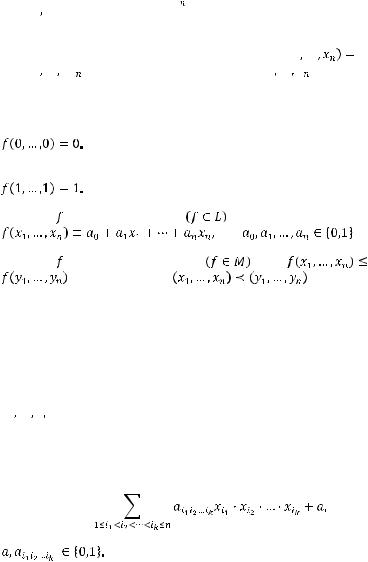
2. Булевы функции.

Теоретические сведения:i

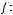
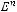
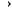
n-местной булевой функцией называется отображени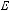е , где

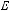
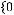
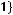. Всего существует 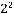булевых функций, зависящих от nпеременных.

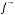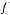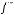
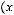
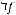
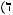
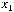
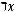
Функция называется двойственнойк, если 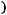для любых наборов значений .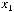

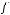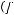
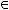
Функция называется самодвойственной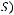, если .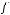

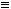
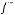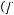
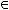
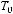
Функция называется функцией сохраняющей ноль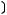, если

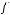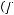
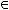
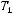
Функция называется функцией сохраняющей единицу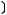, если

Система булевых функций называется полной, если любую булеву функцию можно получить как суперпозицию функций из этой системы. Система булевых функций называется базисом, если она полная, а любая ее подсистема полной не является.

Теорема Поста. Система булевых функций 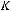является полной тогда и только тогда, когда система 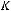не содержится ни в одном из классов:

.

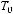
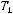
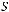
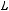
Многочленом Жегалкинаназывается многочлен, являющийся суммой константы и различных одночленов, в которых все переменные входят в степени не выше единицы:

13

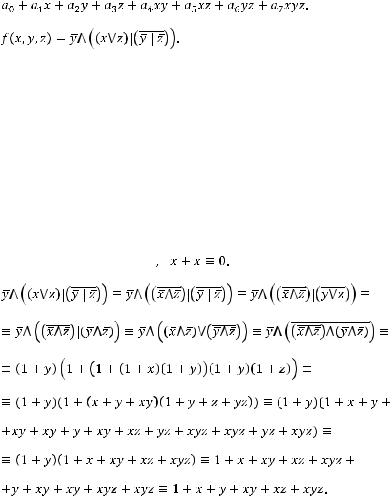
Теорема. Каждая булева функция единственным образом представляется многочленом Жегалкина.

Задача №7.Построить многочлен Жегалкина для данной булевой функции 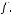Ввести последовательно без запятых коэффициенты многочлена

:

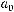
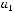
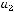
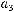
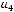
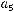
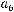
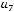Решение:

1 способ.

Воспользуемся алгоритмом:

1)Получить пропозициональную форму, эквивалентную исходной, но содержащую только связки ,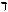

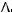
2)Заменить конъюнкцию на умножение, а отрицание - на прибавление единицы.

3)Раскрыть скобки и упростить полученную пропозициональную фор-

му, учитывая, что

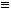
14

2 способ.

Получить СДНФ или СКНФ и преобразовать еѐ.

СДНФ: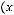

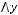
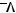
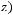
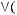
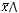
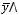
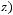
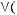
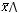
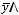
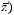
3 способ.

По значениям функции восстановить коэффициенты многочлена Жегалкина.

15

Ответ: 11101101.

Задача №8. Выбрать свойства, которыми обладает булева функция .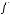

а) линейная;

б) самодвойственная;

в) сохраняет 0;

г) сохраняет 1;

д) монотонная;

е) не обладает ни одним из вышеперечисленных свойств.

Решение:

1) В предыдущей задаче мы получили многочлен Жегалкина для функции :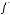

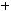
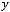
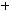
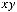
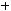
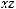
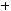
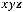. Следовательно, функция не яв-

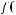
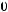
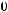
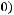
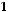
3) Функция не сохраняет 0.

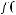
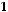
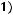
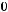
4) Функция не сохраняет 1.

16

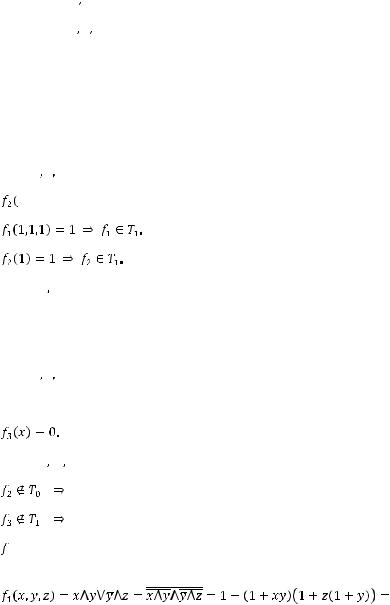
Задача №9. Исследовать на полноту систему булевых функций: .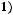

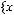
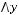
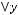
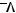
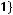2) .

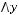
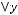
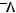
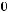
Варианты ответов:

а) полна;

б) не полна.

Решение:

1) .

.

.

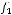
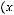
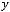
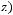
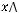
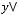
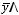
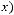
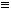
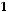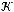
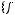
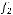
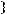
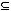
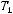По теореме Поста система 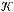не является полной.

Ответ: б).

2) .

.

.

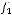
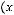
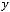
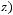
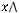
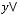
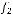
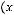
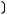
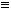
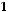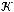
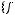
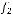
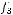
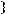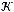не является подмножеством класса .

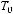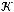не является подмножеством класса .

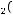
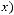
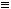
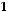
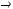
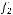
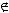
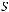
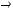
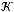не является подмножеством класса .

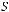17

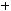
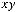
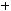
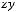
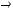
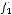
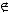
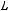
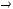
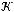не является подмножеством класса .

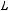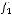
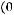
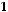
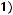
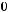
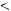
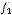
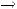
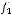
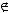
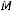
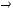
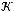не является подмножеством класса .

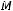По теореме Поста система 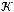является полной.

Ответ: а).

Задача №10. Исследовать на базисность систему булевых функций:

1);

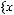
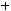
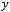
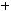
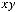
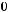
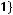2);

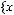
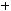
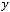
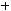
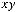
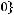3)

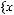
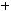
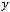
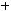
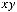
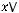
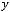
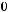
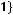
Варианты ответов:

а) базис;

б) не является базисом.

Решение:

1) .

.

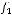
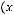
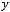
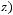
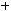
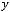
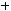
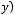
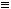
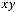Составим таблицу принадлежности функций из нашей системы классам

18

не содержит полных подсистем.

Следовательно, система является базисом.

Ответ: а).

2) .

.

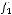
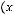
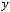
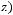
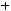
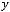
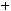
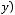
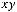Составим таблицу принадлежности функций из нашей системы классам

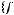
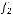
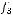
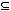
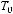. Следовательно, система не является полной, а значит, не является базисом.

Ответ: б).

19

3) .

.

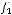
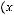
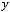
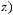
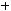
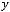
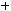
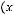
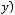
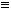
Составим таблицу принадлежности функций из нашей системы классам

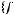
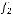
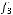
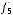
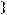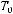
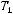
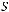
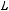
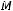
не содержится ни в одном из классов По теореме Поста система является полной.

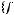
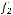
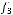
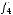
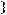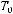
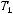
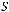
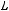
не содержится ни в одном из классов По теореме Поста эта подсистема является полной.

Следовательно, система не является базисом.

Ответ: б).

20