Ишниязова Эльвина

Ишниязова Эльвина

Вариант 9

1. Трое игроков A, B, C будут поочередно кидать монету. Выиграет тот, у кого появится герб. Обозначим: событие – у первого игрока при i -м бросании появится герб; – у второго игрока при i-м бросании появится герб; – у третьего игрока при i-м бросании появится герб. Используя алгебру событий, выразить события: A– выигрывает первый игрок; B – выигрывает второй; C – выигрывает третий – через события ,, .

Решение :

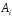_{- выигрывает 1-ый игрок}

_{- выигрывает 2 игрок}

_{- выигрывает 3 игрок}

A_i = A_i ++

B_i = + B_i +

C_i = ++

2. Из пяти букв разрезной азбуки составлено слово "книга". Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово "книга".

Решение:

n= p(5) = 5!

m = 1 ( число благоприятных исходов опыта)

p = = = =

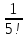3. Безотказная работа прибора определяется безотказной работой каждого из трех узлов, составляющих прибор. Вероятность безотказной работы за некоторый цикл соответственно равна , , . Найти вероятность безотказной работы прибора за указанный цикл.

p = p₁p₂ p₃ = 0.6 * 0.76 * 0.9 = 0.4104 ( решение по теореме умножения вероятностей )

4. Имеется 10 одинаковых урн, из которых в 9 находится по 2 черных и 2 белых шара, а в одном - 5 белых и 1 черный шар. Из взятой наудачу урны извлечен белый шар. Какова вероятность того, что этот шар извлечен из урны, содержащей 5 белых шаров.

Решение:

Выбор любой из 10 урн равновозможен, поэтому

По формуле полной вероятности.

- вероятность извлечения белого шара из первых девятых урн.

- вер-сть извлечения бел шар из десятой урны.

p = * 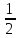+ * + * + * 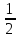+ * + * + * + * + * = вероятность того , что наугад выбранной урны будет извлечен белый шар

p = = * = = 0.156625

5. Дана функция плотности:

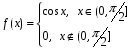
Найти функцию распределения и математическое ожидание .

Решение:

f(x)=