22). Геометрическое, гипергеометрическое распределения.

Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р       (О < р < 1) и, следовательно, вероятность его не появления q = 1 - р. Испытания заканчиваются, как только появится событие А (т.е. количество испытаний неограниченно). Таким образом, если событие А появилось в k-м испытании, то в предшествующих k—1 испытаниях оно не появлялось. Обозначим через X дискретную случайную величину -  число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: 1, 2, 3… Пусть в первых k—1 испытаниях событие А не наступило, а в k-миспытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,  Полагая k=1, 2, ... в формуле , получим геометрическую прогрессию с первым членом р и знаменателем q  ^ По этой причине распределение  называют геометрическим. Легко убедиться, что ряд  сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его : 

23). Распределения непрерывных случайных величин. Равномерное распределение.

Равномерное распределение. Непрерывная величина  Х  распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

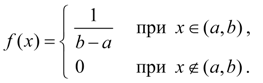            (29)

Для случайной величины Х , равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:

           (30) 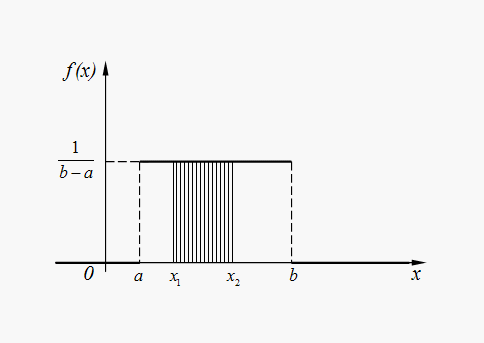  Рис. 4. График плотности равномерного распределения

 

Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда , то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале 

24). Распределения непрерывных случайных величин показательное, нормальное распределение.

Показательное распределение. Непрерывная случайная величина  Х  имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

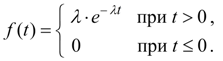          (31)

График плотности распределения вероятностей (31) представлен на рис. 5.

  Рис. 5. График плотности показательного распределения

 

Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ , физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.

Нормальное (гауссово) распределение. Случайная величина  Х  имеет нормальное (гауссово) распределение, если плотность распределения ее вероятностей определяется зависимостью:

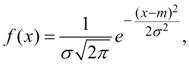            (32)

где m = M(X) , .

При   нормальное распределение называется стандартным.

График плотности нормального распределения (32) представлен на рис. 6.

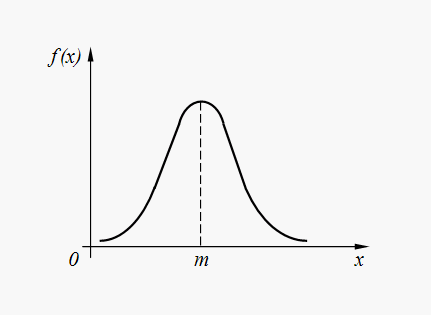  Рис. 6. График плотности нормального распределения

 

Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы.

-25). Системы случайных величин. Функция распределения. Совместная плотность распределения. Условные законы распределения.

Условным законом распределения величины , входящей в систему , называется ее закон распределения, вычисленный при условии, что другая случайная величина  приняла определенное значение .

Условный закон распределения можно задавать как функцией распределения, так и плотностью. Условнаяфункция распределения обозначается  условная плотность распределения .