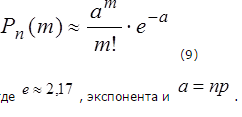17). Числовые характеристики случайных величин. Дисперсия. Свойства дисперсии.

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Свойства:

Дисперсия постоянной равна нулю: D(C)=0

  

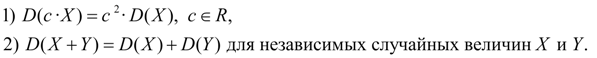
Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

D(X)=npq

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

18). Среднее квадратическое отклонение. Моменты. Асимметрия. Эксцесс.

Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х0называется математическое ожидание М ( Х – х0)k . Моменты относительно начала координат х = 0 называются начальными моментамии обозначаются:

         (12)

Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:

           (13)

Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:

          (14)

Из (7) следует, что центральный момент первого порядка всегда равен нулю:(15)

дисперсия  – это центральный момент второго порядка: (16)

Асимметрия. Центральный момент третьего порядка: (17)

служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным.

Эксцесс. Центральный момент четвертого порядка: (19)

служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения.

19). Вероятностный смысл математического ожидания.Свойства математического ожидания.

Математическое ожидание - это среднее значение случайной величины.

Математическим ожиданием дискретной случайной величины  Х , принимающей конечное число значений  хi   с вероятностями  рi , называется сумма:

  

Свойства математического ожидания:

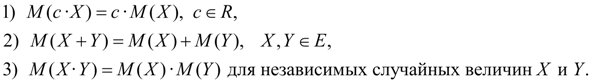
4)Математическое ожидание постоянной величины равно самой постоянной: М(С)=С

20). Распределения дискретных случайных величин. Биномиальное распределение.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимыхслучайных экспериментов, таких, что вероятность«успеха» в каждом из них постоянна и равна .

Биномиальным называют закон распределения дискретной случайной величины X- числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p, вероятность возможного значения X=k (числа k появлений события) вычисляют по формуле Бернулли: P_n(m) = C_n^mp^m q^{n – m}

21). Распределение Пуассона. Простейший поток событий.

Простейший поток событий

Стационарность. Это свойство означает, что вероятность попадания того или иного числа событий на временной интервалне зависит от того, где расположен этот участок, а зависит только от длины интервала, т. е. среднее число событий, появляющихся в единицу времени, постоянно. Обозначают его черези называютинтенсивностью потока.

Ординарность. Это свойство означает, что события возникаютпо одному. Поэтому ординарность потока выражается в том, что вероятность попадания на малый участокдвух и более событий пренебрежимо мала по сравнению с вероятностью попадания на него только одного события (это может быть только при малых). Другими словами, привероятность попадания на этот участок более одного события – бесконечно малая величина более высокого порядка малости, чем вероятность попадания на участок ровно одного события.

Отсутствие последействия. Свойство означает, что вероятность попадания того или иного числа событий на заданный участок осине зависит от того, сколько событий попало на любой другой, не перекрывающийся с ним участок. Иначе будущее потока не зависит от его прошлого.

Потоки, обладающие этими тремя свойствами, называются простейшими потоками событий. Простейший поток тесно связан с распределением Пуассона и поэтому часто называется стационарным пуассоновским потоком.

Простейший пуассоновский поток тесно связан с распределением Пуассона