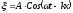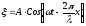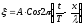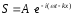- •Тема 5 (лекции 15-17): Волны План:
- •1. Волновые процессы. Упругие волны. Продольные и поперечные волны
- •2. Уравнение плоской и сферической волн
- •3. Уравнение бегущей волны
- •4. Принцип суперпозиции. Групповая скорость
- •5. Стоячие волны
- •6. Звук. Характеристики звука
- •7. Эффект Доплера в акустике
- •8. Дифференциальное уравнение электромагнитной волны
- •9. Энергия электромагнитной волны. Вектор Умова-Пойтинга
- •10. Излучение диполя
- •4. Шкала электромагнитных волн
Тема 5 (лекции 15-17): Волны План:
Волновые процессы. Упругие волны. Продольные и поперечные волны.
Уравнение плоской и сферической волн.
Уравнение бегущей волны.
Принцип суперпозиции. Групповая скорость.
Стоячие волны.
Звук. Характеристики звука.
Эффект Доплера в акустике.
Дифференциальное уравнение электромагнитной волны.
Энергия электромагнитной волны. Вектор Умова-Пойтинга.
Излучение диполя.
Шкала электромагнитных волн.
1. Волновые процессы. Упругие волны. Продольные и поперечные волны
Сплошная среда – непрерывно распределённая в пространстве среда, обладающая упругими свойствами.
Процесс распространения колебания в сплошной среде называется волновым процессам.
Основное свойство волны – перенос энергии без переноса вещества.
Упругими (механическими) волнами называют механические возмущения, распространяющиеся в упругой среде.
Волны, в которых частицы среды колеблются вдоль их распространения, называются продольными.

Волны, в которых частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны, называются поперечными.
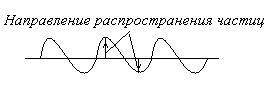
Продольные волны распространяются в жидкостях и газах
В твердой среде возникают как продольные, так ипоперечные
Упругая волна называется гармонической, если соответствующие колебания частиц среды являются гармоническими.
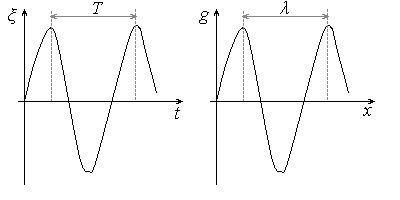
Длиной волны
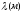 –
называют расстояние между ближайшими
точками, колеблющимися в одинаковой
фазе.
–
называют расстояние между ближайшими
точками, колеблющимися в одинаковой
фазе.
Формулы длины волны легко получить из аналогии по формуле пути:
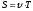
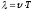
 – скорость волны
– скорость волны
Т – период колебаний


Геометрическое место точек, до которых доходит колебание к моменту времени t называется волновым фронтом.
Геометрическое место точек, колеблющихся в одинаковой фазе, называют волновой поверхностью.
2. Уравнение плоской и сферической волн
Уравнением волны называется выражение, которое даёт смещение колеблющейся частицы, относительно положения равновесия, как функцию её координат и времени.
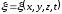 –уравнение волны
–уравнение волны

фаза = const


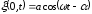

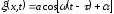 =
=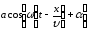
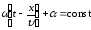
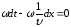
 –
фазовая
скорость
(скорость перемещения фазы)
–
фазовая
скорость
(скорость перемещения фазы)
Вывод:
скорость распространения волны есть
скорость
перемещения фазы волны,
поэтому ее называют фазовой
скоростью
и обозначают:
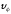 :
:
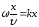 (
(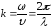 )
)
Т.к.
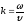 ,
отсюда
,
отсюда

|
Дисперсией называется зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой) |
Физический смысл
отношения
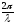 заключается в том, что оно показывает,
сколько длин волн умещается в
заключается в том, что оно показывает,
сколько длин волн умещается в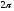 единицах длины. Отношение
единицах длины. Отношение обозначается
обозначается и называется волновым числом, т.е.
и называется волновым числом, т.е.
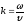
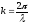
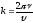

Например:
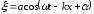 –
волна движется вдоль оси Ох
–
волна движется вдоль оси Ох
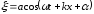 –
волна движется против оси Ох
–
волна движется против оси Ох
Для сферических колебаний:
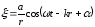 –без затухания
–без затухания
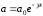 –закон затухания
–закон затухания
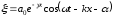 –затухающая
плоская волна
–затухающая
плоская волна
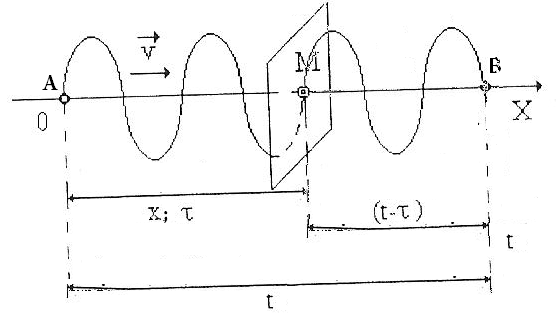
3. Уравнение бегущей волны
Бегущими волнами называют волны, которые переносят в пространстве энергию.

 ;
;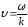

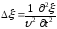 –
волновое уравнение
–
волновое уравнение
где
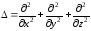 – оператор Лапласа
– оператор Лапласа
Для волны, распространяющейся вдоль оси Ох:
|
|
- первый вид уравнения плоской бегущей волны | |
|
|
- второй вид уравнения плоской бегущей волны | |
|
|
- третий вид уравнения плоской бегущей волны | |
|
|
- четвертый вид уравнения плоской бегущей волны | |
|
|
|
- уравнения плоской бегущей волны в комплексном виде
|
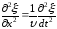
Итак: