Дифференциальные уравнения Основные понятия

Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.

Общий вид дифференциальных уравнений: F (x,y,y’,y’’..y’’’) = 0

Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения.

Процесс отыскания решения ДУ называется его интегрированием.

Дифференциальные уравнения первого порядка

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида F(x, y, y' )=0, где F — известная функция трех переменных, x — независимая переменная, y(x) — искомая функция, y'(x) — ее производная.  Если уравнение F(x, y, y' )=0 можно разрешить относительно y', то его записывают в виде y'=f(x, y)

Уравнение y'=f(x, y) устанавливает связь между координатами точки (x, y) и угловым коэффициентом y' касательной к интегральной кривой, проходящей через эту точку.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

P(x;y)dx+Q(x;y)dy=0,

Где P(x;y) и Q(x;y) – известные функции. Уравнение P(x;y)dx+Q(x;y)dy=0 удобно тем, что переменные в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.

 

Если дифференциальное уравнение первого порядка y'=f(x, y), имеет решение, то   решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=φ(x,C), где C — произвольная константа.

Функция y=φ(x,C) называется общим решением дифференциального уравнения 1-го порядка. Она содержит одну произвольную постоянную и удовлетворяет условиям:

1. Функция y=φ(x,C) является решением ДУ при каждом фиксированном значении С.

2. Каково бы ни было начальное условие y(x₀)= y₀, можно найти такое значение постоянной С=С₀ , что функция y=φ(x,C₀) удовлетворяет данному начальному условию.

Частным решением ДУ первого порядка называется любая функция y=φ(x,C₀), полученная из общего решения y=φ(x,C) при конкретном значении постоянной С=С₀ .

Задача отыскания решения ДУ первого порядка P(x;y)dx+Q(x;y)dy=0, удовлетворяющего заданному начальному условию y(x₀)= y₀ , называется задачей Коши.

Теорема(существования и единственности решения задачи Коши).

Если в уравнении y'=f(x, y) функция f(x, y) и ее частная производная f'_y(x, y) непрерывны в некоторой области D, содержащей точку (x₀ ; y₀ ), то существует единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию y(x₀)= y₀ . (без доказательства)

Уравнения с разделяющимися переменными

Наиболее простым ДУ первого порядка является уравнение вида

P(x)dx+Q(y)dy=0.

В нем одно слагаемое зависит только от x, а другое - от y. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:

∫ P(x)dx+∫Q(y)dy=с – его общий интеграл.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:

P₁(x) ^. Q₁(y) ^. dx+ P₂(x) ^. Q₂(y) ^. dy=0.

Особенность этого уравнения в том, что коэффициенты представляют собой произведения двух функций, одна из которых зависит только от х другая – только от у.

Уравнение P₁(x) ^. Q₁(y) ^. dx+ P₂(x) ^. Q₂(y) ^. dy=0 легко сводится к уравнению P(x)dx+Q(y)dy=0. путем почленного деления его на Q₁(y) ^. P₂(x)≠0. Получаем:

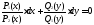, - общий интеграл.